Study on risk prediction of mine karst collapse under the influence of groundwater based on LOF-SMOTE algorithm
-
摘要: 矿山岩溶地表塌陷成因复杂，形式多样，为准确预测矿山岩溶塌陷，结合岩溶发育机理，本研究提出基于LOF和SMOTE算法的BP神经网络预测模型。首先通过LOF算法剔除因非自然原因而产生的异常数据，再通过SMOTE算法对剔除后的数据进行过采样，合成新数据，以增加样本数目，最后采用BP神经网络模型对矿山岩溶塌陷进行预测。结果表明，实际工程数据经过预处理后的预测模型，与部分小样本预测模型相比，具有更高的预测精度，可为在其他工程中应用提供参考。Abstract: The causes of mine karst surface collapse are complex and diverse. To accurately predict karst collapse in mines, combined with the karst development mechanism, a BP neural network prediction model based on the LOF and SMOTE algorithms is proposed. In this model, the abnormal data due to unnatural reasons were first removed by LOF algotithm. The removed data were then oversampled by SMOTE algorithm, thereby synthesizing new data to increase the number of samples. Finally, the BP neural network model was used to predict the mine karst collapse. The results show that the preprocessed prediction model of the actual engineering data has higher prediction accuracy than some small sample prediction models, which provides a reference for its application in other projects.
-
Keywords:
- karst collapse /
- LOF algorithm /
- SMOTE algorithm /
- neural network /
- support vector machine
-
岩溶塌陷是矿山地表塌陷的原因之一，是一种常见的矿山地质灾害[1]。岩溶塌陷不但影响企业效益及生态环境，更对相关领域工作人员生命安全带来威胁，因此，准确预测岩溶塌陷现象具有极大的实际意义。
为对岩溶塌陷进行准确预测，首先需要了解岩溶发育和塌陷的影响因素。有关岩溶发育机理及影响因素的多项研究[2-11]表明，岩溶主要由可溶岩与地下水相互作用而产生，其主要原理是水、二氧化碳与可溶岩中的碳酸成分发生的化学反应。岩溶塌陷是岩溶结构导致的塌陷现象，是多因素叠加的结果[12-16]。岩溶塌陷一般发展过程是，地下水对可溶性基岩侵蚀产生岩溶构造，岩溶构造上的覆盖土由于受地下水的动力影响产生土洞，随着土洞不断扩大，地表随之塌陷。石树静等[17]认为岩溶塌陷是多种不良因素共同作用的产物，其致塌因素主要包括特殊的“水-土-岩”组合及人为活动；也有研究表明地下和地表水体对土层的潜蚀作用导致岩溶地面塌陷[18-22]。结合土的本质作用，根据不同类型的覆盖层，可将塌陷分为土洞型、沙漏型和泥流型3种塌陷机制[23-24]。因此，预测模型中的评价指标应以相关影响因素为参考进行选取。
研究者采用多种方法实现岩溶塌陷的预测。例如，使用模糊综合评价法预测岩溶塌陷[25-26]，但模型在指标权值的确定过程中，不同程度地使用了专家打分法，理论上仍具有一定的主观性。PERRIN等[27]根据塌陷发育的影响因素及过程，分析权重后建立了岩溶塌陷敏感性模型，具有一定的效果，但在具体应用中，对于岩溶塌陷不集中区域仍有20%无法预测，在这类区域中的预测效果差强人意。YAU等[28]结合数值模拟方法提出了一种概率模型预测岩溶空腔分布，取得了预期结果，但模型在建立和运行时比较耗时。综上可知，因实际工程中的现象是复杂的，在使用传统评价方法时难以避免繁琐且带有一定主观性的过程，导致传统评价方法在一些工程条件下具有一定的局限性。
神经网络模型能够根据训练样本自动调整结构参数，改变映射关系，具有较强的自适应性，可实现多种非线性映射，较好地解决了传统方法中主观性大的问题，提高评估精确性，简化过程。BP神经网络是一种经典的神经网络模型，已被证实在岩溶塌陷预测问题中具有一定的实用性[29-32]，并且在部分工程中也取得了较好的效果。但是，神经网络预测模型在使用时对样本数量具有一定的要求，工程数据数量主要由工程需求决定，样本数量过少会过拟合，导致预测效果不良，并且受环境、人员等因素影响，使得样本数量及质量无法满足模型学习需求，达不到预期的效果。
LOF（Local Outlier Factor）算法可将样本数据中异常（离群）数据检测并剔除，SMOTE（Synthetic Minority Oversampling Technique）算法可合成新的少数类样本，均衡样本种类。在类似的工程问题中，谭文侃等[33]采用LOF算法和SMOTE算法组合对强烈岩爆进行了预测，结果表明，经过改进方法处理后，有效且可靠地提高了机器学习的岩爆预测模型准确率。本文采用LOF算法及SMOTE算法对工程数据进行预处理，依据岩溶塌陷机理建立BP（Back Propagation）神经网络岩溶塌陷风险预测模型。
1 模型基本原理
1.1 LOF算法
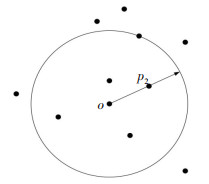
LOF算法[34]是一种基于密度无监督的局部离群点检测方法，可计算数据点相对于其邻域的局部密度偏差，通过对比确定数据对象的离群值。其主要步骤如下：
1）k距离邻域
数据点p的邻域Nk(p)到数据点p的距离小于等于点p第k距离的点的集合，即：
(1) 
(2) 当dk(p) =d(p, o)时需满足：
① 数据集D中至少有不包括p的k个点
② 数据集D中至多有不包括p的k-1个点
2）可达距离
点o至点p第k可达距离
(3) ![]()
图 1 当k=5时，点o至点p1的可达距离示意Figure 1. Schematic diagram of accessible distance from point o to point p1 when k=5![]()
图 2 当k=5时，点o至点p2的可达距离示意Figure 2. Schematic diagram of accessible distance from point o to point p2 when k=53）局部可达密度
局部可达密度可由点p的第k邻域内点到p的平均可达距离的倒数表示，密度越低，离群点的可能性越大，表达式如下：
(4) 4）局部离群因子
局部离群因子是点p的邻域内所有点的平均局部可达密度与点p本身的局部可达密度之比的平均值，表达式如下：
(5) 若局部离群因子的值越大于1，说明p的密度越小于邻域的平均密度，该点可能是一个离群点。
1.2 SMOTE算法
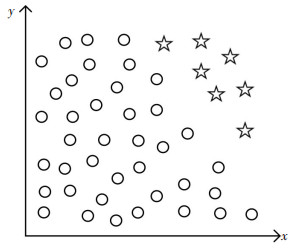
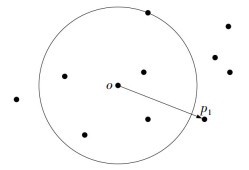
SMOTE算法的主要思路是以少数类样本为基础合成新的样本[35]，在此过程中不但可以控制新样本的数量，还可以限制新样本的分布区域[36]。以图 3样本示意图为例，其中，圆形代表多数类样本，星形代表少数类样本。
![]()
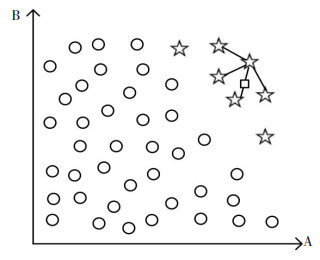
图 3 样本示意（其中星形为少数类样本）Figure 3. Schematic diagram of sample (the stellate ones are a minority of class samples)对于少数类样本，以欧式距离为标准计算其到同类样本的距离，得到k近邻。少数类样本中选择一个点xo，从其k近邻随机选择某点xp，根据式（6）得到新样本x'。图 4中方形为星形合成的新样本。
![]()
图 4 新样本示意（其中方形为新合成样本）Figure 4. Schematic diagram of new sample (the square ones are new synthetic samples)
(6) 1.3 BP神经网络
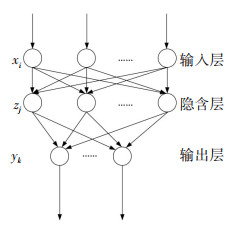
BP神经网络是一种输入信号正向传播，误差反向传播的神经网络模型。通过学习训练对某项结果进行预测，根据预测结果与预期结果的误差修改权值和阈值，进一步调整使其与预期结果一致。图 5所示为BP神经网络示意图，BP神经网络由输入层、隐含层和输出层组成。
BP神经网络训练步骤主要有以下步骤:
① 确定输入输出值，输入、隐含、输出节点数，初始化不同层间权值ωji、νkj。
② 计算隐含层输出，计算公式如式（7）所示，其中，θj为隐含层节点，j为隐含层节点数，f为传递函数。
(7) ③ 计算输出层输出，计算公式如式（8）所示，其中，φk为输出层阈值(k为输出层节点数)。
(8) ④ 根据Ok及y计算网络预测误差e。
⑤ 根据误差e使用式（9）和式（10）调整权值，使用式（11）和式（12）调整阈值。
(9) 
(10) 
(11) 
(12) ⑥ 检验目标误差。
2 模型建立
2.1 评价指标的确定
杨彪[37]根据某矿山岩溶地表塌陷实测数据，确定了地下水、水文地质参数、覆盖层、环境、岩性这5个方面岩溶塌陷影响因素，以及12个显著影响岩溶地表塌陷的子因素，因研究区基岩地层均为壶天群含水层，因此不考虑地层岩性的影响，所以选取11个因子作为评价指标，分别为地下水位（x1）、地下水位波动幅度（x2）、给水度（x3）、横向渗透系数（x4）、纵向渗透系数（x5）、贮水系数（x6）、覆盖层厚度（x7）、人工抽水强度（x8）、河流和湖泊（x9）、降雨量（x10）和井下涌水点含沙率（x11）。同时，将5个方面的因素按照对岩溶地表的影响不同程度的进行了量化分级，如表 1—表 6所列，以此为基础将最终预测期望输出参数分为5级，如表 7所列。本文将采用该文献确定的指标、数据及分级。
表 1 地下水影响量化分级表Table 1. Quantified grading table of groundwater impact表 2 覆盖层影响量化分级表Table 2. Quantitative grading table of overburden impact表 3 降雨量影响量化分级表Table 3. Quantitative grading table of rainfall impact表 4 河流湖泊影响量化分级表Table 4. Quantitative grading table of river and lake impact表 5 矿坑涌水量影响量化分级表Table 5. Quantitative classification table of mine water inflow effect表 6 井下涌水点含沙率影响量化分级表Table 6. Quantitative grading table of influence of sand content at underground water gushing point表 7 期望输出参数分级Table 7. Expected output parameter grading地下水对岩溶地表塌陷的影响主要体现在地下水位和地下水位波动幅度两个因素上。依据矿山工程实际进行量化分级，如表 1所列。
研究区地表覆盖着第四系粉质黏土和粉土夹砂砾石厚度为10~30 m，含水性能弱，降雨通过覆盖层进入含水层。覆盖层厚度是影响地表塌陷的重要因素，依据矿山工程实际进行量化分级，如表 2所列。
该矿曾为了消除地下水对井下开采的影响，建设了截流疏干系统，降低了整个地区的水位，形成较大水力坡度。通过监测矿坑涌水量和井下涌水点含沙量反映抽水强度对塌陷的影响，因此根据矿山工程实际进行量化分级，如表 3—表 6所列。
2.2 训练及预测
采用Python语言对样本进行预处理，采用LOF算法对岩溶塌陷数据集进行检测，剔除离群点，之后由SMOTE算法过采样，各类样本总数由原21组增加到436组，并从原数据及新合成数据中分层抽样后增加训练集与测试集。表 8所示为原训练样本，表 9所示为原预测样本。
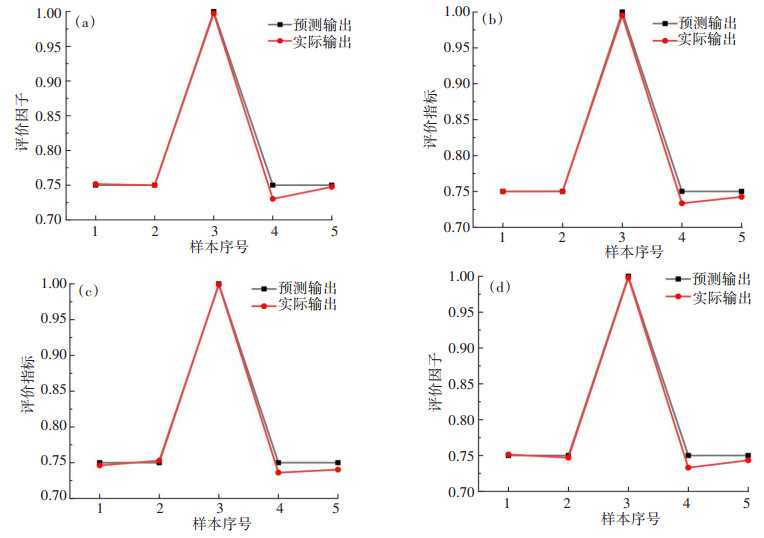
表 8 原训练样本Table 8. Original training samples表 9 原预测样本Table 9. Original prediction samples根据预处理后的训练集与测试集，建立BP神经网络预测模型，其中，参数设置中目标误差0.000 1，步数2 000，输入节点11个，学习率为0.01。在训练和预测时，采取随机10组的结果求平均值的方法减少样本误差。图 6（a）、图 6（b）、图 6（c）为节选3组预测结果，图 6（d）为10组平均预测结果，表 10为预测结果。
![]()
图 6 预测结果：（a）、（b）、（c）为节选的3组预测结果；（d）为10组平均预测结果Figure 6. Prediction results: (a), (b) and (c) are three prediction groups of results excerpted; (d) is the average prediction result of ten groups表 10 预处理后实际输出与预测结果对比Table 10. Comparison between the actual output results after pretreatment and predicted results2.3 预测分析
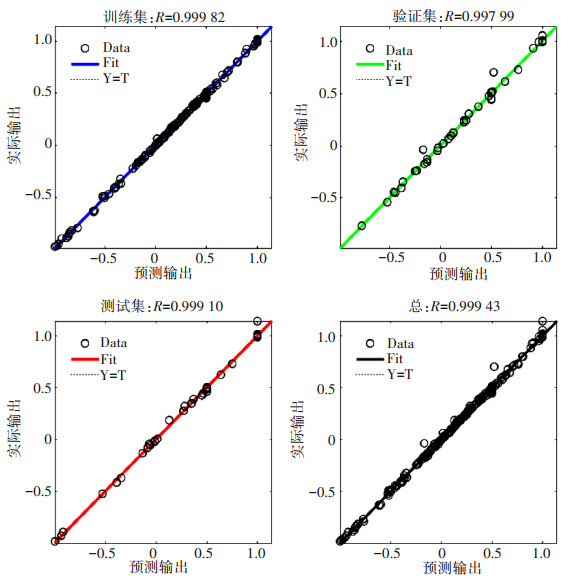
参考文献[38]根据本文中预处理前的原始数据，使用PCA-PSO-SVM方法对矿山岩溶塌陷进行预测，取得了较好的预测效果见表 10。表 11将本文模型预测误差与文献[38]的模型误差做对比，本文模型的预测相对误差分别0.20%、-0.41%、-0.20%、-2.26%、-0.90%，均优于SVM预测模型的8.93%、10.00%、-3.40%、3.20%、5.20%，基本优于PCA-PSO-SVM预测模型的2.00%、3.07%、-1.10%、0.13%、4.27%，结合样本回归情况（图 7），其中，回归值R表示实际与预测之间的相关性，R越接近1表示关系越密切，可以看出各类数据都呈现出较好的回归性，进一步说明了在相对满足神经网络对于样本数量的需求下，LOF-SMOTE-BPNN预测模型对于预测岩溶塌陷问题具有较高的使用价值。
表 11 3种预测模型误差对比Table 11. Error comparison of three prediction models![]()
图 7 样本回归情况（回归值R表示实际与预测之间的相关性，越接近1表示关系越密切）Figure 7. Sample regression (the regression value R represents the correlation between actual and forecast, and the closer it is to 1, the closer the relationship is)2.4 应用案例
本文根据某矿山工程实例建立了LOF-SMOTE-BPNN模型，并与同工程条件下其他预测模型的效果进行了对比，取得了较好的预测效果。因模型基于岩溶塌陷原理，所以其不但适用于矿山岩溶塌陷预测，还可用于其他岩溶塌陷工程预测。根据桂林市内岩溶塌陷问题[31]，应用LOF-SMOTE-BPNN模型进行预测，并与实际结果作对比，验证模型的准确性与实用性。
文献[31]统计了桂林市40余年发生的200余起岩溶地面塌陷，从近200个岩溶塌陷的实例中抽出14个样本，根据岩溶地面塌陷的诱发因素，选取了岩性系数（RQC）、岩体结构系数（RMSC）、地下水系数（GWC）、覆盖层系数（SSC）、地形地貌系数（LPC）、环境条件系数（ECC）6个评价因素，将岩溶地面塌陷程度由稳定到很易塌陷分为A、B、C、D、E五级状态。将五级状态赋予阈值1~5进行预测[39]，根据其中的训练预测样本中C级样本，验证模型可靠性。表 12为C级样本评价指标。
表 12 C级样本评价指标Table 12. Evaluation indexes of grade C samples表 13为C级3号样本未预处理与预处理后预测结果对比，由于原始数据中C级样本数量较少，训练不够充分，预测结果为B级与实际情况不相符，经过预处理后的预测结果为C级与实际情况一致，模型对小样本C级预测效果显著提升。
表 13 C级3号样本未预处理与预处理后预测结果对比Table 13. Comparison between the prediction results of grade C No.3 sample without pretreatment and after pretreatment3 结论
1）本文采用LOF与SMOTE算法，对矿山地表岩溶塌陷原始数据进行预处理，剔除了离群数据后增加了少数类样本，基本满足了神经网络模型对于样本数量的要求，提高了模型预测效果。
2）数据预处理后的BP神经网络模型，预测相对误差分别为0.20%、-0.41%、-0.20%、-2.26%、-0.90%，精度较高，具有较好的预测能力，因此LOF-SMOTE-BPNN可为小样本矿山岩溶塌陷预测提供思路，并为矿山岩溶塌陷治理提供依据。
3）以桂林岩溶地面塌陷实例中C级岩溶塌陷程度为例，对模型进行验证，预测结果与实际情况一致，进一步证明了模型的可行性。
-
![]()
图 1 当k=5时，点o至点p1的可达距离示意
Fig 1. Schematic diagram of accessible distance from point o to point p1 when k=5
![]()
图 2 当k=5时，点o至点p2的可达距离示意
Fig 2. Schematic diagram of accessible distance from point o to point p2 when k=5
![]()
图 3 样本示意（其中星形为少数类样本）
Fig 3. Schematic diagram of sample (the stellate ones are a minority of class samples)
![]()
图 4 新样本示意（其中方形为新合成样本）
Fig 4. Schematic diagram of new sample (the square ones are new synthetic samples)
![]()
图 6 预测结果：（a）、（b）、（c）为节选的3组预测结果；（d）为10组平均预测结果
Fig 6. Prediction results: (a), (b) and (c) are three prediction groups of results excerpted; (d) is the average prediction result of ten groups
![]()
图 7 样本回归情况（回归值R表示实际与预测之间的相关性，越接近1表示关系越密切）
Fig 7. Sample regression (the regression value R represents the correlation between actual and forecast, and the closer it is to 1, the closer the relationship is)
表 1 地下水影响量化分级表
Table 1 Quantified grading table of groundwater impact
表 2 覆盖层影响量化分级表
Table 2 Quantitative grading table of overburden impact
表 3 降雨量影响量化分级表
Table 3 Quantitative grading table of rainfall impact
表 4 河流湖泊影响量化分级表
Table 4 Quantitative grading table of river and lake impact
表 5 矿坑涌水量影响量化分级表
Table 5 Quantitative classification table of mine water inflow effect
表 6 井下涌水点含沙率影响量化分级表
Table 6 Quantitative grading table of influence of sand content at underground water gushing point
表 7 期望输出参数分级
Table 7 Expected output parameter grading
表 8 原训练样本
Table 8 Original training samples
表 9 原预测样本
Table 9 Original prediction samples
表 10 预处理后实际输出与预测结果对比
Table 10 Comparison between the actual output results after pretreatment and predicted results
表 11 3种预测模型误差对比
Table 11 Error comparison of three prediction models
表 12 C级样本评价指标
Table 12 Evaluation indexes of grade C samples
表 13 C级3号样本未预处理与预处理后预测结果对比
Table 13 Comparison between the prediction results of grade C No.3 sample without pretreatment and after pretreatment
-
[1] 管佳林, 罗周全, 杨彪, 等. 矿区岩溶地表塌陷神经网络预测模型研究[J]. 中国安全科学学报, 2011, 21(9): 28-33. doi: 10.3969/j.issn.1003-3033.2011.09.005 [2] STRINGFIELD V T, RAPP J R, ANDERS R B. Effects of Karst and geologic structure on the circulation of water and permeability in carbonate aquifers[J]. Journal of Hydrology, 1979, 43(1/2/3/4): 313-332.
[3] 罗小燕, 黄祥海, 汤文聪. 基于改进VMD和GA-BP神经网络的砂岩破裂过程预测方法[J]. 有色金属科学与工程, 2021, 12(1): 99-107. doi: 10.13264/j.cnki.ysjskx.2021.01.013 [4] 卢耀如. 中国南方喀斯特发育基本规律的初步研究[J]. 地质学报, 1965, 39(1): 108-129. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXE196501008.htm [5] 任美锷, 刘振中, 王飞燕, 等. 中国岩溶发育规律的若干问题[J]. 南京大学学报(自然科学版), 1979, 15(4): 95-108. https://www.cnki.com.cn/Article/CJFDTOTAL-NJDZ197904011.htm [6] 罗小杰. 武汉地区浅层岩溶发育特征与岩溶塌陷灾害防治[J]. 中国岩溶, 2013, 32(4): 419-432. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201304009.htm [7] 官善友, 蒙核量, 周淼. 武汉市岩溶分布与发育规律[J]. 城市勘测, 2008(4): 145-149. doi: 10.3969/j.issn.1672-8262.2008.04.044 [8] 罗书文, 杨桃, 邓亚东, 等. 桂林岩溶地貌发育演化过程地文期的解析研究[J/OL]. 地质通报, 1-16[2022-05-08]. http://kns.cnki.net/kcms/detail/11.4648.p.20220304.1708.002.html. [9] 肖华, 张传英, 王彦明, 等. 嘉祥县红运水源地岩溶发育特征及富水规律研究[J]. 山东国土资源, 2021, 37(7): 44-48. https://www.cnki.com.cn/Article/CJFDTOTAL-SDDI202107008.htm [10] 董崇能. 大板桥-长水机场一线岩溶发育规律研究[D]. 昆明: 昆明理工大学, 2021. [11] 周宇成, 陈清华, 孙珂, 等. 湖南地区岩溶分布特征及其发育模式[J]. 中国石油大学学报(自然科学版), 2020, 44(4): 163-173. https://www.cnki.com.cn/Article/CJFDTOTAL-SYDX202004020.htm [12] CURRENS J. Hypothesized mechanism for the initiation of soil caviries and subsequent cover collapse in Karst terrain[J]. Journal of Cave and Karst Studies, 2018, 80(4): 172-180. doi: 10.4311/2016ES0148
[13] 王飞, 柴波, 徐贵来, 等. 武汉市岩溶塌陷的演化机理研究[J]. 工程地质学报, 2017, 25(3): 824-832. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201703030.htm [14] 张晓斌. 福建省大田县桃源镇前厝村岩溶塌陷发育特征及成因分析[J]. 地质灾害与环境保护, 2018, 29(4): 15-20. https://www.cnki.com.cn/Article/CJFDTOTAL-DZHB201804003.htm [15] 陈亮晶, 孙锡良, 皮景, 等. 湖南宁乡大成桥地区岩溶地面塌陷分布特征及影响因素分析[J]. 中国岩溶, 2014, 33(4): 490-497. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201404015.htm [16] 魏永耀, 孙树林, 黄敬军, 等. 徐州岩溶塌陷时空分布规律及成因分析[J]. 中国岩溶, 2015, 34(1): 52-57. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201501007.htm [17] 石树静, 张勤军, 康志强. 南宁市坛洛镇岩溶塌陷群成因机制分析[J]. 中国岩溶, 2015, 34(5): 507-514. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201505011.htm [18] 吴永华, 谢春波, 朱洵. 陆家街地区岩溶塌陷形成机制及预测评价[J]. 中国地质灾害与防治学报, 1994, 5(增刊1): 118-123. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH4S1.018.htm [19] 周关学, 冯涛, 张广泽. 柳南铁路凤凰至来宾段地面塌陷机理及防治措施研究[J]. 公路工程, 2019, 44(4): 232-238. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGL201904042.htm [20] 郑智, 简文彬. 龙岩市岩溶塌陷地质结构及其致塌机理[J]. 地质灾害与环境保护, 2017, 28(4): 38-43. https://www.cnki.com.cn/Article/CJFDTOTAL-DZHB201704009.htm [21] 李颜贵, 刘子龙, 于孝民, 等. 唐山黄庄岩溶塌陷形成条件和机理分析[J]. 中国岩溶, 2014, 33(3): 299-307. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201403007.htm [22] 邢宇健. 岩溶区地下水位动态变化诱发地表塌陷的机理研究[D]. 北京: 北京交通大学, 2018. [23] 罗小杰. 也论覆盖型岩溶地面塌陷机理[J]. 工程地质学报, 2015, 23(5): 886-895. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201505011.htm [24] 罗小杰, 沈建. 我国岩溶地面塌陷研究进展与展望[J]. 中国岩溶, 2018, 37(1): 101-111. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR201801013.htm [25] 张杰, 毕攀, 魏爱华, 等. 基于模糊综合法的烟台市栖霞中桥岩溶塌陷易发性评价[J]. 中国岩溶, 2021, 40(2): 215-220. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR202102005.htm [26] HE K Q, JIA Y Y, CHEN W G, et al. Evaluation of Karst collapse risks induced by over-pumping and Karst groundwater resource protection in Zaozhuang region, China[J]. Environmental Earth Sciences, 2014, 71(8): 3443-3454.
[27] PERRIN J, CARTANNAZ C, NOURY G, et al. A multicriteria approach to Karst subsidence hazard mapping supported by weights-of-evidence analysis[J]. Engineering Geology, 2015, 197: 296-305.
[28] YAU K, PARASKEVOPOULOU C, KONSTANTIS S. Spatial variability of Karst and effect on tunnel lining and water inflow. A probabilistic approach[J]. Tunnelling and Underground Space Technology, 2020, 97: 103248.
[29] 朱庆杰, 刘挺权, 张秀彦. 唐山市岩溶塌陷的神经网络预测模型[J]. 辽宁工程技术大学学报, 2003, 22(6): 753-755. https://www.cnki.com.cn/Article/CJFDTOTAL-FXKY200306010.htm [30] 贺玉龙, 杨立中, 黄涛. 人工神经网络在岩溶塌陷预测中的应用研究[J]. 中国地质灾害与防治学报, 1999, 10(4): 86-90, 79. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH199904013.htm [31] 包惠明, 胡长顺. 岩溶地面塌陷神经网络预测[J]. 工程地质学报, 2002, 10(3): 299-304. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ200203015.htm [32] 陈静, 马亚杰, 朱庆杰. 人工神经网络模型在岩溶塌陷安全评价中的应用[J]. 地质灾害与环境保护, 2005, 16(2): 139-142, 146. https://www.cnki.com.cn/Article/CJFDTOTAL-DZHB200502006.htm [33] 谭文侃, 叶义成, 胡南燕, 等. LOF与改进SMOTE算法组合的强烈岩爆预测[J]. 岩石力学与工程学报, 2021, 40(6): 1186-1194. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106010.htm [34] 陈瑜. 离群点检测算法研究[D]. 兰州: 兰州大学, 2018. [35] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357.
[36] 崔鑫. 面向不均衡数据集的分类算法研究[D]. 无锡: 江南大学, 2021. [37] 杨彪. 矿山地下水害防治工程可视化及地表塌陷预测研究[D]. 长沙: 中南大学, 2011. [38] 周爱红, 牛鹏飞, 袁颖, 等. 基于PCA-PSO-SVM的凡口铅锌矿地区岩溶地表塌陷危险性预测[J]. 中国岩溶, 2020, 39(4): 622-628. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGYR202004018.htm [39] 赖永标, 乔春生. 基于支持向量机岩溶塌陷的智能预测模型[J]. 北京交通大学学报, 2008, 32(1): 36-39, 43. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT200801010.htm
下载:
计量
- 文章访问数: 95
- HTML全文浏览量: 13
- PDF下载量: 9
