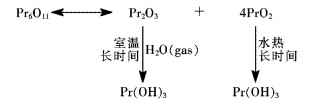
Storage stability of Pr6O11 at room temperature and analysis of its reactivity with water
-
摘要: 通过对实验室中自然储存10年的Pr6O11样品的分析,发现样品中含有质量分数约19 %的Pr(OH)3.采用热重(TG)、红外光谱(FTIR)和X射线衍射(XRD)对样品的组成进行分析.结果表明,样品中只有Pr6O11、PrO2和Pr(OH)3 3种物相.考察了纯Pr6O11在室温和相对湿度为100 %条件下样品质量随时间的变化,60 d后增重趋势减缓.用纯Pr6O11作为吸附剂对水溶液中磷酸根脱除实验进行了考察,验证了Pr6O11与H2O反应生成Pr(OH)3.通过在190 ℃下不同水热时间(24~96 h)观察,PrO2也可以与水缓慢反应生成Pr(OH)3.Abstract: The analysis for Pr6O11 stored for ten years in laboratory at ambient environment shows that the sample contains about 19 wt% Pr (OH)3. TG, FTIR and XRD analysis results show that there are three phases, namely Pr6O11, PrO2 and Pr (OH)3 in the sample. The mass change with the storage time was investigated in a closed ambient environment under the condition of 100 % relative humidity. The mass increasing tendency slows down after 60 d. Phosphate removal rate in aqueous solution was detected using pure Pr6O11 as adsorbent to find out that Pr6O11 reacts with H2O to generate Pr (OH)3. Pr6O11 can be completely converted into PrO2 and Pr (OH)3 under hydrothermal condition at 190 ℃. It is found that PrO2 can also react with water slowly to generate Pr (OH)3 at 190 ℃ for different hydrothermal time (24~96 h).
-
Keywords:
- praseodymium oxide /
- stability /
- hydrothermal reaction /
- praseodymium dioxide
-
氧化镨(Pr6O11)是轻稀土产品中的重要产品之一.因其具有独特的理化性质,故在陶瓷、玻璃、稀土永磁、催化剂、稀土抛光粉、研磨材料和添加剂等领域获得应用[1-7].通常人们认为稀土倍半氧化物可与空气中的水汽和CO2作用,特别是碱性较强的La2O3,更易发生这类作用,生成Ln(OH)3、LnOOH和碳酸盐或碱式碳酸盐[8-10].黄继民等[11]研究了La2O3在空气中的稳定性,发现在室温条件下La2O3粉末在空气中吸水增重,生成的产物为Ln(OH)3,没有发现有碳酸盐或碱式碳酸盐生成.Fleming等[12]也报道了暴露于水蒸汽中的La2O3粉末快速生成Ln(OH)3的反应.
在轻稀土氧化物中,镨的氧化物比较特殊,它的稳定氧化物为变价的Pr6O11,即氧化物中+3价和+4价的镨同时存在.轻稀土氧化物与空气中的水发生反应,这是一个不争的事实.但是Pr6O11与水反应速率如何?Pr6O11与空气中的CO2反应程度如何?这些问题还有待进一步研究.针对储存10 a的Pr6O11样品的研究发现有Pr(OH)3生成.因此,对Pr6O11在自然存放条件下的稳定性及其与水反应的活性的研究是十分必要的.
1 实验
1.1 实验原料
Pr6O11是2004年4月从江苏卓群纳米稀土股份有限公司采购的,纯度为99.95 %,储存10 a.Pr6O11原料储存在500 mL带有内衬盖的塑料瓶中,在实验室试剂柜中自然存放.夏季温度为20~30 ℃,相对湿度50 %~80 %,冬季温度为15~20 ℃,相对湿度为20 %~40 %.
1.2 实验方法
X射线衍射(XRD)测定采用D/max-RB衍射仪(日本理学),CuKα辐射,闪烁计数器前加石墨弯晶单色器,管流100 mA,管压40 kV,测角仪半径=185 mm,光阑系统为DS=SS=1 mm,RS=0.15 mm,样品填入深度为0.5 mm,采用θ~2θ连续扫描方式,扫描速度6°/min,步长0.02 mm;
热重分析(TGA)测试采用Pyris 1型热重分析仪(美国Perkin Elmer),程序升温速度20 °C/min,温度范围30~800 ℃,气氛为流速20 mL/min的干燥空气,升温程序:30~800 ℃,20 ℃/min.
FTIR测试使用美国Perkin-Elmer公司Spectrum GX型傅里叶变换红外光谱仪(溴化钾压片法测定,光谱分辨率4 cm-1,测量范围4 000~400 cm-1)
2 结果和讨论
2.1 室温储存10 a的Pr6O11原料分析
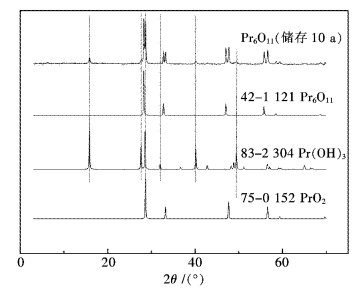
在轻稀土氧化物中,氧化镨与其它氧化物有明显区别,其显著的特点是镨的氧化态有+3和+4两种价态.图 1给出了储存10 a的Pr6O11的XRD谱图,从对比分析结果来看,样品中存在2种新物相:PrO2(JCPDS No.75-0152)和Pr(OH)3(JCPDS No.83-2304).从XRD分析结果可推断,Pr3+似乎更易于与水反应生成Pr(OH)3.
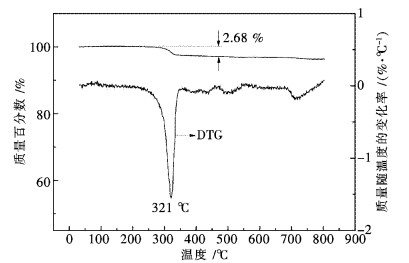
图 2给出了储存10 a的Pr6O11热重分析实验结果.从图 2 TG曲线可看出,在250 ℃之前没有失重,表明样品中不含游离水.在250~350 ℃范围内失重2.68 %,表明样品中的Pr(OH)3分解生成Pr6O11.从图 2 DTG曲线可看出,Pr(OH)3的最大失重速率对应的失水温度为321 ℃.与Ln(OH)3和Nd(OH)3热分解过程不同的是,Pr(OH)3热分解脱水过程没有经历LnO(OH)(Ln=La,Nd)中间步骤.上述TG-DTG分析结果与文献[13-15]报道的Pr(OH)3的脱水过程基本吻合.根据2.68 %失重率计算,储存10 a的Pr6O11样品中含Pr(OH)3的质量百分数为19.1 %,这充分说明Pr6O11在自然储存条件下与空气中的水反应速度是非常缓慢的.
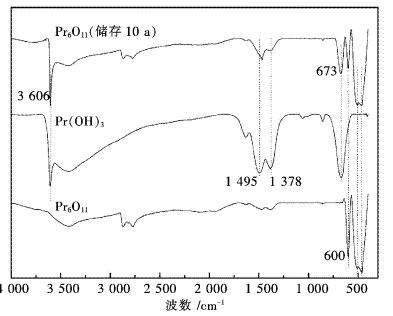
为进一步证实上述XRD和TG分析结果,采用FTIR技术对样品进行了分析,结果见图 3.从图 3可看出,样品在3 606 cm-1处有一个强而尖锐的特征峰,这是典型的Pr(OH)3中的-OH的伸缩振动峰,此外在指纹区673 cm-1处的特征峰与纯Pr(OH)3的峰非常吻合,表明样品中存在Pr(OH)3.此外,样品在指纹区400~600 cm-1处的3个峰与纯Pr6O11的特征峰也非常吻合,这表明样品中仍然存在大量的Pr6O11没有与水反应.从图 3中仍然没有观察到CO32-的特征峰,因为CO32-的特征峰有4个,分别为:1 463 cm-1(非对称收缩)、1 064 cm-1(对称收缩)、855 cm-1(面外弯曲)和746 cm-1(面内弯曲)[16-17].从图 3中没有检测到这些CO32-特征峰.
2.2 纯Pr6O11在潮湿空气中室温储存稳定性
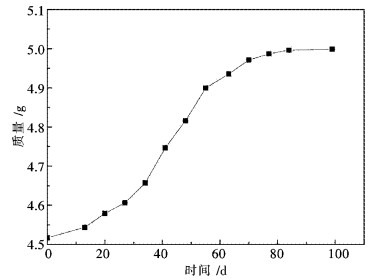
图 4给出了Pr6O11在相对湿度为100 %的密闭环境质量随时间变化曲线,从图 4中可看出x.在前60 d内,曲线斜率较大,说明Pr6O11与空气中的水反应速度较快,60 d以后,曲线斜率较小,反应速度相对较慢.这是因为先期生成的Pr(OH)3包覆了颗粒表面,一定程度上阻止了水汽与Pr6O11的接触.
2.3 纯Pr6O11的水热反应产物分析
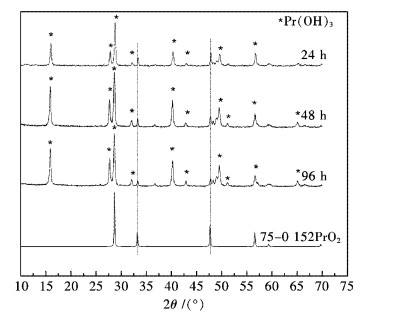
上述分析实验证明Pr6O11中的Pr2O3更容易与水反应,而PrO2与水似乎很难反应.为了证实这一点,将1.25 g Pr6O11和20 mL纯水置于40 mL聚四氟乙烯内衬水热合成反应釜中,在190 ℃分别反应24 h、48 h和96 h,产物XRD分析见图 5.从图 5可看出,随着水热反应时间的延长,PrO2始终存在于反应产物中,通过观察32.1°与33.4°峰高的比例可看出,随着反应时间延长,PrO2有逐渐减小的趋势,这说明PrO2在水热条件下是可以与纯水反应的,只不过反应速度极慢而已.
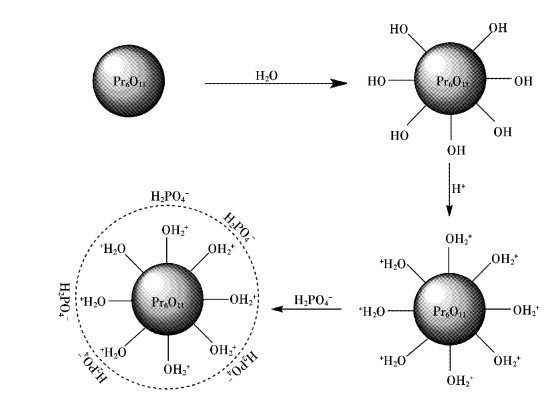
2.4 纯Pr6O11储存过程中与水反应的机理分析
在纯Pr6O11中,镨的氧化态有+3和+4两种价态,它可以被看作为Pr2O3和PrO2复合而成的.其中Pr2O3在室温下就可以与空气中的水汽反应生成Pr(OH)3.而PrO2在室温下很难与空气中的水汽反应,只有在水热条件下经过长时间的反应,才可以缓慢转变为Pr(OH)3.反应机理见图 6.
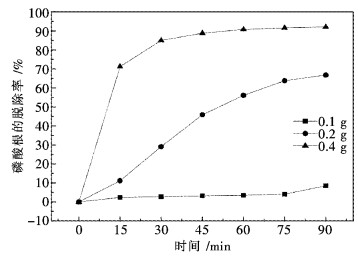
2.5 纯Pr6O11吸附水溶液中磷酸根
近年来,有文献报道Pr(OH)3对水溶液中的染料及磷酸根具有极强的吸附能力[18-20].文献[21]研究了La2O3对水溶液中磷酸根的吸附机理,发现La2O3首先与水反应生成Ln(OH)3,起吸附作用的是Ln(OH)3而非La2O3.为进一步验证Pr6O11与H2O反应生成Pr(OH)3,用纯Pr6O11作为吸附剂,对水溶液中磷酸根脱除实验进行了考察,吸附条件为:pH=2,磷酸根水溶液用量200 mL(浓度100 mg PO43-/L,用磷酸二氢钾配制),温度25 ℃.图 7为不同Pr6O11用量时的磷酸根脱除率随时间变化的曲线.磷酸根脱除率的定义如下:
$$ 磷酸根脱除率/{\rm{\% = }}\frac{{{C_{\rm{o}}} - {C_t}}}{{{C_{\rm{o}}}}}{\rm{ \times }}100{\rm{\% }} $$ Co表示初始磷酸根浓度,Ct表示t时刻(min)时水溶液中磷酸根浓度.
从图 7的吸附曲线可看出,当Pr6O11用量分别为0.1 g和0.2 g时,磷酸根的脱除率随时间的变化呈现近似于线性的关系.这表明Pr6O11逐渐与水反应生成Pr(OH)3,逐步生成的Pr(OH)3不断吸附水溶液中的磷酸根.当Pr6O11用量为0.4 g时,在15 min时磷酸根脱除率即可达到71.2 %,随后逐渐趋向于吸附平衡.当Pr6O11用量为0.1 g时,磷酸根脱除率很低,表明生成Pr(OH)3的量很少,不足于吸附水溶液中的磷酸根.
图 8给出了Pr6O11吸附水溶液中磷酸根的吸附机理.当Pr6O11颗粒与水接触时,在颗粒表面逐渐生成Pr(OH)3,从而使颗粒表面富含羟基,在弱酸性条件下,表面OH-被质子化,使得颗粒表面形成一个正电荷的氛围(图 8中虚线圆圈部分),与带有负电荷的H2PO4-发生静电吸引作用,从而实现对PO43-的吸附.
3 结论
1)Pr6O11在储存过程中与空气中的水发生缓慢化学反应生成Pr(OH)3.
2)经过长期自然存放的Pr6O11在使用前应在700~800 ℃焙烧,以保证准确的化学计量组成.
3)无论是在自然储存还是在高温水热条件下,Pr6O11中的三价Pr更容易与水反应,得到的产物为PrO2和Pr(OH)3的混合物.
4)Pr6O11可作为吸附水溶液中磷酸根的吸附剂,其机理在于原位生成的Pr(OH)3表面羟基形成静电吸引层.
-
-
[1] Li H, Wang S, Huang Z, et al.Thermal stability and electrochemical performance of Polyaniline/Pr6O11 composites[J].Polymers for Advanced Technologies, 2014, 25(1): 66-72. doi: 10.1002/pat.v25.1
[2] Masui T, Nagai R, Imanaka N.Effect of the introduction of oxide ion vacancies into cubic fluorite-type rare earth oxides on the NO decomposition catalysis[J].Journal of Solid State Chemistry, 2014, 220: 181-184. doi: 10.1016/j.jssc.2014.08.029
[3] Treu B L, Fahrenholtz W G, O'Keefe M J.Thermal decomposition behavior of praseodymium oxides, hydroxides, and carbonates[J].Inorganic Materials, 2011, 47(9): 974-978. doi: 10.1134/S0020168511090214
[4] Jeeva Jothi K, Palanivelu K.Facile fabrication of core-shell Pr6O11-ZnO modified silane coatings for anti-corrosion applications[J].Applied Surface Science, 2014, 288: 60-68. doi: 10.1016/j.apsusc.2013.09.112
[5] Bahaa M, Abu-Zied, Youssef A.Mohamed, Abdullah M.Asiri.Fabrication, characterization, and electrical conductivity properties of Pr6O11 nanoparticles[J].中国稀土学报:英文版, 2013, 31(7): 701-708.
[6] 吴洋, 吴伯麟.稀土Pr6O11及其氢氧化物对高铝瓷耐磨性能的影响[J].陶瓷, 2014(5): 13-16. http://www.cqvip.com/QK/93394X/201405/49587104.html [7] 王秀芳.Sb2O3掺杂对Pr6O11压敏电阻微结构和电学性能的影响[J].人工晶体学报, 2013, 42(6): 1041-1045. http://www.cnki.com.cn/Article/CJFDTotal-GNCL200912018.htm [8] 苏锵.稀土化学[M].郑州:河南科学技术出版社, 1993: 204-205. [9] 徐光宪.稀土上册[M].北京:冶金工业出版社, 2002: 55. [10] 刘光华.稀土材料学[M].北京:化学工业出版社, 2007: 46. [11] 黄继民, 沈雷军, 韩莉, 等.La2O3在空气中稳定性的研究[J].稀土, 2002, 23(3): 72-73. http://d.wanfangdata.com.cn/Periodical/xitu200203021 [12] Fleming P, Farrell R A, Holmes J D, et al.The rapid formation of La (OH)3 from La2O3 powders on exposure to water vapor[J].Journal of the American Ceramic Society, 2010, 93(4): 1187-1194. doi: 10.1111/jace.2010.93.issue-4
[13] Yan L, Yu R B, Liu G R, et al.A facile template-free synthesis of large-scale single crystalline Pr (OH)3 and Pr6O11 nanorods[J].Scripta Materialia, 2008, 58: 707-710. doi: 10.1016/j.scriptamat.2007.12.007
[14] Ma L, Chen W X, Zhao J, et al.Synthesis of Pr (OH)3 and Pr6O11 nanorods by microwave-assisted method: Effects of concentration of alkali and microwave heating time[J].Journal of Crystal Growth, 2007, 303: 590-596. doi: 10.1016/j.jcrysgro.2006.12.035
[15] Zhao J, Chen W X, Yu G Y, et al.Synthesis and characterization of praseodymium hydroxide nanorods by a hydrothermal process[J].Chemistry Letters, 2005, 34(5): 738-739. doi: 10.1246/cl.2005.738
[16] Nakamoto K.Infrared and Raman spectra of inorganic and coordination compounds[M].New York: John Wiley and Sons Inc, 1986: 252-255.
[17] 孙育斌.氧化镨标样中水化相的结构[J].分析测试学报, 1998, 17(6): 22-24. http://www.cnki.com.cn/Article/CJFDTOTAL-TEST806.005.htm [18] Zhai T, Xie S, Lu X H, et al.Porous Pr (OH)3 nanostructures as high-efficiency adsorbents for dye removal[J].Langmuir, 2012, 28(30): 11078-11085. doi: 10.1021/la3013156
[19] Tang J P, Chen J, Huang W Y, et al.Porous Pr (OH)3 nanowires as novel high-performance adsorbents for phosphate removal[J].Chemical Engineering Journal, 2014, 252: 202-209. doi: 10.1016/j.cej.2014.04.091
[20] Sun X F, Zhai T, Lu X H, et al.Facile synthesis of Pr (OH)3 nanostructures and their application in water treatment[J].Materials Research Bulletin, 2012, 47: 1783-1786. doi: 10.1016/j.materresbull.2012.03.024
[21] 陆岩, 刘艳磊, 姜恒, 等.氧化镧对磷酸根的吸附及其机理研究[J].化工科技, 2014(1): 45-48. http://www.cnki.com.cn/Article/CJFDTOTAL-JKGH201401011.htm



 下载:
下载: