风化壳淋积型稀土矿勘探网度优化的特征点法

邓祖建; 龙平; 洪本根; 黄豪; 王明照; 王观石; 钟贞明

doi:10.13264/j.cnki.ysjskx.2025.01.017

风化壳淋积型稀土矿勘探网度优化的特征点法

1.
江西理工大学土木与测绘工程学院,江西赣州341000
2.
厦门钨业股份有限公司,福建厦门364000
3.
江西应用技术职业学院,江西赣州341000

基金项目:

国家自然科学基金资助项目 52364015

江西省自然资源厅科技创新项目 ZRKJ20222402

详细信息

通讯作者:
龙平（1992—　）,博士,讲师,主要从事离子型稀土资源绿色提取等方面的研究工作。E-mail：longp1234@163.com

计量
- 文章访问数: 7
- HTML全文浏览量: 2
- PDF下载量: 2
出版历程
- 收稿日期: 2024-02-28
- 修回日期: 2024-03-24
- 刊出日期: 2025-02-27

Characteristic point method for optimizing exploration network of weathered crust elution-deposited rare earth ore

1.
School of Civil and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou341000, Jiangxi, China
2.
Xiamen Tungsten Industry Co., Ltd., Xiamen364000, Fujian, China
3.
Jiangxi College of Applied Technology, Ganzhou341000, Jiangxi, China

摘要

摘要:
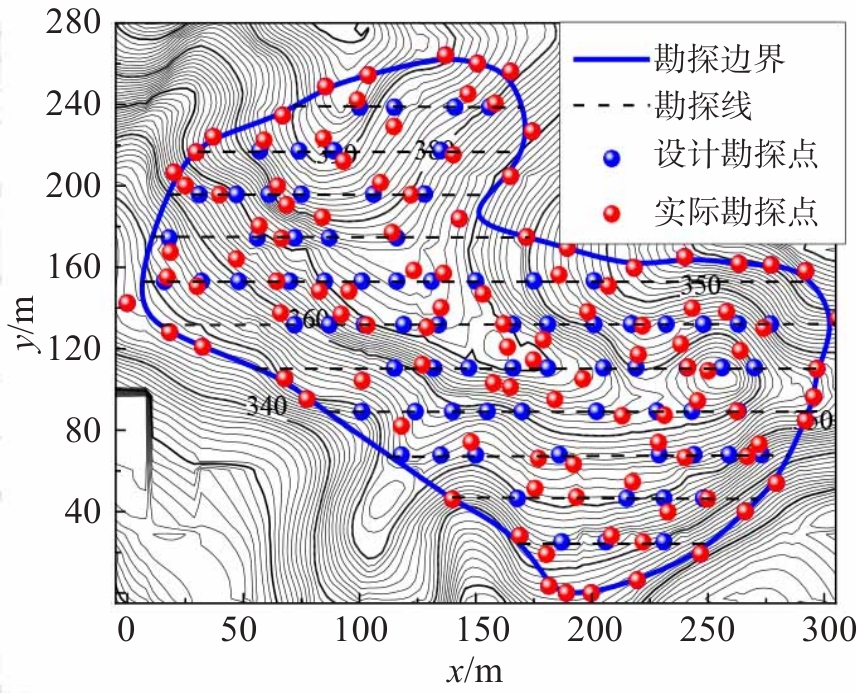
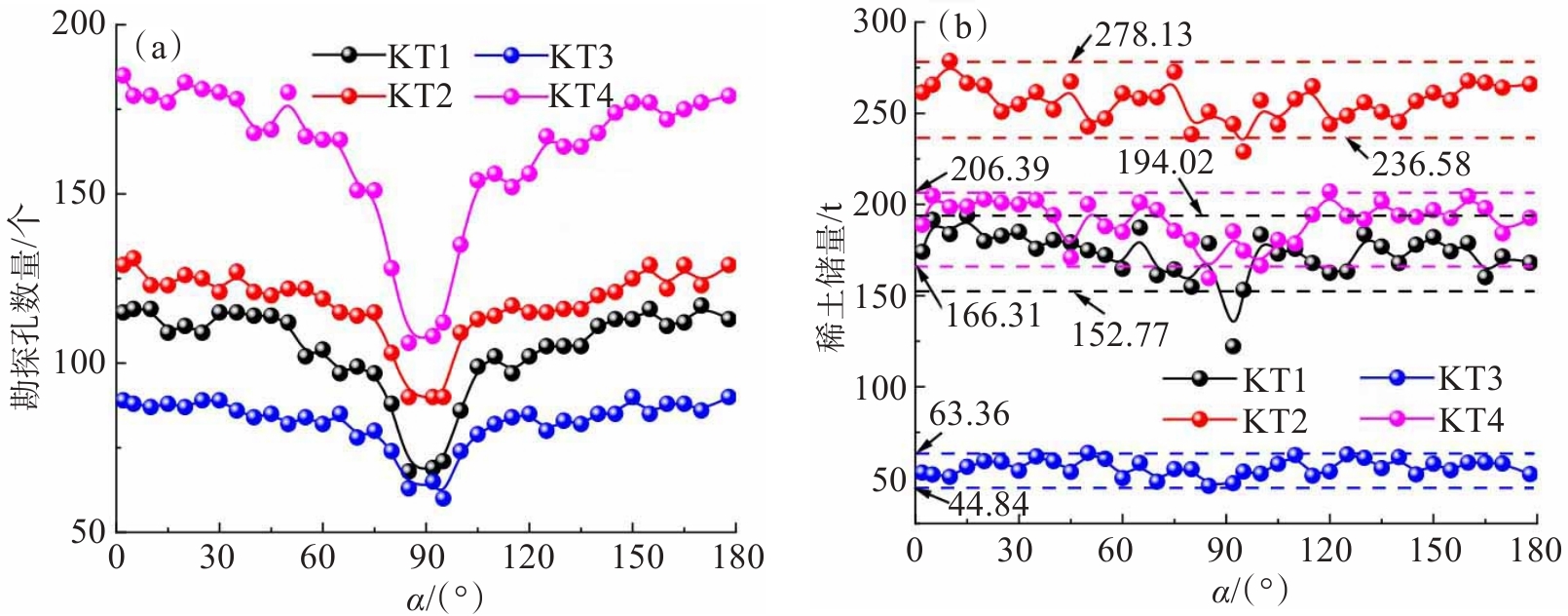
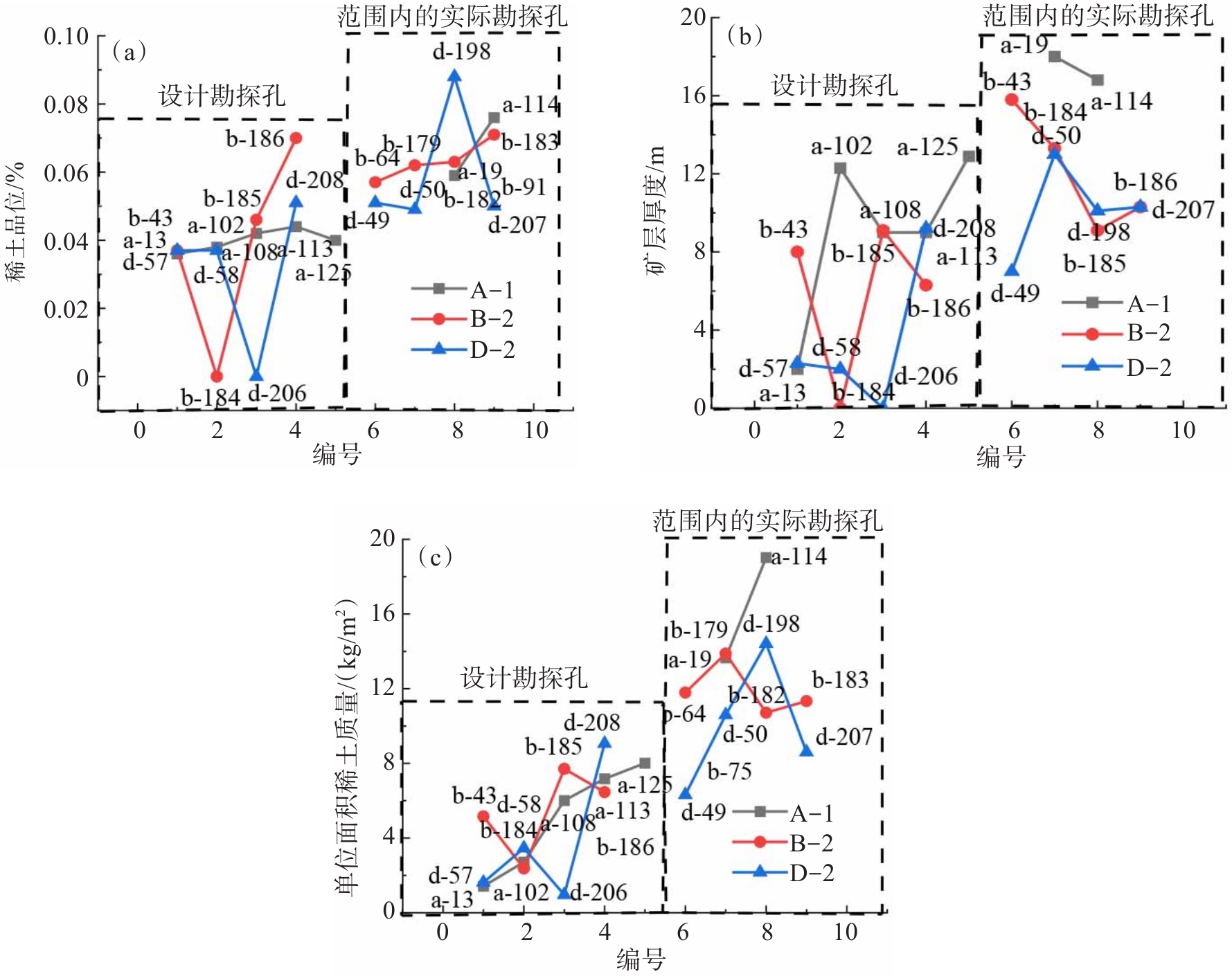
风化壳淋积型稀土矿稀土品位具有明显的空间变异性,均匀布置勘探孔容易出现品位变异性大的区域勘探孔不足和变异性小的区域勘探孔过多的问题。本文假设矿体的单位面积稀土质量分布与地形高程的变化剧烈程度存在正相关关系,以地形的特征点作为稀土储量勘探点,建立了风化壳淋积型稀土矿勘探网度优化的特征点法,通过实际矿体讨论该方法的合理性。结果表明,单位面积稀土质量与勘探孔孔口高程的平均曲率的相关系数大于0.390,说明基本假设是合理的。当勘探线与正东的方向夹角在90°附近时,勘探孔数量取得最小值。与实际勘探结果相比,特征点法可以减少20.00%的勘探孔数量,稀土储量的计算误差小于8.00%。研究成果可以为风化壳淋积型稀土矿的高效勘探提供技术支持。
- 风化壳淋积型稀土矿 /
- 勘探 /
- 特征点 /
- 垂距法
Abstract:
Weathered crust elution-deposited rare earth ore exhibits significant spatial variability in rare earth grades. Uniform placement of exploration holes is prone to the problem of insufficient exploration holes in areas of high-grade variability and too many exploration holes in areas of low variability. Assuming that there is a positive correlation between the distribution of rare earth mass per unit area in the ore body and the intensity of changes in terrain elevation, a characteristic point method for optimizing the exploration network of weathered crust elution-deposited rare earth ore was established by taking terrain features as exploration points for rare earth reserves. The rationality of the proposed method was varied through actual ore bodies. The correlation coefficient between the rare earth mass per unit area and the orifice elevation of exploration holes is higher than 0.390, indicating that the assumption was reasonable. The direction angle of the exploration line is around 90° to due east, where the number of exploration holes reaches a minimum. Compared to the actual exploration results, the characteristic point method can reduce the number of exploration holes by 20.00%, and the calculation error in rare earth reserves is less than 8.00%. The research provides theoretical support for the efficient prospecting for weathered crust elution-deposited rare earth ore.
- weathered crust elution-deposited rare earth ore /
- prospecting /
- characteristic point /
- vertical distance method
王庆龙

HTML全文

多台阶高陡岩质边坡的稳定性问题一直是地质工程领域的研究热点之一^[1]。这类边坡常见于矿山开采、道路建设以及水库工程中,因其特殊的地质条件和施工环境,极易受到爆破与自然风化的影响,而导致其发生变形破坏^[2]。爆破作为岩体掘进过程中不可或缺的技术手段,虽然可以有效地促进工程进度,但也不可避免地对边坡岩体结构产生扰动,使得岩体内原有的力学平衡被打破^[3]。与此同时,自然风化过程长期作用于岩质边坡表面,导致岩石物理力学性能逐渐劣化,从而加剧了边坡的不稳定性^[4-6]。在爆破与自然风化的共同作用下,边坡变形发展成为一个复杂的动态过程,进而诱发一系列地质灾害,如滑坡、崩塌和泥石流等,不仅威胁着工程安全,还对周边环境和人类活动造成了严重的威胁^[7]。例如,1963年意大利北部瓦伊昂水库附近的山体发生大规模滑坡,造成了约2 000人死亡^[8]；2008年汶川地震引发了一系列山体滑坡与崩塌,这些次生灾害进一步加剧了灾情的严重性^[9]。

通过高精度地对边坡变形趋势的预测,可以为边坡工程的安全设计和灾害预警提供科学依据,从而有效地预防地质灾害的发生,保障人员及工程的安全^[8-12]。目前,常用的传统变形预测方法包括物理模型实验、数值模拟和统计分析等^[13-17]。这些方法虽然在一定程度上能够反映边坡变形的趋势,但也存在着显著的不足^[18-20]。物理模型实验受限于实验条件,难以全面反映实际边坡的复杂性；数值模拟方法则依赖于边坡模型参数的准确性,而这些参数往往难以通过现场测试精确获取；统计分析方法在处理非线性和时变特性明显的边坡变形数据时,预测精度较低,难以满足实际工程的需求。

为克服传统方法的不足,深度学习在处理时间序列问题能力备受关注,其中主要包括GRU、LSTM、Bi-LSTM、BERT和Transformer等模型。相较于LSTM模型,GRU模型具有更少的参数,但其在处理复杂长序列数据时,效果通常不如LSTM和Bi-LSTM模型,在边坡变形预测过程中,下一时刻位移变形不仅依赖于历史数据,还会受到天气、爆破等因素的干扰,而LSTM模型只能捕捉到前向依赖关系,无法充分利用时间序列中的所有信息。BERT模型复杂且资源消耗较大,训练与推理成本较高,更擅于长文本分类、系统问答等任务,对时间序列预测任务处理能力一般。Transformer模型在处理大规模数据与高并发任务时表现出色,但对于边坡变形预测这种数据量相对较少的任务,发挥不了其优势,且其对计算资源需求巨大。相较于其他的时间序列建模方法,Bi-LSTM-SA（Bidirectional Long Short-Term Memory Self-Attention）融合模型结合了双向长短期记忆网络（Bi-LSTM）与自注意力机制（SA）的优势,能够有效地捕捉边坡变形数据中的时序特征和全局依赖关系。双向长短期记忆网络则通过前向和后向2个方向的信息传播,提高了模型对边坡变形数据的预测精度,自注意力机制通过计算输入序列中各元素之间的相关性,增强了模型对重要特征的识别能力。因此,Bi-LSTM-SA融合模型在处理非线性、时变性强、时序关联性及高维性的边坡变形数据方面具有显著的优势,能够提供更加精准和可靠的变形预测结果,该模型已被广泛地应用在故障诊断^[21]、仪器设备剩余寿命预测^[22]及时间序列预测^[23]等领域。

综上所述,本研究旨在通过Bi-LSTM-SA融合模型的应用,提高多台阶高陡岩质边坡变形预测的精度和可靠性,为边坡工程的安全设计和地质灾害预警提供技术支持,具有重要的理论意义和实际价值。

1 算法模型的基本原理及评价方法

1.1 双向长短期记忆网络

LSTM模型通过引入门控机制解决了标准RNN模型在处理长序列时梯度消失和梯度爆炸的问题。LSTM模型的基本结构包括输入门、遗忘门、输出门以及一个细胞状态^[24]。

1）输入门：其功能可以分2个部分。一部分是判断当前输入信息的重要程度,确定需要更新的细胞状态,另一部分是把需要更新的信息传入细胞状态,完成对细胞状态的更新。

输入门在t时刻的输出结果如式（1）所示：

i_{t} = σ (W_{i} \cdot [h_{t - 1}, x_{t}] + b_{i})

(1)

新的候选细胞状态如式（2）所示：

{\tilde{C}}_{t} = t a n h (W_{C} \cdot [h_{t - 1}, x_{t}] + b_{C})

(2)

式（1）、式（2）中： $σ$ 表示激活函数； $W_{i}$ 与 $W_{C}$ 分别表示输入门确定细胞状态的权重系数与更新细胞状态的权重系数； $b_{i}$ 与 $b_{C}$ 分别表示输入门确定细胞状态的偏置项与更新细胞状态的偏置项； $t a n h$ 表示激活函数。输入门根据当前输入信息 $x_{t}$ 与上一时刻的隐藏层状态 $h_{t - 1}$ 。

2）遗忘门：其功能是根据输入门的输出结果,判断模型中细胞状态所要丢弃与保留的信息。遗忘门的计算方程如式（3）所示：

f_{t} = σ (W_{f} \cdot [h_{t - 1}, x_{t}] + b_{f})

(3)

式（3）中： $x_{t}$ 表示t时刻的输入数据； $f_{t}$ 表示遗忘门的计算结果； $h_{t - 1}$ 表示隐藏层状态； $σ$ 表示遗忘门的激活函数； $W_{f}$ 表示遗忘门的权重系数； $b_{f}$ 表示遗忘门的偏置项。

3）细胞状态：结合输入门的输出结果与遗忘门计算结果,对细胞状态进行更新,而细胞状态就是LSTM神经网络保留长期记忆的地方。细胞状态更新过程如式（4）所示：

C_{t} = f_{t} \times C_{t - 1} + i_{t} \times {\tilde{C}}_{t}

(4)

式（4）中： $f_{t}$ 表示遗忘门在t时刻的输出结果； $C_{t - 1}$ 表示细胞状态在t-1时刻的长时记忆输入； ${\tilde{C}}_{t}$ 表示细胞状态在t-1时刻的候选值； $i_{t}$ 表示输入门在t时刻的输出结果。

4）输出门：根据细胞状态更新结果计算对隐藏层状态的影响,并结合输出门的输出结果与细胞状态信息更新隐藏层状态。输出门计算公式如式（5）、式（6）所示：

o_{t} = σ (W_{o} [h_{t - 1}, x_{t}] + b_{o})

(5)

h_{t} = o_{t} * t a n h (C_{t})

(6)

式（5）、式（6）中： $o_{t}$ 表示输出门在时刻t的输出结果； $h_{t}$ 表示短时记忆的输出结果。

Bi-LSTM是一种改进的RNN,Bi-LSTM网络模型是通过同时训练2个LSTM网络,包含一个正向LSTM网络（从前到后处理序列的能力）和一个反向LSTM网络（从后到前处理序列的能力）,通过在正向和反向2个方向上处理序列数据,进而实现对时间序列数据中前后信息的依赖关系捕捉,如图1所示。每个时间步的输出都由正向LSTM与反向LSTM的隐藏状态拼接而成。现假设输入序列为 ${x_{1}, x_{2}, \dots, x_{t}}$ ,则Bi-LSTM计算过程如下。

图 1 Bi-LSTM算法流程

Figure 1. Flowchart of Bi-LSTM algorithm

下载: 全尺寸图片幻灯片

1）正向LSTM计算： $h_{t} = L S T M (x_{t}, h_{t - 1}, C_{t - 1})$ ；

2）反向LSTM计算： $h_{t} = L S T M (x_{t}, h_{t + 1}, C_{t + 1})$ ；

3）合并输出：将正向LSTM和反向LSTM的输出进行拼接或加权平均,得到时间序列数据的综合表示。

1.2 自注意力机制

SA（Self-Attention）网络是一种常被用于序列数据的处理,它通过计算输入序列中每个元素与其他所有元素之间的相关性,从而捕捉序列数据中的全局依赖关系。SA网络的优势在于,它能够并行处理序列数据,克服了传统RNN在处理长序列时的计算效率低下问题,同时,SA网络还能够有效地关注序列中的重要信息,提升模型的预测精度。SA网络主要包括以下几个步骤：

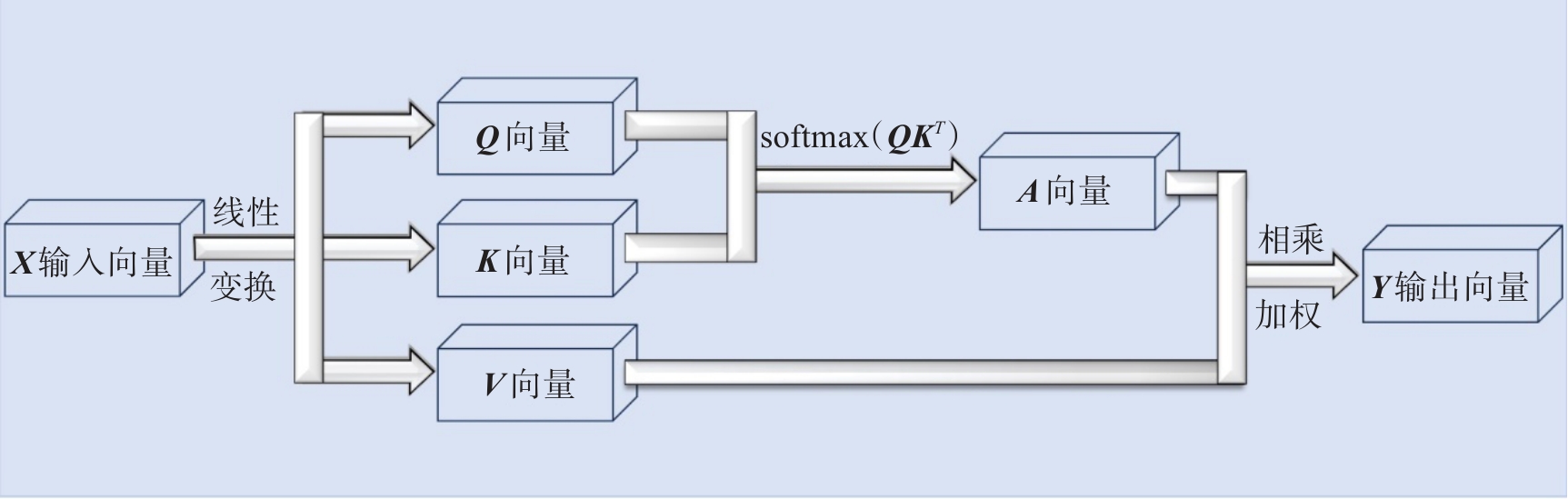
1）Query, Key, Value 体系：自注意力机制主要通过查询（Query）、键（Key）和值（Value）3个向量来运作,对输入序列中的每个元素进行不同的线性变换,产生一个Query向量、一个Key向量和一个Value向量,如图2所示。

图 2 自注意力机制算法流程

Figure 2. Flow chart of self-attention mechanism algorithm

下载: 全尺寸图片幻灯片

2）注意力分数计算：对于输入序列数据中第i个元素,它与输入序列数据中第j个元素之间的注意力分数 $s c o r e_{i j}$ ,可以通过Q向量与K向量通过计算得到,计算公式如式（7）所示：

s c o r e_{i j} = \frac{Q_{i} \cdot K_{j}^{T}}{\sqrt[]{d_{k}}}

(7)

式（7）中： $d_{k}$ 表示K向量的维度；缩放因子 $d_{k}$ 对于稳定softmax函数的梯度具有重要意义。

3）计算权重分配：将注意力分数计算结果通过softmax函数转换为概率分布数据,并将其作为各个元素的注意权重 $a_{i j}$ ,计算过程如式（8）所示：

a_{i j} = s o f t m a x (s c o r e_{i j})

(8)

4）加权求和：利用注意力权重对输入序列进行加权求和,得到序列的注意力表示,计算过程如式（9）所示：

C o n t e x t_{i} = \sum_{j = 1}^{n} a_{i j} V_{j}

(9)

式（9）中： $C o n t e x t_{i}$ 表示第i元素的注意力。

1.3 Bi-LSTM与SA融合模型

Bi-LSTM-SA模型结合了Bi-LSTM网络与SA网络的优势,用于预测多台阶高陡岩质边坡的变形。该模型通过Bi-LSTM捕捉序列中的前后文信息,并通过SA捕捉全局依赖关系,从而实现对多台阶高陡边坡变形的高精度预测。

Bi-LSTM与SA融合模型架构如下：

数据预处理：将日降雨量 $R = [r_{1}, r_{2}, \dots, r_{T}]$ 、蒸发量 $E = [e_{1}, e_{2}, \dots, e_{T}]$ 、炸药用量 $N = [n_{1}, n_{2}, \dots, n_{T}]$ 、监测点与爆破点之间距离 $L = [l_{1}, l_{2}, \dots, l_{T}]$ 进行归一化处理（T表示时刻）,并将其划分为训练集和验证集,输入特征向量为 $X_{t} = [R_{t}, E_{t}, N_{t}, L_{t}, c_{t}]$ , $c_{t}$ 表示t时刻累计位移量,训练集数据为 $[X_{t}, c_{t + 1}]$ 。

Bi-LSTM层：通过双向LSTM单元,分别在正向和反向上处理嵌入向量,得到正向和反向的LSTM输出。正向LSTM计算如下：

{\vec{h}}_{t} = L S T M (x_{t}, {\vec{h}}_{t - 1}, {\vec{C}}_{t - 1})

(10)

反向LSTM计算如下：

{\overset{⃖}{h}}_{t} = L S T M (x_{t}, {\overset{⃖}{h}}_{t + 1}, {\overset{⃖}{C}}_{t + 1})

(11)

Bi-LSTM输出为正向与反向输出的拼接：

h_{t} = [{\vec{h}}_{t}; {\overset{⃖}{h}}_{t}]

(12)

SA层：利用自注意力机制计算Bi-LSTM输出结果中的注意力权重,增强模型对重要时间步的关注,计算注意力权重并对隐藏状态进行加权。

计算加权隐藏层状态：

s_{t} = \sum_{t = 1}^{T} α_{t} h_{t}

(13)

式（13）中： $α_{t}$ 表示注意力权重系数。

融合层：将Bi-LSTM输出的隐藏状态与Self-Attention机制输出的加权隐藏状态进行融合,最终的融合特征如式（14）：

z_{t} = h {}_{t}\otimes s_{t}

(14)

输出层：通过全连接层将融合后的特征表示映射到目标输出 $c_{t + 1}$ ,即下一时刻的累计位移量。

c_{t + 1} = σ (W z_{t} + b)

(15)

式（15）中： $σ$ 表示激活函数；W表示全连接层的权重系数；b表示全连接层的偏置。

根据日降雨量、日蒸发量、炸药用量与监测点与爆破点之间距离等环境因素对边坡变形的影响,以及边坡变形监测数据构成时间序列,利用Bi-LSTM-SA融合模型提取输入时间序列之间的相互依赖关系,实现对多台阶高陡岩质边坡变形的预测。

1.4 模型评价指标

为了评价基于Bi-LSTM-SA融合模型的多台阶高陡边坡变形预测,本文选用方根误差（RMSE）、平均绝对误差（MAE）及决定系数（R²）3个指标对模型进行评价。其中,RMSE、MAE与R²的计算公式如式（16）、式（17）、式（18）所示：

R M S E = \sqrt[]{\frac{1}{m} \sum_{i = 1}^{m} (f (x_{i}) - y_{i})^{2}}

(16)

M A E = |\frac{1}{m} \sum_{i = 1}^{m} (f (x_{i}) - y_{i})|

(17)

R^{2} = 1 - \frac{\sum_{i = 1}^{m} (f (x_{i}) - y_{i})^{2}}{\sum_{i = 1}^{m} (\bar{y} - y_{i})^{2}}

(18)

式（16）—式（18）中：m表示数据集样本总数； $f (x_{i})$ 表示Bi-LSTM-SA融合模型的预测数据； $y_{i}$ 表示多台阶高陡边坡变形测量数据； $\bar{y}$ 表示多台阶高陡边坡变形测量数据的均值。决定系数用于评价模型预测数据与实测数据的相关性,其取值范围分布在0到1区间内,R²数值越大,表明Bi-LSTM-SA融合模型的预测效果越好。

2 工程案例分析

2.1 工程概况

本文以我国华东地区某露天矿山多台阶高陡岩质边坡为研究对象,台阶高度约为15 m,边坡角度约为70°,边坡由多个台阶组成,每个台阶的高度与边坡角度略有不同,边坡形貌如图3所示。多台阶高陡岩质边坡具有复杂的地质与几何特征,其稳定性受到降雨量、蒸发量及爆破扰动等多种因素的影响,通过合理地监测,可以有效地预防边坡失稳,保障露天矿山安全高效地开采。项目采用全站仪和GNSS技术相结合的方法,利用高精度全站仪对表面设定的监测点进行周期性观测,结合GNSS观测数据及全站仪测量数据,获取监测点的高精度三维坐标。

该边坡主要由软弱与半坚硬岩石组成,风化程度相对较高,呈破碎状结构,局部呈散体结构,整体强度相对较低,工程性能相对较差,在自然环境与爆破振动扰动共同作用下易发生滑坡等地质灾害,如图4所示。在边坡的关键位置（如台阶顶、台阶底、坡面中部）布设监测点,确保监测点布设均匀,覆盖整个监测区域,并且选择稳定的基准点作为参照点,基准点应远离监测区域。对露天采场北区、东区及南区建立了GNSS与全站仪监测点,监测网布设监测点40个,并建立2个基站和1个CORS站,建立了一套集监测数据自动化采集、传输及可视化呈现为一体的变形监测系统。

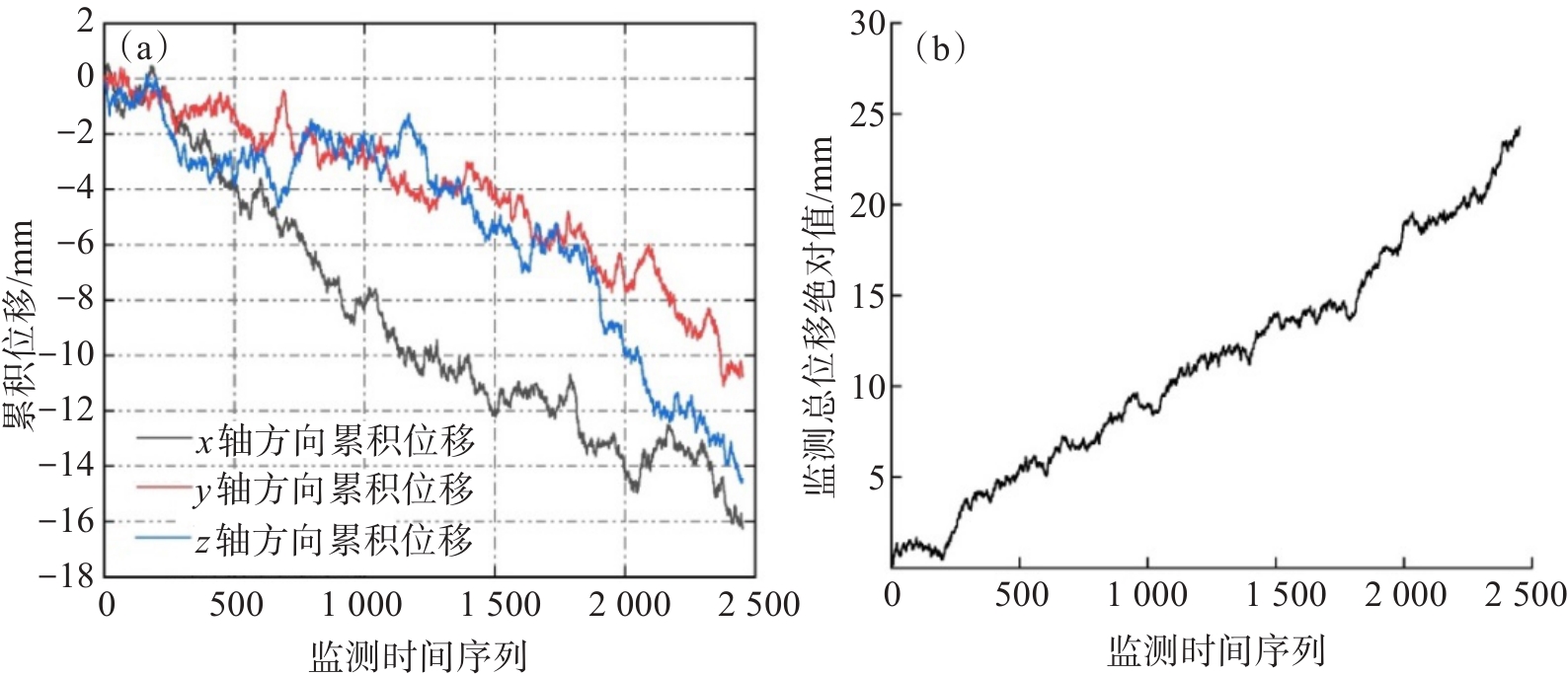
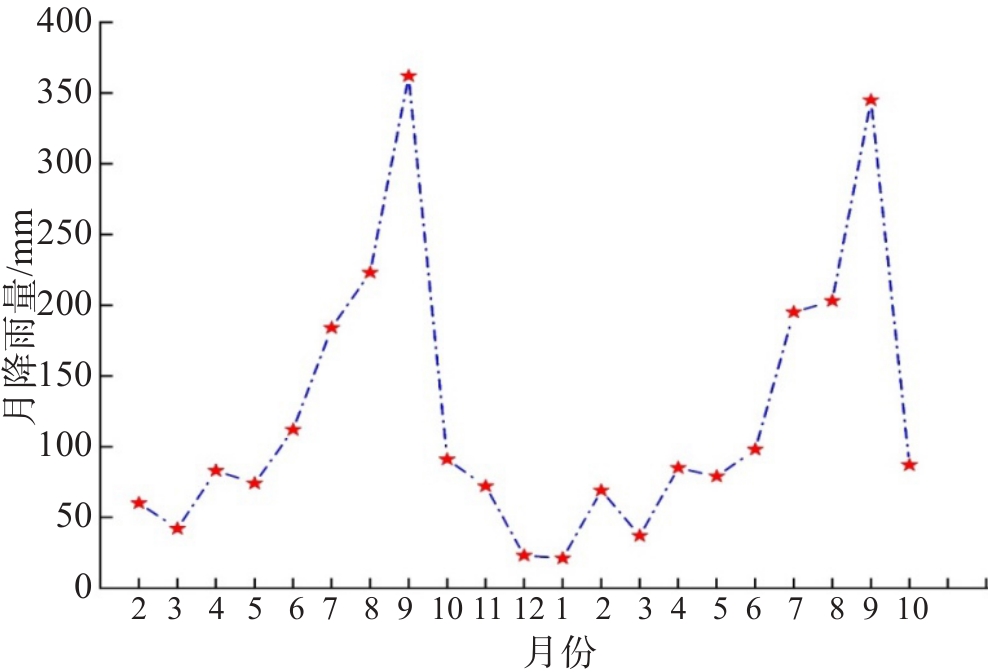
通常情况下各GNS与全站仪监测点每6 h测量一次,但在极端天气条件下GNS与全站仪监测点可以实现每5 min测量一次。利用Bi-LSTM-SA模型对所有监测点变形数据进行分析,发现各监测点的预测准确率较为接近,限于篇幅原因,本文随机选择了一个监测点数据进行了展示,设置每6 h对边坡数据进行采集一次,以2021年2月26日至2022年10月4日期间的监测数据为研究对象,共获得了2 452组监测数据,对上述数据进行预测分析。现以正北方向规定为x轴,正东方向规定为y轴,竖直方向规定为z轴方向,每个方向的累积监测位移如图5所示。监测区域2021年2月至2022年10月的降雨量统计结果如图6所示,降雨主要集中在每年的6—9月期间,最大月降雨量为362 mm。

图 5 监测点位移监测数据：（a）各方向监测数据；（b）监测总位移量数据

Figure 5. Displacement monitoring data of monitoring points：（a） monitoring data in all directions；（b） monitoring of total displacement data

下载: 全尺寸图片幻灯片

图 6 监测期间月降雨量统计

Figure 6. Monthly rainfall statistics during the monitoring period

下载: 全尺寸图片幻灯片

2.2 Bi-LSTM-SA融合模型的应用

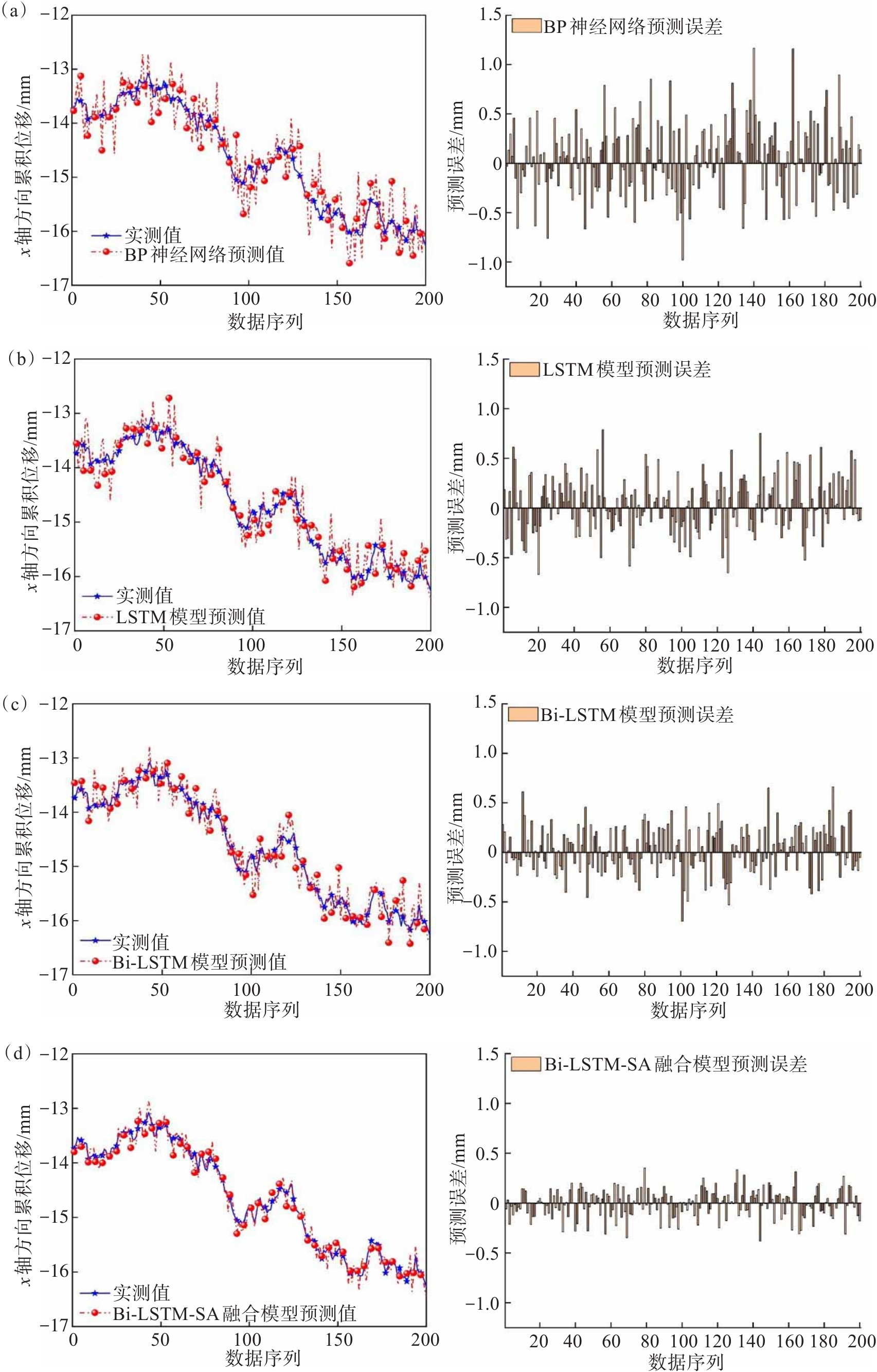
对监测数据进行预处理,将预处理后数据的前2 252组数据作为训练集,后200组数据作为测试集。利用Bi-LSTM-SA融合模型对训练集数据进行训练,使用均方误差作为损失函数,使用Adam优化器对Bi-LSTM-SA融合模型进行优化。为了验证Bi-LSTM-SA融合模型对台阶高陡边坡变形预测的准确性,将Bi-LSTM-SA融合模型的预测结果与BP神经网络、LSTN模型、Bi-LSTM模型的预测结果进行对比分析,同时将上述模型的预测结果与实测数据进行验证,验证本文提出Bi-LSTM-SA融合模型的可行性。

由图7可知：在相同输入参数条件下,相较于BP神经网络、LSTM模型与Bi-LSTM模型预测结果,Bi-LSTM-SA融合模型对多台阶高边坡在正南方的变形预测结果整体预测误差更小,同时Bi-LSTM-SA融合模型的预测结果与实测结果更为接近,验证了Bi-LSTM-SA融合模型在多台阶高陡边坡变形预测中的可行性。

图 7 x轴方向不同模型预测结果：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure 7. Prediction results of different models in x-axis direction: (a) BP neural network; (b) LSTM model ; (c) Bi-LSTM model; (d) Bi-LSTM-SA fusion model

下载: 全尺寸图片幻灯片

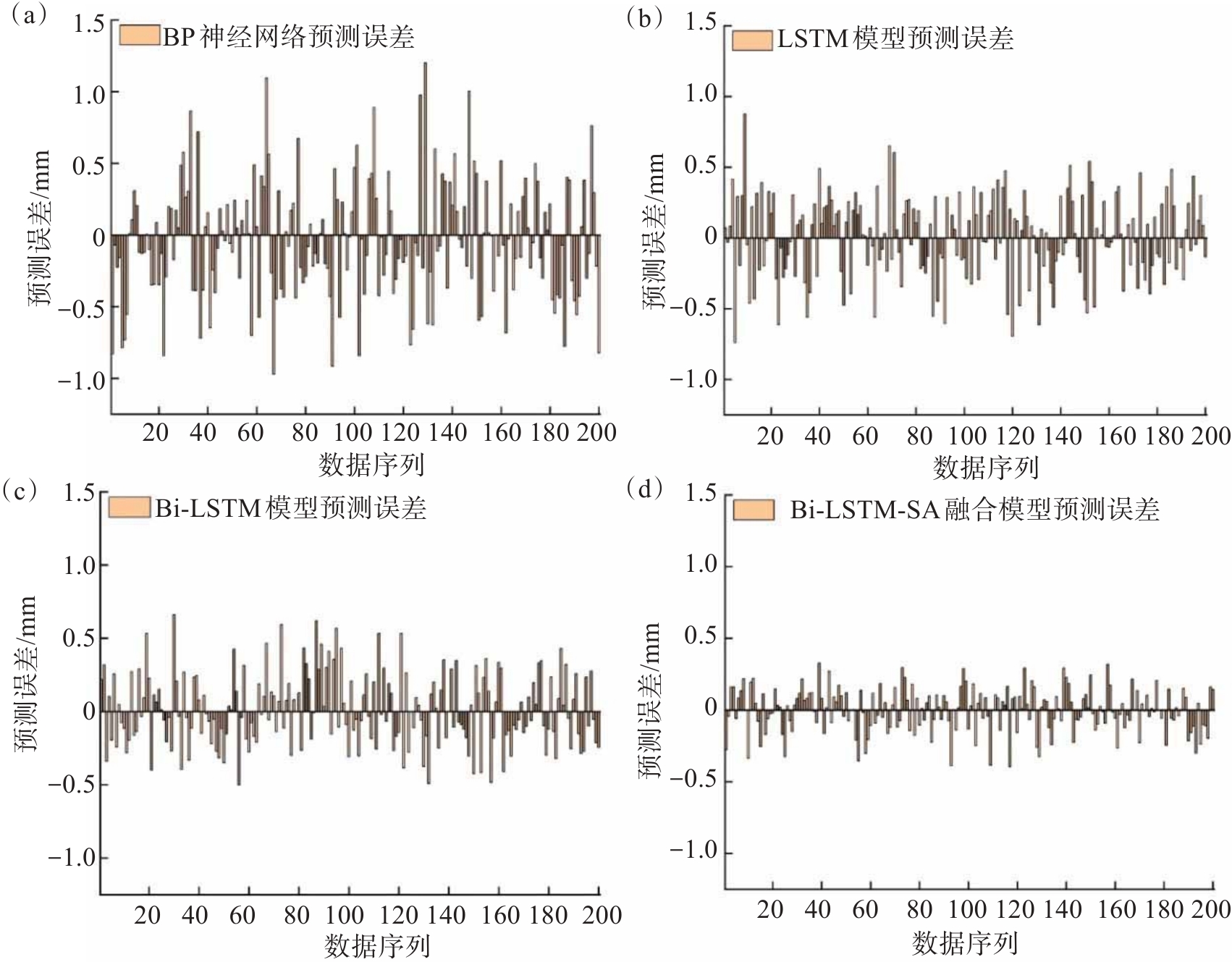
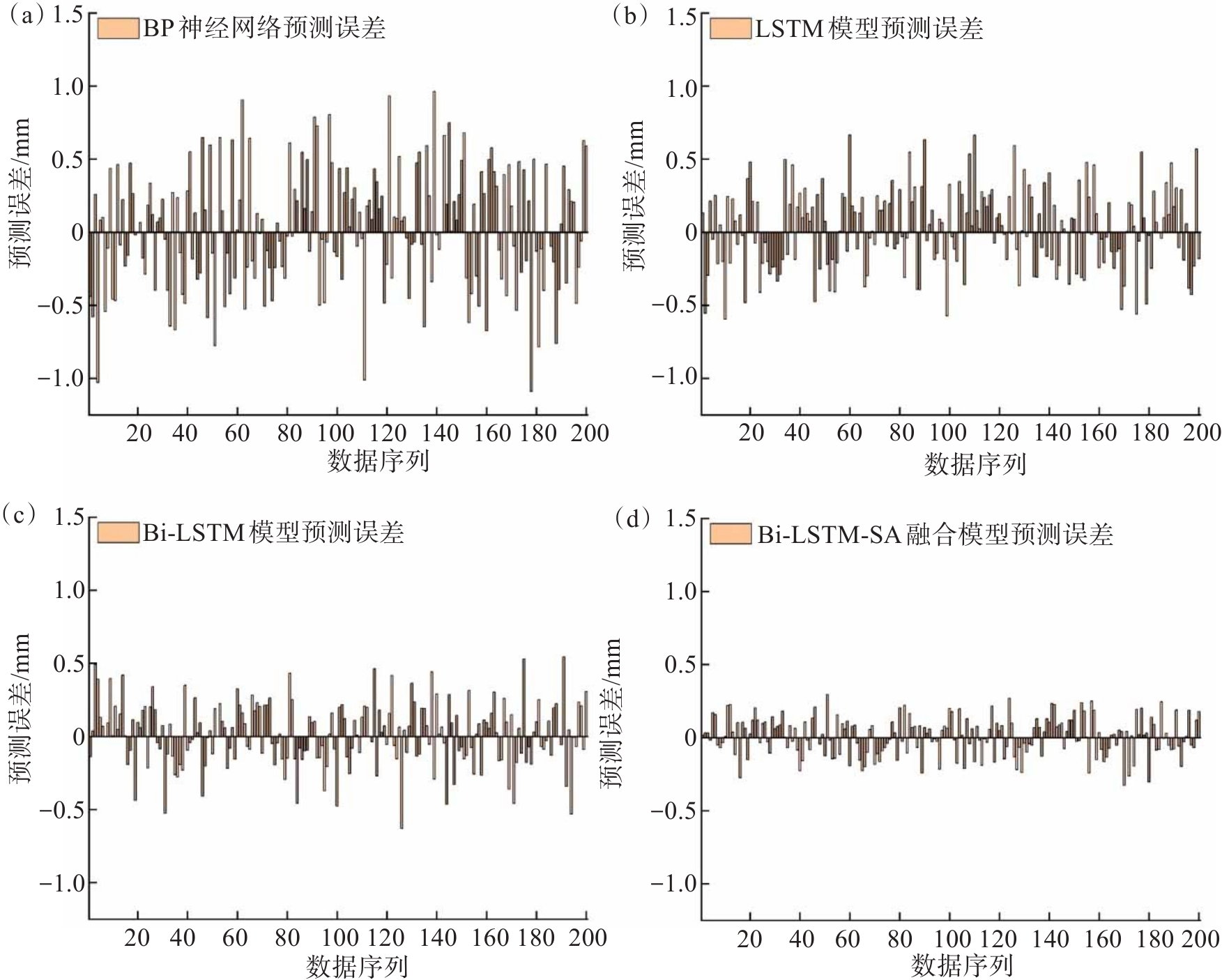
为了进一步验证Bi-LSTM-SA融合模型对多台阶高陡边坡变形预测的有效性,并提高预测效果的可靠性,本文对测试集数据的y轴与z轴方向预测误差进行了统计分析,如图8与图9所示。并对测试集的RMSE、MAE及R²进行了统计分析,如表1—表3所列,进而实现对不同模型预测性能进行分析。

图 8 y轴方向不同模型预测误差：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure 8. Prediction errors of models with different y-axis directions：（a） BP neural network；（b） LSTM model；（c） Bi-LSTM model；（d） Bi-LSTM-SA model

下载: 全尺寸图片幻灯片

图 9 z轴方向不同模型预测误差：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure 9. Prediction errors of models with different z-axis directions：（a） BP neural network ；（b） LSTM model；（c） Bi-LSTM model；（d） Bi-LSTM-SA model

下载: 全尺寸图片幻灯片

表 1 不同模型在x轴方向变形预测性能评价

Table 1. Evaluation of deformation prediction performance of different models in x-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.377 7	0.297 5	0.250 0	0.148 4
MAE	0.300 5	0.242 8	0.206 4	0.120 5
R²	0.836 8	0.895 0	0.912 9	0.959 4

下载: 导出CSV

| 显示表格

表 2 不同模型在y轴方向变形预测性能评价

Table 2. Evaluation of deformation prediction performance of different models in y-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.420 1	0.291 5	0.263 1	0.167 5
MAE	0.327 8	0.235 2	0.214 1	0.137 8
R²	0.810 4	0.908 7	0.915 7	0.959 9

下载: 导出CSV

| 显示表格

表 3 不同模型在z轴方向变形预测性能评价

Table 3. Evaluation of deformation prediction performance of different models in z-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.391 2	0.325 7	0.254 2	0.168 2
MAE	0.317 9	0.261 4	0.202 7	0.135 4
R²	0.835 6	0.886 0	0.916 4	0.946 9

下载: 导出CSV

| 显示表格

由图8、图9及表1—表3对比分析可知：BP神经网络的预测误差在-1~1.5 mm,最大值为1.42 mm, 3个方向预测结果的误差RMSE最大值为0.420 1,MAE最大值为0.327 8,R²最小值为0.810 4；LSTM模型的预测误差在-1~1 mm,最大值为0.95 mm,3个方向预测结果的误差RMSE最大值为0.325 7,MAE最大值为0.261 4,R²最小值为0.886 0；Bi-LSTM模型的预测误差在-0.75~0.75 mm,最大值为0.72 mm,3个方向预测结果的误差RMSE最大值为0.263 1,MAE最大值为0.214 1,R²最小值为0.912 9；Bi-LSTM-SA融合模型的预测误差在-0.5~0.5 mm,最大值为0.38 mm,3个方向预测结果的误差RMSE最大值为0.168 2,MAE最大值为0.137 8,R²最小值为0.946 9。实验结果表明,Bi-LSTM-SA融合模型预测结果能够与实测结果较好地拟合,较为准确地预测多台阶高陡边坡监测点3个方向的位移变化情况。

上述实验结果对比分析也表明了Bi-LSTM-SA融合模型不仅有较强的预测性能,也具有较好的可行性。

3 结论

本文采用不同预测模型对多台阶高陡边坡监测点3个方向的位移变化进行了分析,并通过方根误差、平均绝对误差及决定系数3个指标对预测模型性能进行了评价,以我国华东地区某一多台阶高陡边坡监测数据为研究对象,对监测点3个方向的累积位移进行了预测,得到了以下结论：

1）在相同的输入条件下,相较于BP神经网络、LSTM模型与Bi-LSTM模型预测结果,Bi-LSTM-SA融合模型对多台阶高边坡在3个监测方向的变形预测结果整体预测误差更小,同时Bi-LSTM-SA融合模型的预测结果与实测结果更为接近。

2）将日降雨量、日蒸发量、炸药用量及监测点与爆破点之间的距离及日位移量等因素影响作为输入数据,考虑了自然风化与爆破扰动共同作用下多台阶高陡边坡变形特点,构建的Bi-LSTM-SA融合预测模型。Bi-LSTM-SA融合模型预测性能更强,而且还表现出了更好的稳定性与鲁棒性。

3）为了更为有效地指导露天矿山边坡的安全管理,后期应当更加充分地利用监测数据与Bi-LSTM-SA融合模型,实现对复杂环境条件下多台阶高陡边坡变形的有效预测,为边坡滑坡等地质灾害的预警工作提供技术支持。

王庆龙

图 1 开采矿体地形及边界

Fig 1. Topography and boundary of the ore body to be mined

下载: 全尺寸图片幻灯片

图 2 根据地形筛选勘探孔孔口坐标的流程示意

Fig 2. Flowchart for screening the coordinates of exploration hole openings based on topography

下载: 全尺寸图片幻灯片

图 3 矿体地形、勘探边界以及勘探孔的位置：（a） KT1；（b） KT2；（c） KT3；（d） KT4

Fig 3. Topography, exploration boundaries and location of exploration holes：（a） KT1；（b） KT2；（c） KT3；（d） KT4

下载: 全尺寸图片幻灯片

图 4 矿体的品位信息：(a) KT1；(b) KT2；(c) KT3；(d) KT4

Fig 4. Ore body grade information: (a) KT1; (b) KT2; (c) KT3; (d) KT4

下载: 全尺寸图片幻灯片

图 5 KT1矿体勘探线方向角为0°时勘探孔网优化结果

Fig 5. Optimization results of KT1 orebody when the α = 0°

下载: 全尺寸图片幻灯片

图 6 勘探孔数量和设计储量随勘探线方向夹角α的变化情况：(a) 勘探孔数量；(b) 稀土储量

Fig 6. Number of exploration holes and designed reserves change with direction angle α of exploration line: (a) exploration holes; (b) rare earth reserves

下载: 全尺寸图片幻灯片

图 7 设计储量与勘探储量的相对误差（η）随勘探孔数量的变化情况：（a） KT1；（b） KT2；（c） KT3；（d） KT4

Fig 7. Relative error of designed reserves and explored reserves （η） varies with the number of exploration holes: （a） KT1; （b） KT2; （c） KT3; （d） KT4

下载: 全尺寸图片幻灯片

图 8 实际勘探结果的单位面积稀土质量分布云图：（a） KT1；（b） KT2；（c） KT3；（d） KT4

Fig 8. Cloud map of rare earth mass distribution per unit area of actual exploration results（a） KT1; （b） KT2; （c） KT3; （d） KT4

下载: 全尺寸图片幻灯片

图 9 单位面积稀土质量与勘探孔孔口高程平均曲率的关系：（a） KT1；（b） KT2；（c） KT3；（d） KT4

Fig 9. Relationship between rare earth mass per unit area and elevation of exploration holes: （a） KT1; （b） KT2; （c） KT3; （d） KT4

下载: 全尺寸图片幻灯片

图 10 实际勘探和优化设计的单位面积稀土质量的绝对误差分布云图：（a） KT1；（b） KT2；（c） KT3；（d） KT4

Fig 10. Cloud plot of absolute error distribution of rare earth mass per unit area for actual exploration and optimized design: （a） KT1; （b） KT2; （c） KT3; （d） KT4

下载: 全尺寸图片幻灯片

图 11 A-1、B-2和D-2区域勘探的基本参数：（a）平均品位；（b）矿层厚度；（c）单位面积稀土质量

Fig 11. Basic parameters for exploration in A-1, B-2 and D-2 areas: （a） average grade; （b） ore layer thickness; （c）mass of rare earths per unit area

下载: 全尺寸图片幻灯片

表 1 矿体的稀土配分

Table 1 Rare earth partitioning of ore body

矿体	La₂O₃	CeO₂	Pr₆O₁₁	Nd₂O₃	Sm₂O₃	Eu₂O₃	Gd₂O₃	Tb₄O₇	Dy₂O₃	Ho₂O₃	Er₂O₃	Tm₂O₃	Yb₂O₃	Lu₂O₃	Y₂O₃
KT1	17.50	4.15	5.29	18.51	3.89	0.72	3.92	0.97	3.90	0.93	2.60	0.22	2.03	0.05	35.32
KT2	20.09	2.38	4.29	17.61	4.03	0.77	4.96	0.67	5.29	0.91	2.62	0.33	2.31	0.33	33.42
KT3	18.61	5.88	4.56	15.87	4.08	0.59	4.34	0.76	5.00	0.93	2.78	0.38	2.33	0.34	33.53
KT4	17.74	3.09	5.44	17.72	4.28	0.80	4.78	0.81	4.67	0.95	3.08	0.40	2.18	0.30	33.76

下载: 导出CSV

表 2 矿体单位面积稀土质量与勘探孔孔口高程显著性的t检验

Table 2 A t-test for the significance of rare earth mass per unit area of ore body versus exploration hole aperture elevation

矿体		方差方程的Levene检验		均值方程的t检验
		F	显著性	t	df	显著性（双侧）	均值差值	标准误差值	差值的95%置信区间
		F	显著性	t	df	显著性（双侧）	均值差值	标准误差值	下限	上限
KT1	假设方差相等	5.032	0.026	-4.535	172.000	<0.001	-0.216	0.048	-0.310	-0.122
KT1	假设方差不相等	—	—	-4.535	161.981	<0.001	-0.216	0.048	-0.310	-0.122
KT2	假设方差相等	9.849	0.002	-4.301	186.000	<0.001	-0.212	0.049	-0.309	-0.115
KT2	假设方差不相等	—	—	-4.363	174.768	<0.001	-0.212	0.049	-0.308	-0.116
KT3	假设方差相等	25.360	<0.001	-9.952	120.000	<0.001	-0.757	0.076	-0.908	-0.607
KT3	假设方差不相等	—	—	-10.327	100.073	<0.001	-0.757	0.073	-0.903	-0.612
KT4	假设方差相等	23.272	<0.001	-8.944	215.000	<0.001	-0.202	0.025	-0.246	-0.157
KT4	假设方差不相等	—	—	-9.075	159.521	<0.001	-0.202	0.022	-0.245	-0.158
注：“—”代表无此数据。

下载: 导出CSV

参考文献(40)

[1]	池汝安, 刘雪梅. 风化壳淋积型稀土矿开发的现状及展望[J]. 中国稀土学报, 2019, 37(2): 129-140.
[2]	王猛, 徐旸, 赵龙胜, 等. 稀土采选冶绿色标准现状及发展趋势分析[J]. 中国稀土学报, 2022, 40(6): 1021-1031.
[3]	陈飞, 张仕彬, 谢蕴忠, 等. 离子型稀土堆浸场地复合土壤固化剂正交实验研究[J]. 有色金属科学与工程, 2023, 14(6): 887-894.
[4]	池汝安, 张臻悦, 余军霞, 等. 风化壳淋积型稀土矿研究进展[J]. 中国矿业大学学报, 2022, 51(6): 1178-1192.
[5]	HUANG Y, LONG P, WANG G S, et al. Ion-exchange model for the leaching process of ion-adsorption-type rare-earth ores considering the influence of anions[J]. Minerals, 2023, 13(12): 1475.
[6]	李琪, 秦磊, 王观石, 等. 离子吸附型稀土浸矿机制研究现状[J]. 中国稀土学报, 2021, 39(4): 543-554.
[7]	黄金, 杨幼明, 邓扬悟, 等. 硫酸镁浸出离子型稀土矿动力学研究[J]. 稀有金属, 2022, 46(2): 265-272.
[8]	HUANG Y, LONG P, WANG G S, et al. Decoupling method for the convective-dominated leaching process of ion-adsorption-type rare-earth ores[J]. Minerals, 2023, 13(1): 89.
[9]	秦磊, 王观石, 罗嗣海, 等. 离子型稀土矿浸矿剂用量计算模型[J]. 中国有色金属学报, 2019, 29(8): 1781-1789.
[10]	张子军, 瞿亮, 段文婷, 等. 赣南钻在滇西南离子吸附型稀土矿勘查中的应用[J]. 稀土, 2022, 43(4): 100-109.
[11]	谢有炜, 漆富勇, 阙兴华, 等. 浅谈离子吸附型稀土矿勘查的有关问题[J]. 稀土, 2018, 39(6): 122-128.
[12]	梅晓仁, 张瑞新, 高永胜. 地质统计学法在露天矿勘探网度优化中的应用[J]. 中国矿业大学学报, 2003, 32(4): 121-123.
[13]	HOSSEIN M A, MEMARIAN H. A novel algorithm for designing the layout of additional boreholes[J]. Ore Geology Reviews, 2015, 67: 34-42.
[14]	ANAM N K, BONG W K, ATIF R, et al. A new method for determination of optimal borehole drilling location considering drilling cost minimization and sustainable groundwater management[J]. ACS Omega, 2023, 8(12): 10806-10821.
[15]	ZHOU Y, CHEN X, WU M, et al. A novel optimization method for geological drilling vertical well[J]. Information Sciences, 2023, 634: 550-563.
[16]	SOLTANI S, HEZARKHANI A, ERHAN T A, et al. Use of genetic algorithm in optimally locating additional drill holes[J]. Journal of Mining Science, 2011, 47(1): 62-72.
[17]	MARCIN C. Optimal placement of two soil soundings for rectangular footings[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(3): 603-611.
[18]	黄豪. 离子型稀土矿品位空间分布变异函数的自适应选择算法[J]. 福建冶金, 2023, 52(3): 1-4.
[19]	王明照, 龙平, 胡世丽, 等. 一种离子型稀土矿体渗透性空间分布的计算方法[J]. 有色金属科学与工程, 2023, 14(2): 280-287.
[20]	AHSAN N, SCHEDING S, MONTEIRO S T, et al. Adaptive sampling applied to blast-hole drilling in surface mining[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 75: 244-255.
[21]	张鸿刚, 李成名, 殷勇, 等. 一种改进的曲线特征点提取方法[J]. 测绘科学, 2020, 45(3): 128-134.
[22]	王长虹, 朱合华, 钱七虎. 克里金算法与多重分形理论在岩土参数随机场分析中的应用[J]. 岩土力学, 2014, 35(增刊2): 386-392.
[23]	强新刚. 兰渝线太公车站边坡工程滑坡分析[J]. 铁道工程学报, 2013, 30(6): 22-25,58.
[24]	自然资源部矿产资源保护监督司, 自然资源部矿产资源储量评审中心. 矿产资源储量技术标准汇编(上册)[M].2版.北京: 地质出版社, 2021.
[25]	江西省市场监督管理局. DB36/T 1158-2019. 风化壳离子吸附型稀土矿产地质勘查规范[S]. 南昌:江西省自然资源厅, 2019.
[26]	池汝安, 田君. 风化壳淋积型稀土矿化工冶金[M]. 北京:科学出版社, 2006.
[27]	刘胜楠,刘文君,邹国华. 基于倾向值匹配的干扰数据检测方法[J]. 系统科学与数学, 2022, 42(1): 153-174.
[28]	周吕,李青逊,权菲, 等. 基于无人机倾斜摄影测量的矿产储量动态监测[J]. 科学技术与工程, 2022, 22(5): 1760-1767.
[29]	肖笛, 黄天海, 张本健, 等. 四川盆地南部向斜区二叠系岩溶孔隙型石灰岩储层成因与天然气勘探新领域[J]. 天然气工业, 2024, 44(2): 52-67.
[30]	胡世丽,黄颖,王观石, 等. 赣南信丰风化壳淋积型稀土矿的吸附特性[J]. 中国稀土学报, 2017, 35(6): 807-814.
[31]	王枭, 陈双敏, 陈叶芳, 等. 基于模板采样和MLS能量函数的曲率计算[J]. 计算机辅助设计与图形学学报, 2015, 27(6): 1104-1109.
[32]	刘进. 子流形平均曲率向量场的线性相关性[J]. 数学学报, 2013,56(5): 669-686.
[33]	廖昕,彭作祥. 独立非同分布二元高斯三角阵最大值的渐近性及相关统计推断[J]. 数学学报, 2017, 60(2): 297-314.
[34]	JURKOVÁ V, ŽEŽULA I, KLEIN D, et al. Unbiased estimator of correlation coefficient[J]. Communications in Statistics - Theory and Methods, 2022, 51(1): 95-115.
[35]	WANG G, MUSCHELLI J, LINDQUIST M A. Moderated t-tests for group-level fMRI analysis: NeuroImage[J]. NeuroImage, 2021, 237: 118141.
[36]	范雷,黄正加,周火明, 等. 考虑中间主应力的原位岩体强度参数取值研究[J]. 岩石力学与工程学报, 2016, 35(A1): 2682-2686.
[37]	马利群,秦奋,孙九林, 等. 黄土高原昼夜不对称性增温及其对植被NDVI的影响[J]. 资源科学, 2018, 40(8): 1684-1692.
[38]	姚清华, 林虬, 颜孙安, 等. 基于稀土元素指纹分析判别安溪铁观音和华安铁观音的研究[J]. 现代食品科技, 2017, 33(4): 295-299.
[39]	罗磊,邢海峰,王松涛. 基于机器学习的单孔绝热气膜冷却效率分布预测研究[J]. 推进技术, 2022, 43(4): 218-228.
[40]	卢峻达,许林云,杭晓晨, 等. 基于有限元法的BF142型刨花振动筛结构强度分析[J]. 林业工程学报, 2022, 7(1): 145-152.

施引文献

资源附件(0)

图(11) / 表(2)

计量

文章访问数: 7
HTML全文浏览量: 2
PDF下载量: 2
被引次数: 0

1 算法模型的基本原理及评价方法
1.1 双向长短期记忆网络
1.2 自注意力机制
1.3 Bi-LSTM与SA融合模型
1.4 模型评价指标
2 工程案例分析
2.1 工程概况
2.2 Bi-LSTM-SA融合模型的应用
3 结论

风化壳淋积型稀土矿勘探网度优化的特征点法

通讯作者: 龙 平（1992— ）,博士,讲师,主要从事离子型稀土资源绿色提取等方面的研究工作。E-mail：longp1234@163.com

计量

出版历程

Characteristic point method for optimizing exploration network of weathered crust elution-deposited rare earth ore

1 算法模型的基本原理及评价方法

1.1 双向长短期记忆网络

1.2 自注意力机制

1.3 Bi-LSTM与SA融合模型

1.4 模型评价指标

2 工程案例分析

2.1 工程概况

2.2 Bi-LSTM-SA融合模型的应用

3 结 论

计量

出版历程

目录

1 算法模型的基本原理及评价方法

1.1 双向长短期记忆网络

1.2 自注意力机制

1.3 Bi-LSTM与SA融合模型

1.4 模型评价指标

2 工程案例分析

2.1 工程概况

2.2 Bi-LSTM-SA融合模型的应用

3 结 论

通讯作者:
龙平（1992—　）,博士,讲师,主要从事离子型稀土资源绿色提取等方面的研究工作。E-mail：longp1234@163.com

3 结论

3 结论