多台阶高陡岩质边坡的稳定性问题一直是地质工程领域的研究热点之一^[1]。这类边坡常见于矿山开采、道路建设以及水库工程中,因其特殊的地质条件和施工环境,极易受到爆破与自然风化的影响,而导致其发生变形破坏^[2]。爆破作为岩体掘进过程中不可或缺的技术手段,虽然可以有效地促进工程进度,但也不可避免地对边坡岩体结构产生扰动,使得岩体内原有的力学平衡被打破^[3]。与此同时,自然风化过程长期作用于岩质边坡表面,导致岩石物理力学性能逐渐劣化,从而加剧了边坡的不稳定性^[4-6]。在爆破与自然风化的共同作用下,边坡变形发展成为一个复杂的动态过程,进而诱发一系列地质灾害,如滑坡、崩塌和泥石流等,不仅威胁着工程安全,还对周边环境和人类活动造成了严重的威胁^[7]。例如,1963年意大利北部瓦伊昂水库附近的山体发生大规模滑坡,造成了约2 000人死亡^[8]；2008年汶川地震引发了一系列山体滑坡与崩塌,这些次生灾害进一步加剧了灾情的严重性^[9]。

通过高精度地对边坡变形趋势的预测,可以为边坡工程的安全设计和灾害预警提供科学依据,从而有效地预防地质灾害的发生,保障人员及工程的安全^[8-12]。目前,常用的传统变形预测方法包括物理模型实验、数值模拟和统计分析等^[13-17]。这些方法虽然在一定程度上能够反映边坡变形的趋势,但也存在着显著的不足^[18-20]。物理模型实验受限于实验条件,难以全面反映实际边坡的复杂性；数值模拟方法则依赖于边坡模型参数的准确性,而这些参数往往难以通过现场测试精确获取；统计分析方法在处理非线性和时变特性明显的边坡变形数据时,预测精度较低,难以满足实际工程的需求。

为克服传统方法的不足,深度学习在处理时间序列问题能力备受关注,其中主要包括GRU、LSTM、Bi-LSTM、BERT和Transformer等模型。相较于LSTM模型,GRU模型具有更少的参数,但其在处理复杂长序列数据时,效果通常不如LSTM和Bi-LSTM模型,在边坡变形预测过程中,下一时刻位移变形不仅依赖于历史数据,还会受到天气、爆破等因素的干扰,而LSTM模型只能捕捉到前向依赖关系,无法充分利用时间序列中的所有信息。BERT模型复杂且资源消耗较大,训练与推理成本较高,更擅于长文本分类、系统问答等任务,对时间序列预测任务处理能力一般。Transformer模型在处理大规模数据与高并发任务时表现出色,但对于边坡变形预测这种数据量相对较少的任务,发挥不了其优势,且其对计算资源需求巨大。相较于其他的时间序列建模方法,Bi-LSTM-SA（Bidirectional Long Short-Term Memory Self-Attention）融合模型结合了双向长短期记忆网络（Bi-LSTM）与自注意力机制（SA）的优势,能够有效地捕捉边坡变形数据中的时序特征和全局依赖关系。双向长短期记忆网络则通过前向和后向2个方向的信息传播,提高了模型对边坡变形数据的预测精度,自注意力机制通过计算输入序列中各元素之间的相关性,增强了模型对重要特征的识别能力。因此,Bi-LSTM-SA融合模型在处理非线性、时变性强、时序关联性及高维性的边坡变形数据方面具有显著的优势,能够提供更加精准和可靠的变形预测结果,该模型已被广泛地应用在故障诊断^[21]、仪器设备剩余寿命预测^[22]及时间序列预测^[23]等领域。

综上所述,本研究旨在通过Bi-LSTM-SA融合模型的应用,提高多台阶高陡岩质边坡变形预测的精度和可靠性,为边坡工程的安全设计和地质灾害预警提供技术支持,具有重要的理论意义和实际价值。

1   算法模型的基本原理及评价方法

1.1   双向长短期记忆网络

LSTM模型通过引入门控机制解决了标准RNN模型在处理长序列时梯度消失和梯度爆炸的问题。LSTM模型的基本结构包括输入门、遗忘门、输出门以及一个细胞状态^[24]。

1）输入门：其功能可以分2个部分。一部分是判断当前输入信息的重要程度,确定需要更新的细胞状态,另一部分是把需要更新的信息传入细胞状态,完成对细胞状态的更新。

输入门在t时刻的输出结果如式（1）所示：

新的候选细胞状态如式（2）所示：

式（1）、式（2）中：$\sigma$表示激活函数；$W_i$与$W_C$分别表示输入门确定细胞状态的权重系数与更新细胞状态的权重系数；$b_i$与$b_C$分别表示输入门确定细胞状态的偏置项与更新细胞状态的偏置项；$\mathrm{t}\mathrm{a}\mathrm{n}h$表示激活函数。输入门根据当前输入信息$x_t$与上一时刻的隐藏层状态$h_{t-\mathrm{1}}$。

2）遗忘门：其功能是根据输入门的输出结果,判断模型中细胞状态所要丢弃与保留的信息。遗忘门的计算方程如式（3）所示：

式（3）中：$x_t$表示t时刻的输入数据；$f_t$表示遗忘门的计算结果；$h_{t-\mathrm{1}}$表示隐藏层状态；$\sigma$表示遗忘门的激活函数；$W_f$表示遗忘门的权重系数；$b_f$表示遗忘门的偏置项。

3）细胞状态：结合输入门的输出结果与遗忘门计算结果,对细胞状态进行更新,而细胞状态就是LSTM神经网络保留长期记忆的地方。细胞状态更新过程如式（4）所示：

式（4）中：$f_t$表示遗忘门在t时刻的输出结果；$C_{t-\mathrm{1}}$表示细胞状态在t-1时刻的长时记忆输入；${\tilde{C}}_t$表示细胞状态在t-1时刻的候选值；$i_t$表示输入门在t时刻的输出结果。

4）输出门：根据细胞状态更新结果计算对隐藏层状态的影响,并结合输出门的输出结果与细胞状态信息更新隐藏层状态。输出门计算公式如式（5）、式（6）所示：

式（5）、式（6）中：$o_t$表示输出门在时刻t的输出结果；$h_t$表示短时记忆的输出结果。

Bi-LSTM是一种改进的RNN,Bi-LSTM网络模型是通过同时训练2个LSTM网络,包含一个正向LSTM网络（从前到后处理序列的能力）和一个反向LSTM网络（从后到前处理序列的能力）,通过在正向和反向2个方向上处理序列数据,进而实现对时间序列数据中前后信息的依赖关系捕捉,如图1所示。每个时间步的输出都由正向LSTM与反向LSTM的隐藏状态拼接而成。现假设输入序列为$\{x_{\mathrm{1}},x_{\mathrm{2}},\cdots ,x_t\}$,则Bi-LSTM计算过程如下。

图  1  Bi-LSTM算法流程

Figure  1.  Flowchart of Bi-LSTM algorithm

下载: 全尺寸图片 幻灯片

1）正向LSTM计算：$h_t=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}(x_t,h_{t-\mathrm{1}},C_{t-\mathrm{1}})$；

2）反向LSTM计算：$h_t=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}(x_t,h_{t+\mathrm{1}},C_{t+\mathrm{1}})$；

3）合并输出：将正向LSTM和反向LSTM的输出进行拼接或加权平均,得到时间序列数据的综合表示。

1.2   自注意力机制

SA（Self-Attention）网络是一种常被用于序列数据的处理,它通过计算输入序列中每个元素与其他所有元素之间的相关性,从而捕捉序列数据中的全局依赖关系。SA网络的优势在于,它能够并行处理序列数据,克服了传统RNN在处理长序列时的计算效率低下问题,同时,SA网络还能够有效地关注序列中的重要信息,提升模型的预测精度。SA网络主要包括以下几个步骤：

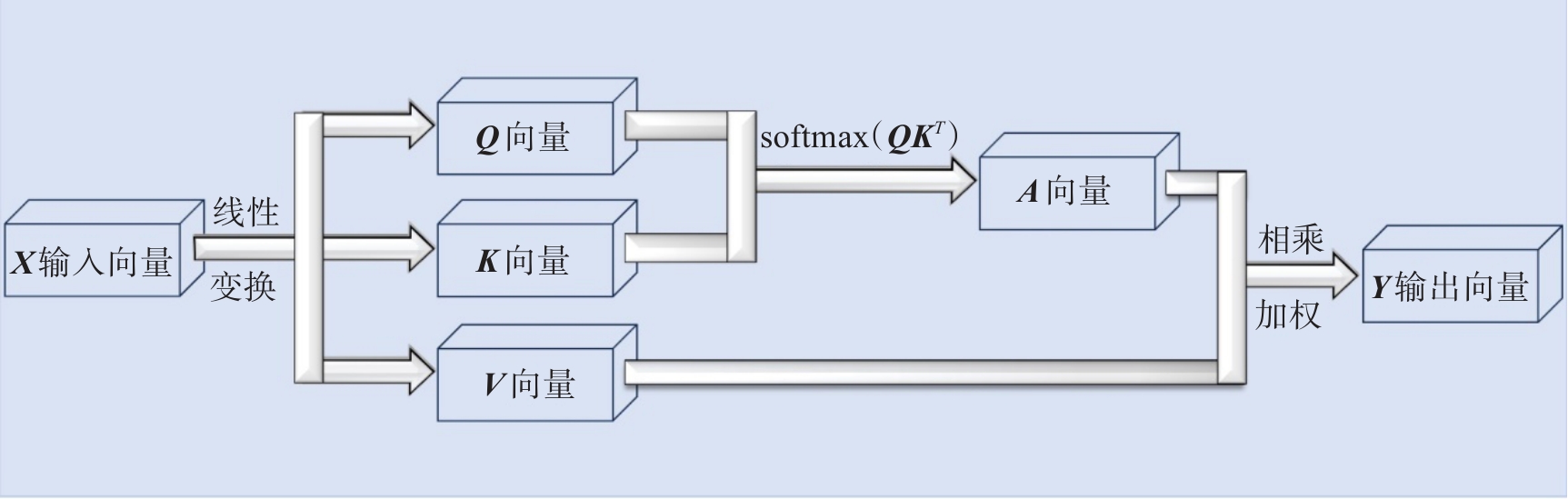
1）Query, Key, Value 体系：自注意力机制主要通过查询（Query）、键（Key）和值（Value）3个向量来运作,对输入序列中的每个元素进行不同的线性变换,产生一个Query向量、一个Key向量和一个Value向量,如图2所示。

图  2  自注意力机制算法流程

Figure  2.  Flow chart of self-attention mechanism algorithm

下载: 全尺寸图片 幻灯片

2）注意力分数计算：对于输入序列数据中第i个元素,它与输入序列数据中第j个元素之间的注意力分数$scor{e}_{ij}$,可以通过Q向量与K向量通过计算得到,计算公式如式（7）所示：

式（7）中：$d_k$表示K向量的维度；缩放因子$d_k$对于稳定softmax函数的梯度具有重要意义。

3）计算权重分配：将注意力分数计算结果通过softmax函数转换为概率分布数据,并将其作为各个元素的注意权重$a_{ij}$,计算过程如式（8）所示：

4）加权求和：利用注意力权重对输入序列进行加权求和,得到序列的注意力表示,计算过程如式（9）所示：

式（9）中：$Contex{t}_i$表示第i元素的注意力。

1.3   Bi-LSTM与SA融合模型

Bi-LSTM-SA模型结合了Bi-LSTM网络与SA网络的优势,用于预测多台阶高陡岩质边坡的变形。该模型通过Bi-LSTM捕捉序列中的前后文信息,并通过SA捕捉全局依赖关系,从而实现对多台阶高陡边坡变形的高精度预测。

Bi-LSTM与SA融合模型架构如下：

数据预处理：将日降雨量$R=[r_{\mathrm{1}},r_{\mathrm{2}},\cdots ,r_T]$、蒸发量$E=[e_{\mathrm{1}},e_{\mathrm{2}},\cdots ,e_T]$、炸药用量$N=[n_{\mathrm{1}},n_{\mathrm{2}},\cdots ,n_T]$、监测点与爆破点之间距离$L=[l_{\mathrm{1}},l_{\mathrm{2}},\cdots ,l_T]$进行归一化处理（T表示时刻）,并将其划分为训练集和验证集,输入特征向量为${\mathit{X}}_t=[{\mathit{R}}_t,{\mathit{E}}_t,{\mathit{N}}_t,{\mathit{L}}_t,{\mathit{c}}_t]$,${\mathit{c}}_t$表示t时刻累计位移量,训练集数据为$[{\mathit{X}}_t,{\mathit{c}}_{t+\mathrm{1}}]$。

Bi-LSTM层：通过双向LSTM单元,分别在正向和反向上处理嵌入向量,得到正向和反向的LSTM输出。正向LSTM计算如下：

反向LSTM计算如下：

Bi-LSTM输出为正向与反向输出的拼接：

SA层：利用自注意力机制计算Bi-LSTM输出结果中的注意力权重,增强模型对重要时间步的关注,计算注意力权重并对隐藏状态进行加权。

计算加权隐藏层状态：

式（13）中：${\alpha }_t$表示注意力权重系数。

融合层：将Bi-LSTM输出的隐藏状态与Self-Attention机制输出的加权隐藏状态进行融合,最终的融合特征如式（14）：

输出层：通过全连接层将融合后的特征表示映射到目标输出${\mathit{c}}_{t+\mathrm{1}}$,即下一时刻的累计位移量。

式（15）中：$\sigma$表示激活函数；W表示全连接层的权重系数；b表示全连接层的偏置。

根据日降雨量、日蒸发量、炸药用量与监测点与爆破点之间距离等环境因素对边坡变形的影响,以及边坡变形监测数据构成时间序列,利用Bi-LSTM-SA融合模型提取输入时间序列之间的相互依赖关系,实现对多台阶高陡岩质边坡变形的预测。

1.4   模型评价指标

为了评价基于Bi-LSTM-SA融合模型的多台阶高陡边坡变形预测,本文选用方根误差（RMSE）、平均绝对误差（MAE）及决定系数（R²）3个指标对模型进行评价。其中,RMSE、MAE与R²的计算公式如式（16）、式（17）、式（18）所示：

式（16）—式（18）中：m表示数据集样本总数；$f(x_i)$表示Bi-LSTM-SA融合模型的预测数据；$y_i$表示多台阶高陡边坡变形测量数据；$\overline{y}$表示多台阶高陡边坡变形测量数据的均值。决定系数用于评价模型预测数据与实测数据的相关性,其取值范围分布在0到1区间内,R²数值越大,表明Bi-LSTM-SA融合模型的预测效果越好。

2   工程案例分析

2.1   工程概况

本文以我国华东地区某露天矿山多台阶高陡岩质边坡为研究对象,台阶高度约为15 m,边坡角度约为70°,边坡由多个台阶组成,每个台阶的高度与边坡角度略有不同,边坡形貌如图3所示。多台阶高陡岩质边坡具有复杂的地质与几何特征,其稳定性受到降雨量、蒸发量及爆破扰动等多种因素的影响,通过合理地监测,可以有效地预防边坡失稳,保障露天矿山安全高效地开采。项目采用全站仪和GNSS技术相结合的方法,利用高精度全站仪对表面设定的监测点进行周期性观测,结合GNSS观测数据及全站仪测量数据,获取监测点的高精度三维坐标。

该边坡主要由软弱与半坚硬岩石组成,风化程度相对较高,呈破碎状结构,局部呈散体结构,整体强度相对较低,工程性能相对较差,在自然环境与爆破振动扰动共同作用下易发生滑坡等地质灾害,如图4所示。在边坡的关键位置（如台阶顶、台阶底、坡面中部）布设监测点,确保监测点布设均匀,覆盖整个监测区域,并且选择稳定的基准点作为参照点,基准点应远离监测区域。对露天采场北区、东区及南区建立了GNSS与全站仪监测点,监测网布设监测点40个,并建立2个基站和1个CORS站,建立了一套集监测数据自动化采集、传输及可视化呈现为一体的变形监测系统。

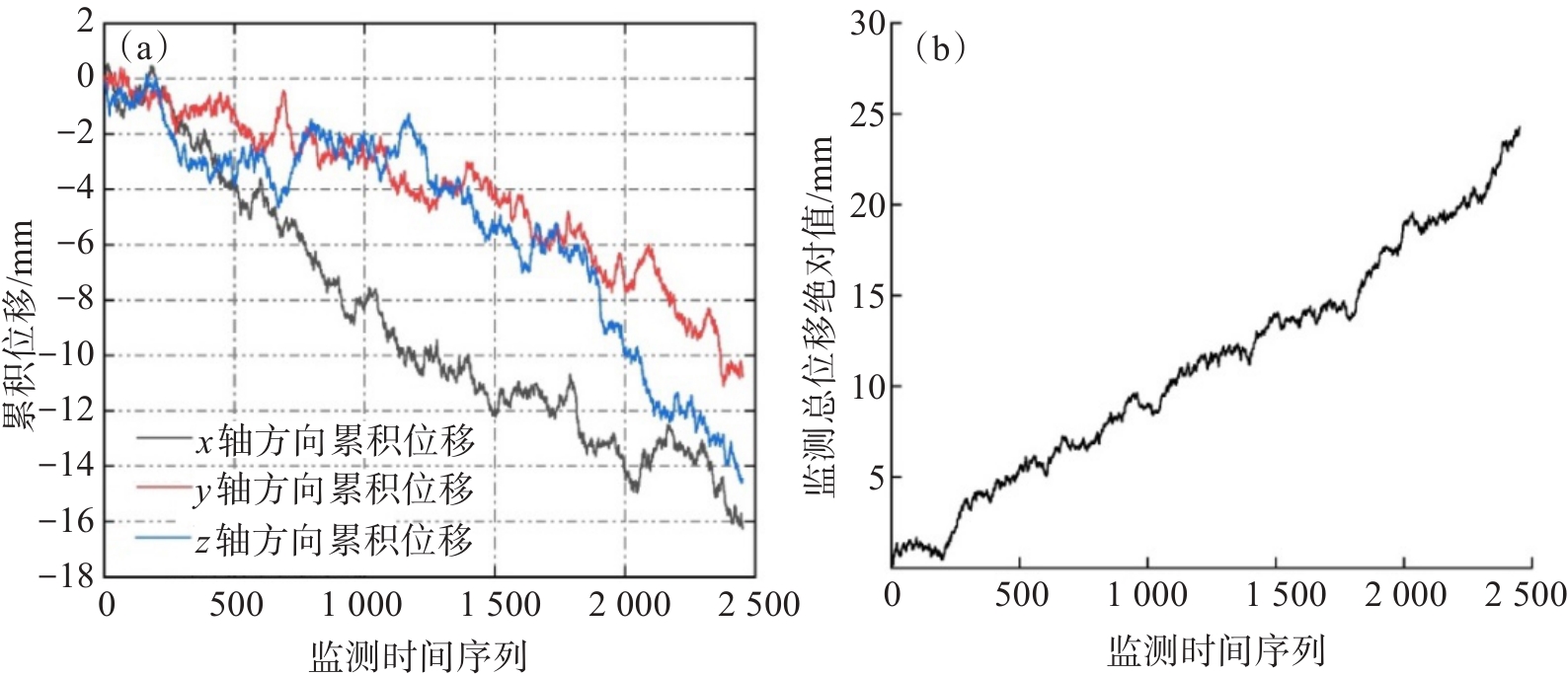
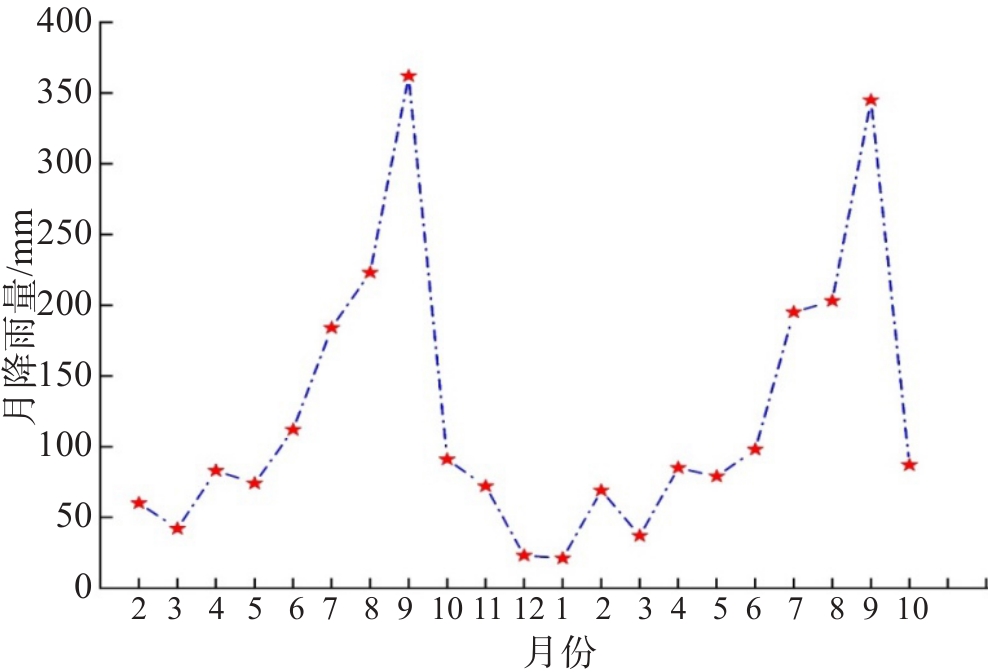
通常情况下各GNS与全站仪监测点每6 h测量一次,但在极端天气条件下GNS与全站仪监测点可以实现每5 min测量一次。利用Bi-LSTM-SA模型对所有监测点变形数据进行分析,发现各监测点的预测准确率较为接近,限于篇幅原因,本文随机选择了一个监测点数据进行了展示,设置每6 h对边坡数据进行采集一次,以2021年2月26日至2022年10月4日期间的监测数据为研究对象,共获得了2 452组监测数据,对上述数据进行预测分析。现以正北方向规定为x轴,正东方向规定为y轴,竖直方向规定为z轴方向,每个方向的累积监测位移如图5所示。监测区域2021年2月至2022年10月的降雨量统计结果如图6所示,降雨主要集中在每年的6—9月期间,最大月降雨量为362 mm。

图  5  监测点位移监测数据： （a）各方向监测数据；（b）监测总位移量数据

Figure  5.  Displacement monitoring data of monitoring points： （a） monitoring data in all directions； （b） monitoring of total displacement data

下载: 全尺寸图片 幻灯片

图  6  监测期间月降雨量统计

Figure  6.  Monthly rainfall statistics during the monitoring period

下载: 全尺寸图片 幻灯片

2.2   Bi-LSTM-SA融合模型的应用

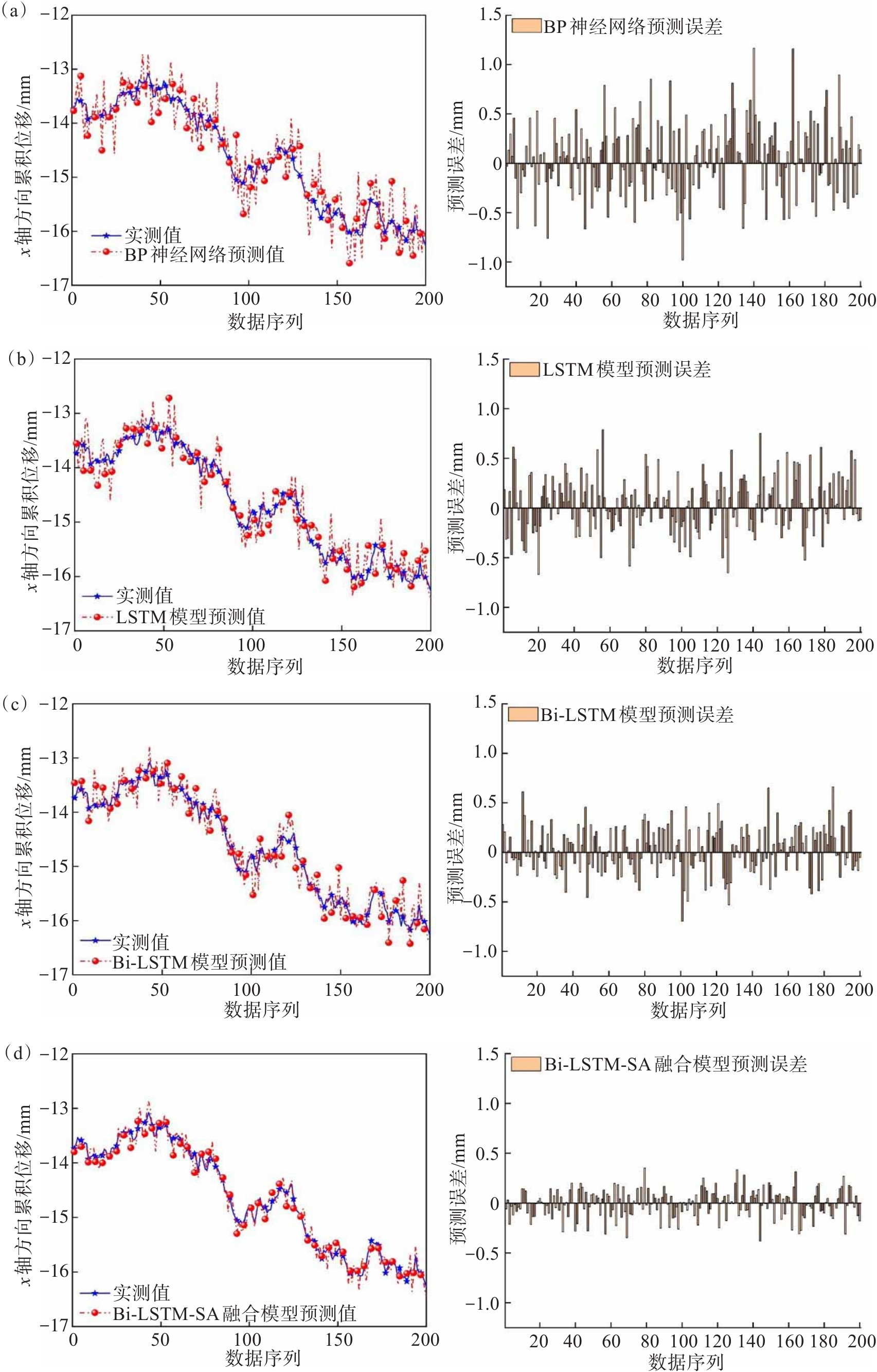
对监测数据进行预处理,将预处理后数据的前2 252组数据作为训练集,后200组数据作为测试集。利用Bi-LSTM-SA融合模型对训练集数据进行训练,使用均方误差作为损失函数,使用Adam优化器对Bi-LSTM-SA融合模型进行优化。为了验证Bi-LSTM-SA融合模型对台阶高陡边坡变形预测的准确性,将Bi-LSTM-SA融合模型的预测结果与BP神经网络、LSTN模型、Bi-LSTM模型的预测结果进行对比分析,同时将上述模型的预测结果与实测数据进行验证,验证本文提出Bi-LSTM-SA融合模型的可行性。

由图7可知：在相同输入参数条件下,相较于BP神经网络、LSTM模型与Bi-LSTM模型预测结果,Bi-LSTM-SA融合模型对多台阶高边坡在正南方的变形预测结果整体预测误差更小,同时Bi-LSTM-SA融合模型的预测结果与实测结果更为接近,验证了Bi-LSTM-SA融合模型在多台阶高陡边坡变形预测中的可行性。

图  7  x轴方向不同模型预测结果：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure  7.  Prediction results of different models in x-axis direction: (a) BP neural network; (b) LSTM model ; (c) Bi-LSTM model; (d) Bi-LSTM-SA fusion model

下载: 全尺寸图片 幻灯片

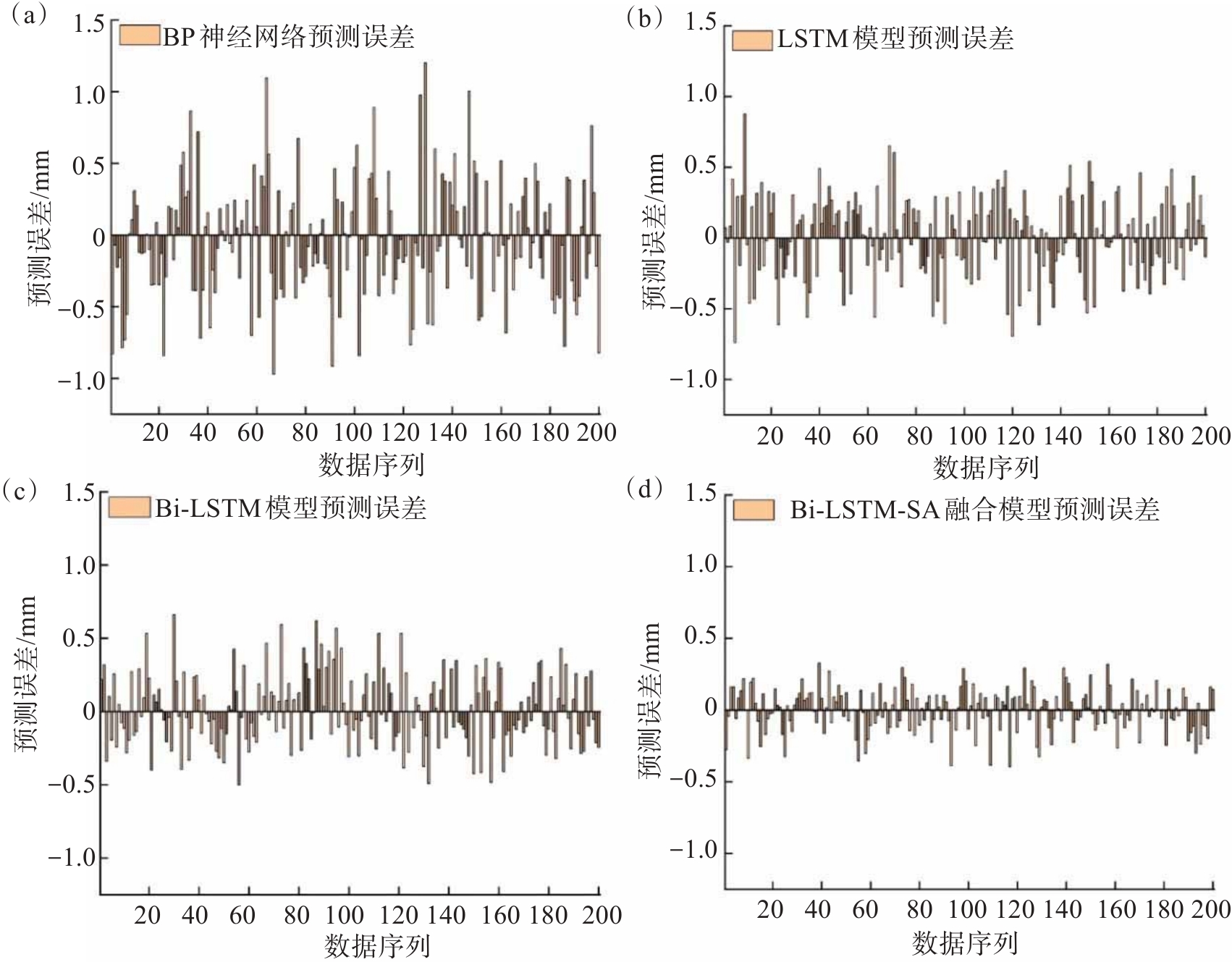
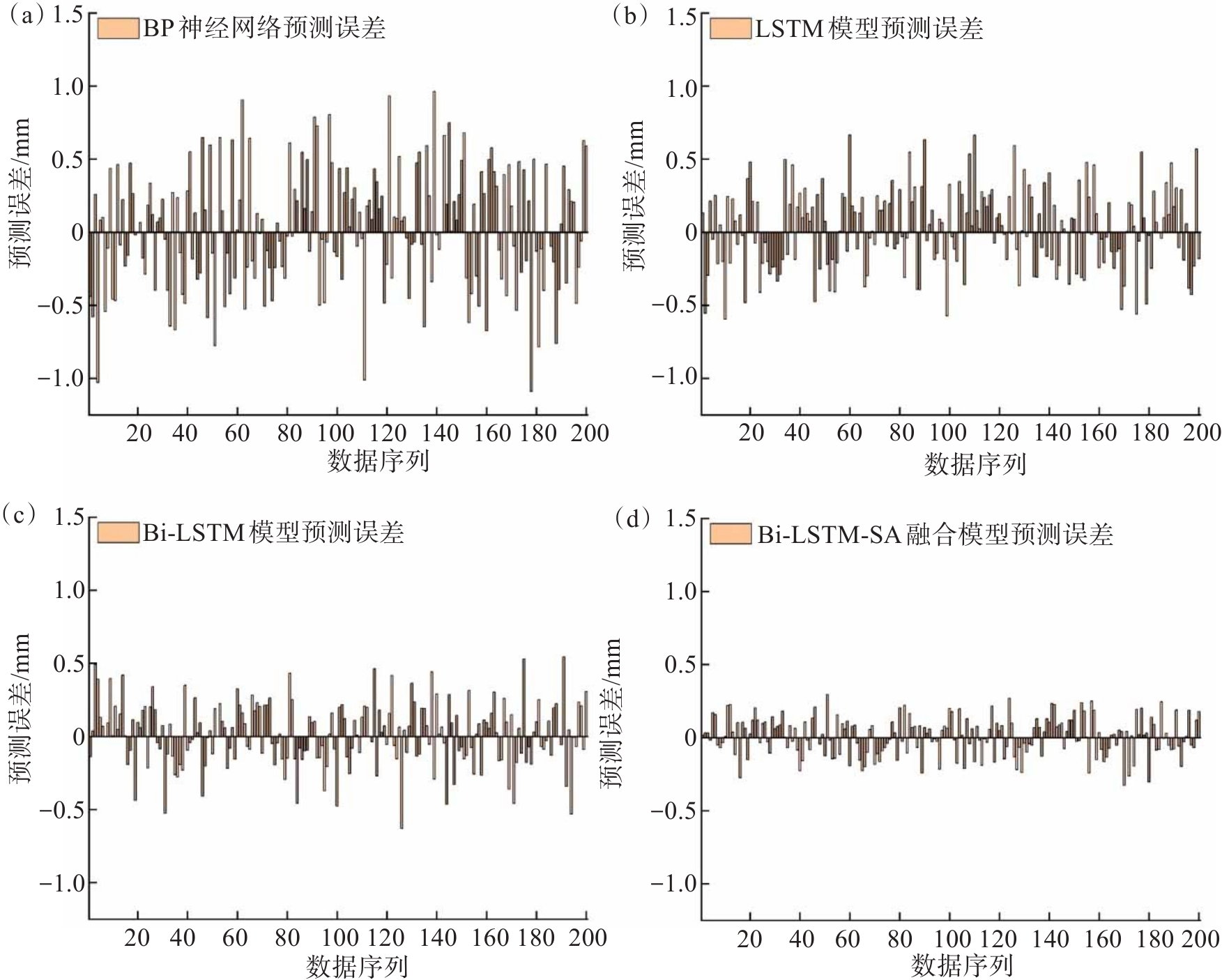
为了进一步验证Bi-LSTM-SA融合模型对多台阶高陡边坡变形预测的有效性,并提高预测效果的可靠性,本文对测试集数据的y轴与z轴方向预测误差进行了统计分析,如图8与图9所示。并对测试集的RMSE、MAE及R²进行了统计分析,如表1—表3所列,进而实现对不同模型预测性能进行分析。

图  8  y轴方向不同模型预测误差：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure  8.  Prediction errors of models with different y-axis directions：（a） BP neural network；（b） LSTM model；（c） Bi-LSTM model；（d） Bi-LSTM-SA model

下载: 全尺寸图片 幻灯片

图  9  z轴方向不同模型预测误差：（a） BP神经网络；（b） LSTM模型；（c） Bi-LSTM模型；（d） Bi-LSTM-SA融合模型

Figure  9.  Prediction errors of models with different z-axis directions：（a） BP neural network ；（b） LSTM model；（c） Bi-LSTM model；（d） Bi-LSTM-SA model

下载: 全尺寸图片 幻灯片

表  1  不同模型在x轴方向变形预测性能评价

Table  1.  Evaluation of deformation prediction performance of different models in x-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.377 7	0.297 5	0.250 0	0.148 4
MAE	0.300 5	0.242 8	0.206 4	0.120 5
R2	0.836 8	0.895 0	0.912 9	0.959 4

下载: 导出CSV 

| 显示表格

表  2  不同模型在y轴方向变形预测性能评价

Table  2.  Evaluation of deformation prediction performance of different models in y-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.420 1	0.291 5	0.263 1	0.167 5
MAE	0.327 8	0.235 2	0.214 1	0.137 8
R2	0.810 4	0.908 7	0.915 7	0.959 9

下载: 导出CSV 

| 显示表格

表  3  不同模型在z轴方向变形预测性能评价

Table  3.  Evaluation of deformation prediction performance of different models in z-axis direction

参数	BP神经网络	LSTM模型	Bi-LSTM模型	Bi-LSTM-SA融合模型
RMSE	0.391 2	0.325 7	0.254 2	0.168 2
MAE	0.317 9	0.261 4	0.202 7	0.135 4
R2	0.835 6	0.886 0	0.916 4	0.946 9

下载: 导出CSV 

| 显示表格

由图8、图9及表1—表3对比分析可知：BP神经网络的预测误差在-1~1.5 mm,最大值为1.42 mm, 3个方向预测结果的误差RMSE最大值为0.420 1,MAE最大值为0.327 8,R²最小值为0.810 4；LSTM模型的预测误差在-1~1 mm,最大值为0.95 mm,3个方向预测结果的误差RMSE最大值为0.325 7,MAE最大值为0.261 4,R²最小值为0.886 0；Bi-LSTM模型的预测误差在-0.75~0.75 mm,最大值为0.72 mm,3个方向预测结果的误差RMSE最大值为0.263 1,MAE最大值为0.214 1,R²最小值为0.912 9；Bi-LSTM-SA融合模型的预测误差在-0.5~0.5 mm,最大值为0.38 mm,3个方向预测结果的误差RMSE最大值为0.168 2,MAE最大值为0.137 8,R²最小值为0.946 9。实验结果表明,Bi-LSTM-SA融合模型预测结果能够与实测结果较好地拟合,较为准确地预测多台阶高陡边坡监测点3个方向的位移变化情况。

上述实验结果对比分析也表明了Bi-LSTM-SA融合模型不仅有较强的预测性能,也具有较好的可行性。

3   结 论

本文采用不同预测模型对多台阶高陡边坡监测点3个方向的位移变化进行了分析,并通过方根误差、平均绝对误差及决定系数3个指标对预测模型性能进行了评价,以我国华东地区某一多台阶高陡边坡监测数据为研究对象,对监测点3个方向的累积位移进行了预测,得到了以下结论：

1）在相同的输入条件下,相较于BP神经网络、LSTM模型与Bi-LSTM模型预测结果,Bi-LSTM-SA融合模型对多台阶高边坡在3个监测方向的变形预测结果整体预测误差更小,同时Bi-LSTM-SA融合模型的预测结果与实测结果更为接近。

2）将日降雨量、日蒸发量、炸药用量及监测点与爆破点之间的距离及日位移量等因素影响作为输入数据,考虑了自然风化与爆破扰动共同作用下多台阶高陡边坡变形特点,构建的Bi-LSTM-SA融合预测模型。Bi-LSTM-SA融合模型预测性能更强,而且还表现出了更好的稳定性与鲁棒性。

3）为了更为有效地指导露天矿山边坡的安全管理,后期应当更加充分地利用监测数据与Bi-LSTM-SA融合模型,实现对复杂环境条件下多台阶高陡边坡变形的有效预测,为边坡滑坡等地质灾害的预警工作提供技术支持。