选区激光熔化拱形点阵力学性能影响及优化

潘文瀚; 许明三; 韦铁平; 叶建华; 朱峰立; 杨林沂

doi:10.13264/j.cnki.ysjskx.2025.01.006

选区激光熔化拱形点阵力学性能影响及优化

潘文瀚^{1, 2},
许明三^1, ,,
韦铁平^{1, 2},
叶建华^{1, 2},
朱峰立^{1, 2},
杨林沂^{1, 2}

1.
福建理工大学,福建省智能加工技术及装备重点实验室,福州350118
2.
福建理工大学,机械与汽车工程学院,福州350118

基金项目:

国家自然科学基金资助项目 51575110

福建省自然科学基金资助项目 2020J01872

详细信息

通讯作者:
许明三（1974—　）,教授,主要从事激光增材制造、硬脆材料加工技术研究。E-mail：xums368@163.com

计量
- 文章访问数: 11
- HTML全文浏览量: 1
- PDF下载量: 1
出版历程
- 收稿日期: 2023-08-17
- 修回日期: 2024-02-19
- 刊出日期: 2025-02-27

Effect and optimization of mechanical properties of selected laser melting arch lattice

PAN Wenhan^{1, 2},
XU Mingsan^1, ,,
WEI Tieping^{1, 2},
YE Jianhua^{1, 2},
ZHU Fengli^{1, 2},
YANG Linyi^{1, 2}

1.
Fujian Key Laboratory of Intelligent Machining Technology and Equipment, Fujian University of Technology,Fuzhou350118, China
2.
School of Mechanical & Automotive Engineering, Fujian University of Technology,Fuzhou350118, China

摘要

摘要:
为提高轻量化前提下选区激光熔化成型点阵结构力学性能,融入拱形特征进行点阵结构设计。综合考虑多结构参数的交互影响,利用响应面法建立了拱形高跨比、单胞杆径和胞元高度3个结构参数与点阵弹性模量及抗压强度的数学关系模型,分析了结构参数对点阵弹性模量与抗压强度的影响规律,获得较优的结构参数组合。结果表明,拱形高跨比对结构弹性模量与抗压强度的影响最显著,随着高跨比的增大,结构弹性模量与抗压强度显著提高。优化得出拱形点阵的较优结构参数组合为拱形高跨比0.7、单胞杆径1.2 mm、胞元高度4.5 mm,在此条件下其弹性模量为2.012 GPa,抗压强度为79.254 MPa,相比优化前弹性模量和抗压强度分别提升21.57%和35.60%,结构力学性能显著增强。本研究可为轻量化点阵结构的设计与优化提供参考。
- 选区激光熔化 /
- 结构参数 /
- 拱形点阵 /
- 弹性模量 /
- 抗压强度
Abstract:
To enhance the mechanical properties of the lattice structure formed by selective laser melting under the premise of lightweight, the arch feature was incorporated into the lattice structure design. Considering the combined effects of various structural parameters, a mathematical relationship model of arch height-to-span ratio, strut diameter and cell height with lattice elastic modulus and compressive strength was established by response surface test. The impact of these structural parameters on the elastic modulus and compressive strength was analyzed and an optimal combination of parameters was determined. The findings reveal that the arch height-to-span ratio has the most significant influence on the elastic modulus and compressive strength of the structure. As the arch height-to-span ratio increases, both the elastic modulus and compressive strength of the structure demonstrate notable improvements. The optimal structural parameter combination of the arch lattice structure obtained by optimization is the arch height-to-span of 0.7, strut diameter of 1.2 mm and cell height of 4.5 mm. The corresponding elastic modulus is measured at 2.012 GPa, while the compressive strength reaches 79.254 MPa. These values represent a respective increase of 21.57% and 35.60% compared to the non-optimized configuration. The mechanical properties of the structure have been significantly enhanced. This research can provide references for the design and optimization of lightweight lattice structures.
- selective laser melting /
- structure parameters /
- arched lattice /
- elasticity modulus /
- compression strength
王庆龙

HTML全文

轻量化设计是航空航天、智能制造等领域结构设计的核心^[1],多孔结构材料因兼具结构和功能双重属性广泛应用于各领域,其中三维点阵作为杆件单元和节点按一定规律周期排列而成的有序多孔,具有高比强度、高比刚度、质轻等特点和良好的轻量化设计特性^[2-5],是结构轻量化的重要方式。

传统点阵结构制造方法如熔模铸造、金属丝编织和挤压线切割法等^[6-7],存在制造周期长、精度低以及复杂点阵成型困难等问题,极大地影响了点阵结构的工程应用^[8]。选区激光熔化技术(Selective laser melting, SLM)利用高能激光束熔化金属粉末逐层成型三维零件,因其设计自由度与成型精度高、制造周期短而常用于金属点阵的成型制造^[9-12]。近年来,许多学者采用选区激光熔化技术制备了各类胞元周期性分布的点阵结构,如四棱锥形、六面体、八面体、十二面体点阵结构等^{[1, 13-15]},并对点阵结构参数与力学性能之间的关系展开了一系列研究。

汪飞雪等^[1]在四棱锥点阵结构的研究中发现,结构的弹性模量随着径长比和杆件夹角的增大而增大。CRUPI等^[16]同样研究了不同径长比BCC点阵的压缩性能,得出点阵的弹性模量与抗压强度均对结构径长比存在正向依赖性。ZHU等^[17]为缓解节点应力集中进行新型余弦结构（CFBC）设计,发现杆径和周期长度对结构平台应力与能量吸收呈正相关趋势。同样地,纪小刚等^[18]基于仿生原理进行三维点阵设计,并展开不同单胞杆径下结构的压缩特性研究,发现单胞杆径的增大能提高结构的承载能力。而宋英杰等^[19]在点阵压缩断裂的研究中表明,节点是结构破坏的敏感位置,结构内径的增大使得第一最大压缩载荷不断减小。康建峰等^[20]采用有限元法对结构单元弹性模量进行研究,发现单元尺寸是调节多孔单元弹性性能的重要因素。MISHRA等^[21]探讨了晶格单元尺寸与壁厚对TPMS多孔结构压缩特性的影响,发现力学性能与单元尺寸和壁厚的函数关系,结构弹性模量与屈服强度随着单元尺寸的减小和壁厚的增大而显著提高。点阵结构参数与力学性能关系的研究表明,结构参数的改变使得点阵结构与内部孔隙发生了显著变化而影响了结构的力学性能。此外点阵结构中,整体力学性能是各结构参数共同作用下的结果。江尧峰等^[22]采用响应面法考虑了单胞杆长和倾斜角度等多结构参数交互作用,对SLM成型的316L体心立方点阵进行优化,提高了结构力学性能。然而,多数学者对点阵结构力学性能研究多集中于单因素改变,而对多参数间的交互影响研究较少,明确各种结构参数及其交互作用的影响规律,以更好地对点阵结构进行优化设计。

在结构轻量化设计时结构模量和强度是重要的力学参数^[9],本文以设计的拱形点阵为对象,基于SLM成型AlSi10Mg点阵结构,研究了拱形高跨比、单胞杆径、胞元高度3个结构参数及其交互作用对结构弹性模量与抗压强度的影响,通过结构参数优化提升了点阵结构的力学性能。本研究将拱形特征融入点阵结构,综合考虑了各结构参数及其交互影响对点阵结构力学性能的作用规律,可为轻量化点阵结构的设计与优化提供参考。

1 实验部分

1.1 点阵结构与方案设计

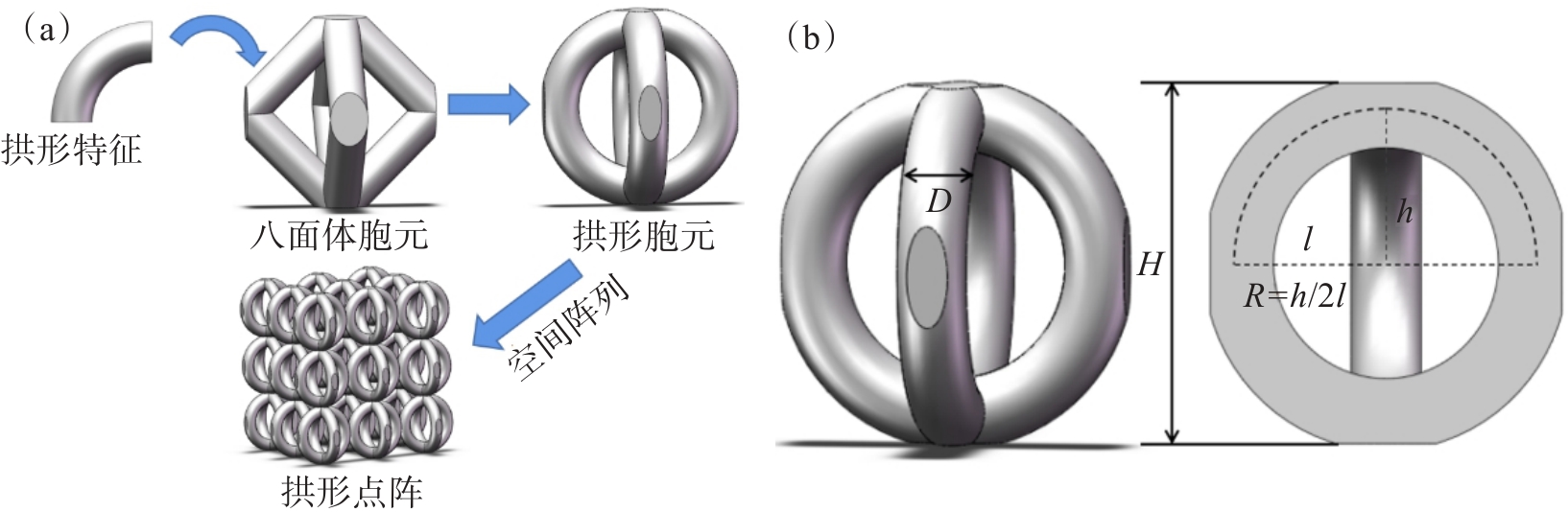
三维点阵由杆件单元和节点组成的胞元按一定规律周期性排列而成,作为可紧密连接填充空间并使得空间剩余体积最小的多面体,八面体胞元组成的结构可在空间内独立排布,在结构简单的同时还有优异的压缩性能^[23]。此外相比于梁柱直构件,拱形结构具有在承受竖向荷载作用下将产生的弯矩转化为轴向压力的显著受力特点,将拱形特征引入点阵单元可提高结构的稳定性与承载能力^[24-25]。本文将拱形特征和点阵结构相结合,在八面体胞元基础上融入拱形特征,利用三维建模软件建立拱形胞元模型,最终阵列形成拱形点阵,如图1（a）所示。

图 1 拱形点阵（a）与结构参数（b）设计

Figure 1. Arch lattice （a） and structural parameter （b） design

下载: 全尺寸图片幻灯片

点阵结构参数与力学性能关系的研究表明,结构参数的改变将影响点阵的力学性能。在拱形胞元设计后需明确点阵的具体结构参数,分析其对结构力学性能的影响规律。拱形高跨比（R）、单胞杆径（D）和胞元高度（H）为拱形点阵中3个重要的设计参数,其中拱形高跨比（R）指的是拱形中心线上拱高（h）与跨长（2l）的比值,单胞杆径（D）和胞元高度（H）分别为拱形胞元任一圆形截面上的径长和在压缩方向上的尺寸,如图1（b）所示,三者之间不同的组合将形成不同的拱形点阵结构。经前期相关研究,本文将对单胞杆径在0.8~1.2 mm、高跨比在0.3~0.7、胞元高度在4.5~5.5 mm之间的点阵结构进行优化研究。

响应面法（RSM）是通过建立统计模型来评估各因素之间的影响规律和交互作用,进而确定最优实验条件的一种综合试验设计和优化分析方法,具有试验次数少、预测精度高等优点^[26-28]。

本文采用Box-Behnken响应曲面法对结构参数进行三因素三水平的试验设计,其中输入因素分别为拱形高跨比（R）、单胞杆径（D）和胞元高度（H）,响应值为结构弹性模量（E）和抗压强度（P）。通过对各影响因子的编码使每个因子在高水平（+1）、中心点（0）、低水平（-1）上变化,整体共设17组试验,包括12个轴向试验和5个中心重复试验,试验因素水平和设计方案见表1、表2。

表 1 响应曲面的因素与水平

Table 1. Factors and levels of response surface

影响因素		水平
影响因素	-1	0	1
高跨比（R）	0.3	0.5	0.7
单胞杆径（D）/mm	0.8	1.0	1.2
胞元高度（H）/mm	4.5	5.0	5.5

下载: 导出CSV

| 显示表格

表 2 试验设计方案与结果

Table 2. Experimental design scheme and results

序号	R	D/mm	H/mm	E/GPa	P/MPa
1	0.5	0.8	4.5	0.442	10.872
2	0.5	1.0	5.0	0.535	15.712
3	0.5	1.0	5.0	0.505	16.505
4	0.3	1.2	5.0	0.297	7.735
5	0.5	1.0	5.0	0.531	15.810
6	0.5	1.0	5.0	0.550	16.677
7	0.7	0.8	5.0	0.643	18.570
8	0.5	1.0	5.0	0.581	16.691
9	0.5	1.2	4.5	1.251	41.864
10	0.3	1.0	5.5	0.122	3.482
11	0.7	1.0	4.5	1.482	51.582
12	0.7	1.2	5.0	1.655	58.449
13	0.7	1.0	5.5	0.985	25.037
14	0.5	1.2	5.5	0.756	21.863
15	0.3	1.0	4.5	0.226	5.617
16	0.3	0.8	5.0	0.071	2.502
17	0.5	0.8	5.5	0.201	4.667

下载: 导出CSV

| 显示表格

1.2 实验材料与结构成型

本次实验选用气雾化法制备的AlSi10Mg粉末材料为研究对象,粉末粒径分布在15~53 μm,图2（a）所示为粉末的SEM形貌,可看出AlSi10Mg粉末基本上呈规则的球形,部分粉末表面黏附卫星粉,粉末的化学成分见表3。使用前将粉末置于70 ℃烘干箱中烘干6 h以上。

图 2 AlSi10Mg粉末形貌（a）及拱形点阵成型（b）

Figure 2. Morphology of AlSi10Mg powder （a） and arched lattice formation （b）

下载: 全尺寸图片幻灯片

表 3 AlSi10Mg粉末的化学成分

Table 3. Chemical composition of AlSi10Mg powder

成分	Si	Mg	Zn	Fe	Mn	Ni	Cu	Al
含量	9.0~11.0	0.20~0.45	≤0.10	≤0.55	≤0.45	≤0.05	≤0.05	余量

下载: 导出CSV

| 显示表格

试验成型设备为德国SLM-Solution公司生产的SLM125-HL,选用的成型工艺参数如下：激光功率292 W,扫描速度1 095 mm/s,扫描间距0.1 mm,铺粉层厚30 μm。为避免成型过程中发生氧化反应,选用氩气作为保护气,成型前通过循环氩气使成形腔内的氧含量低于0.1%,再激光启动并按设定的轨迹于铝基板上打印样件,打印完成后通过电火花线切割从基板上切除样件,最后用超声去除样品表面附着粉末与油污。SLM成型的17组拱形点阵样件如图2（b）所示,可发现所成型点阵样件表面无明显的球化、裂纹、翘曲等缺陷,部分杆件周围存在少许金属粉末黏附现象,点阵结构整体成型良好。

采用DNS300电子万能试验机对点阵结构进行准静态压缩性能试验。试验机的压缩进给速度设为3 mm/min,采样频率为5 Hz。根据压缩试验得到点阵结构力-位移曲线,通过式（1）、式（2）将其转化为应力-应变曲线,从曲线中获得点阵结构弹性模量和抗压强度相关数值。

ε = Δ L / L

(1)

σ = F / A

(2)

式（1）、式（2）中： $Δ L$ 为压缩位移量, $L$ 为拱形点阵试样压缩方向的尺寸, $F$ 为万能试验机测得的压缩载荷, $A$ 为试样受压面积。

2 结果与讨论

2.1 拱形点阵压缩分析

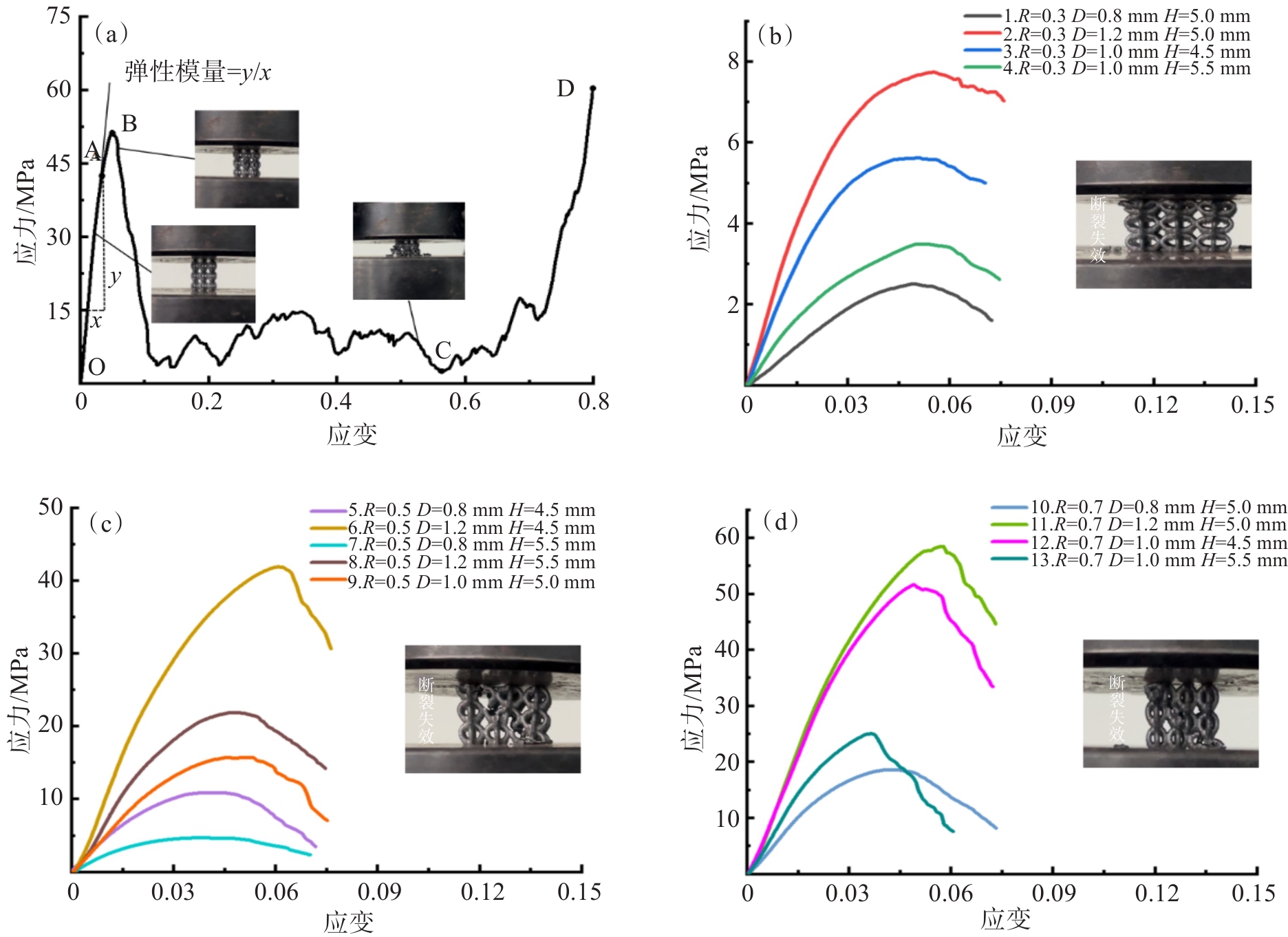
点阵压缩试验中发现结构的压缩过程主要可分为3个阶段：弹塑性阶段OB、应力波动阶段BC、致密压溃阶段CD,对应的应力-应变曲线如图3（a）所示。在压缩初始的OA阶段,压头开始对点阵结构缓慢施加载荷,此时压缩应力较小且保持线性增长,样件仅发生弹性变形。此后压缩应力不断增大,结构进入塑性变形阶段AB。随着压缩的进行,结构上应力持续增长,结构变形不断增大直至达到强度极限,此时点阵结构拱形杆间节点处发生断裂导致应力骤降,后应变的增加使曲线呈低应力状态并出现多处波动。最后进入致密压溃阶段CD,此时整体结构断裂失效,断裂杆件之间相互干涉,直到结构被整体压实。

图 3 拱形点阵应力-应变曲线：（a）拱形点阵压缩过程;（b）高跨比R=0.3压缩曲线;（c）高跨比R=0.5压缩曲线；（d）高跨比R=0.7压缩曲线

Figure 3. Arch lattice stress-strain curve: （a） Arch lattice compression process; （b） Height-to-span ratio R=0.3 compression curve; （c） Height-to-span ratio R=0.5 compression curve; （d） Height-to-span ratio R=0.7 compression curve

下载: 全尺寸图片幻灯片

通过分析压缩试验中获得拱形点阵弹性模量和抗压强度的相关数据,发现不同结构参数组合下点阵的力学性能存在较大的差异。当高跨比R=0.7、单胞杆径D=1.2 mm、胞元高度H=5.0 mm时,点阵结构的弹性模量和抗压强度同时达到最大值,分别为1.655 GPa和58.449 MPa,而最小的弹性模量和抗压强度仅为0.071 GPa和2.502 MPa,弹性模量最大相差1.584 GPa,抗压强度最大相差55.947 MPa。拱形点阵压缩应力-应变曲线如图3（b）、图3（c）、图3（d）,分析1、2,5、6,10、11组相关曲线结果发现,随着单胞杆径的增大,曲线断裂初始峰值应力和弹性阶段的斜率随之增大,点阵结构弹性模量与抗压强度均得到提高。而3、4,6、8,12、13组曲线表明不同高跨比下,胞元高度的增大均不利于获得高弹性模量和抗压强度的点阵样件。4、9、13组曲线反映了高跨比对结构力学性能的影响,从中发现高跨比为0.3的点阵样件整体的弹性模量与抗压强度较低,承载能力较弱。当高跨比R为0.3,单胞杆径D=1.0 mm,胞元高度H=5.5 mm时,结构弹性模量与抗压强度仅为0.122 GPa和3.482 MPa,而随着高跨比增大至0.7时,弹性模量和抗压强度分别为0.985 GPa和25.037 MPa,结构力学性能得到显著提高。

此外在压缩过程中,SLM成形的AlSi10Mg拱形点阵均表现出断裂失效,其断口SEM形貌如图4所示。图4中发现断口表面较为规则,在高倍镜下,断面主要由明显的阶梯式解理面组成,这是脆性状态下断裂面的一种独特形式,断裂区未发生明显的塑性变形,整体上主要表现出脆性断裂的特征。这与LI等^[29]在AlSi10Mg点阵结构压缩断裂研究中的结论一致。

图 4 点阵断口形貌：（a）断口形貌；（b）局部放大形貌

Figure 4. Fracture topography of lattice structure：（a） fracture morphology；（b） locally enlarged morphology

下载: 全尺寸图片幻灯片

2.2 响应面试验分析

2.2.1 响应模型建立与显著性分析

二阶回归模型作为描述自变量与因变量常见的数学模型,具有较强的灵活性与准确性。基于多项式回归模型理论,建立二阶多项式方程：

y = β_{0} + \sum_{i = 1}^{k} β_{i} x_{i} + \sum_{i = 1, j > i}^{k} β_{i j} x_{i} x_{j} + \sum_{i = 1}^{k} β_{i i} x_{i}^{2} + ε

(3)

式（3）中： $y$ 为响应值, $β_{0}$ 、 $β_{i}$ 、 $β_{i j}$ 、 $β_{i i}$ 为回归系数, $x_{i}$ 、 $x_{j}$ 为自变量, $ε$ 代表试验误差。

二阶多项式中3个求和项分别表示主效应、交互作用效应和二次效应,利用Design-Expert根据压缩试验数据进行多元回归分析,建立以拱形高跨比、单胞杆径、胞元高度为变量,弹性模量与抗压强度为响应量的二阶多项式响应面数学模型。

结构参数与弹性模量数学模型：

$E$ =0.540 4+0.506 1R+0.327 8D-0.164 6H+

0.1965RD-0.098 2RH-0.068 5DH+

0.086 2R²+0.039 9D²+0.077 2H²

(4)

结构参数与抗压强度数学模型：

$P$ =16.28+16.79R+11.66D-6.86H+8.66RD-

6.10RH-3.45DH+3.57R²+1.96D²+1.58H²

(5)

式（4）和式（5）中：E和P分别为结构弹性模量和抗压强度,R、D、H分别代表拱形高跨比、单胞杆径和胞元高度。

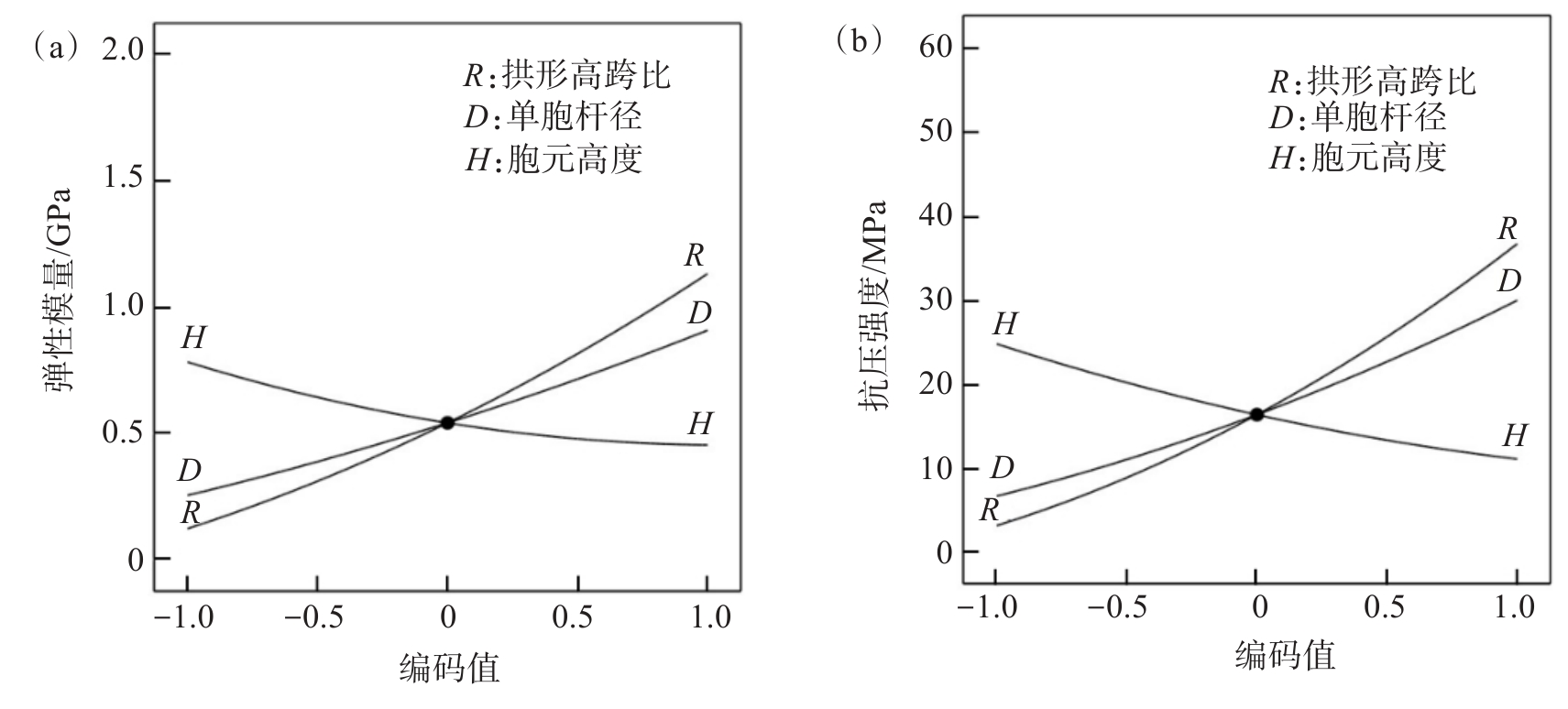
数学模型直接反映了各结构参数对点阵结构弹性模量和抗压强度的影响关系。其中结构参数系数的绝对值代表着该结构参数的影响程度大小,系数的正负反映了与响应值之间的正负相关性^[30]。可知结构参数范围内胞元高度、单胞杆径、拱形高跨比对结构弹性模量和抗压强度的影响程度依次增大,其中拱形高跨比和单胞杆径对结构弹性模量及抗压强度影响呈正相关性,胞元高度与结构弹性模量及抗压强度之间呈负相关性。

通过弹性模量与抗压强度的方差分析表4、表5可知,弹性模量和抗压强度模型的P-value值均小于0.000 1,而失拟项的P-value值分别为0.116 5和0.163 7均大于0.05,即模型检验显著,失拟项检验不显著,表明模型拟合精度高,可精确预测各结构参数对弹性模量和抗压强度之间的作用关系。2个模型的决定系数值R²分别为0.996 5与0.999 3,均接近1,Adj R²与Pred R²相近,表明试验值与预测值具有高度相关性。通过对结构弹性模量与抗压强度方差分析可知,响应模型准确度较高,各结构参数及其交互作用对结构弹性模量和抗压强度均有非常显著的影响。

表 4 弹性模量方差分析

Table 4. Analysis of elastic modulus variance

变量来源	平方和	自由度	均方	F-value	P-value	评价
模型	3.410 0	9	0.378 5	222.79	<0.000 1	显著
R	2.050 0	1	2.050 0	1 206.08	<0.000 1	显著
D	0.859 4	1	0.859 4	505.76	<0.000 1	显著
H	0.216 8	1	0.216 8	127.60	<0.000 1	显著
RD	0.154 4	1	0.154 4	90.90	<0.000 1	显著
RH	0.038 6	1	0.038 6	22.72	0.002 0	显著
DH	0.018 8	1	0.018 8	11.05	0.012 7	显著
残差	0.011 9	7	0.001 7	—	—	—
失拟项	0.008 8	3	0.002 9	3.76	0.116 5	不显著
R²=0.996 5 Adj R²=0.992 0 Pred R²=0.957 5
注：注“—”代表此项无数据。

注：注“—”代表此项无数据。

下载: 导出CSV

| 显示表格

表 5 抗压强度方差分析

Table 5. Analysis of compressive strength variance

变量来源	平方和	自由度	均方	F-value	P-value	评价
模型	4 304.25	9	478.25	1 140.02	<0.000 1	显著
R	2 254.63	1	2 254.63	5 374.45	<0.000 1	显著
D	1 088.11	1	1 088.11	2 593.78	<0.000 1	显著
H	376.56	1	376.56	897.62	<0.000 1	显著
RD	300.09	1	300.09	715.33	<0.000 1	显著
RH	148.96	1	148.96	355.09	<0.000 1	显著
DH	47.58	1	47.58	113.42	<0.000 1	显著
残差	2.94	7	0.42	—	—	—
失拟项	2.02	3	0.67	2.92	0.163 7	不显著
R²=0.999 3 Adj R²=0.998 4 Pred R²=0.992 2
注：注“—”代表此项无数据。

注：注“—”代表此项无数据。

下载: 导出CSV

| 显示表格

2.2.2 弹性模量与抗压强度分析

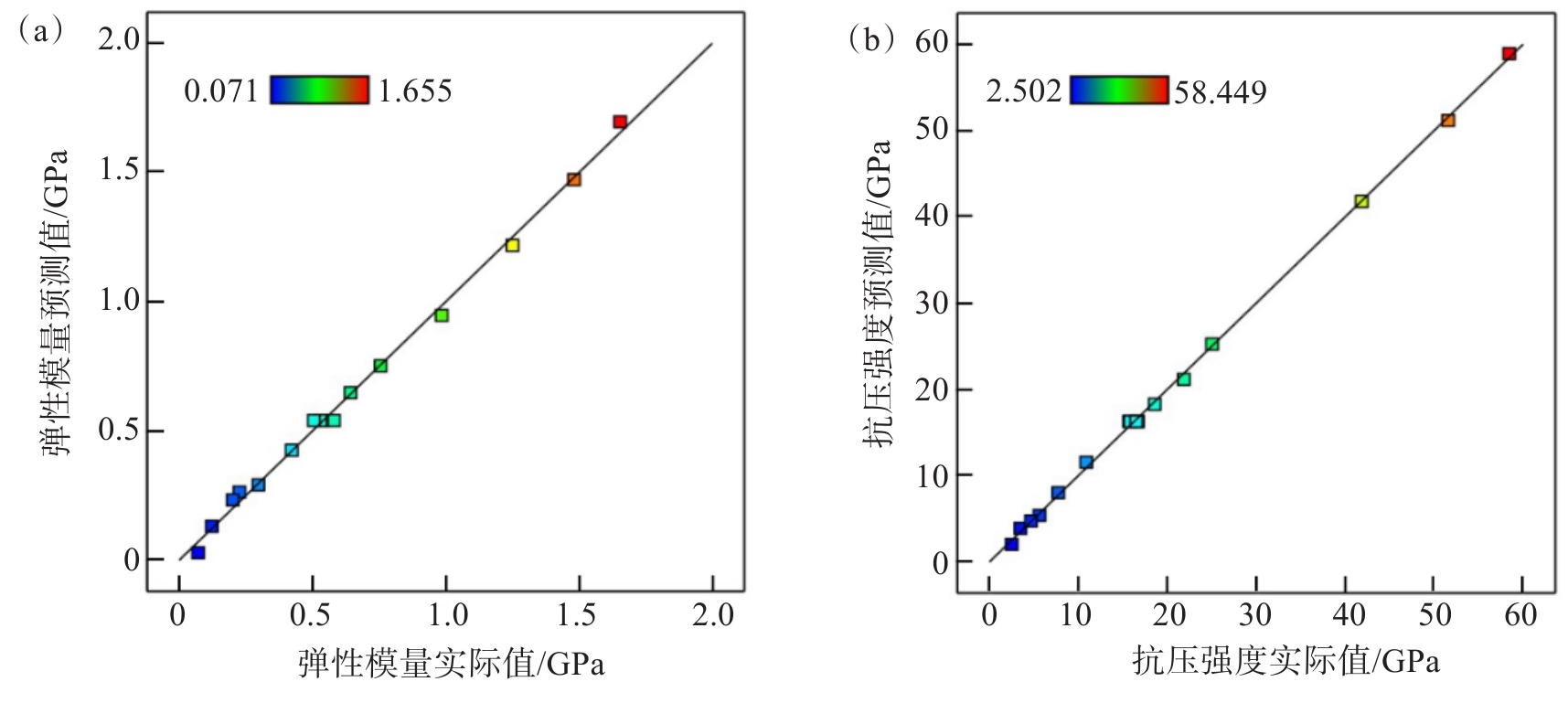
图5（a）、图5（b）所示分别为弹性模量和抗压强度的预测与实际值对应关系,图5中实际值基本位于y=z线性函数上,表明实验实际值与模型预测值误差小、预测精度高,模型能够较好地揭示点阵结构参数对弹性模量与抗压强度之间的作用关系。

图 5 弹性模量（a）与抗压强度（b）预测与实际值对应关系

Figure 5. Correspondence between predicted and actual values of elastic modulus （a） and compressive strength （b）

下载: 全尺寸图片幻灯片

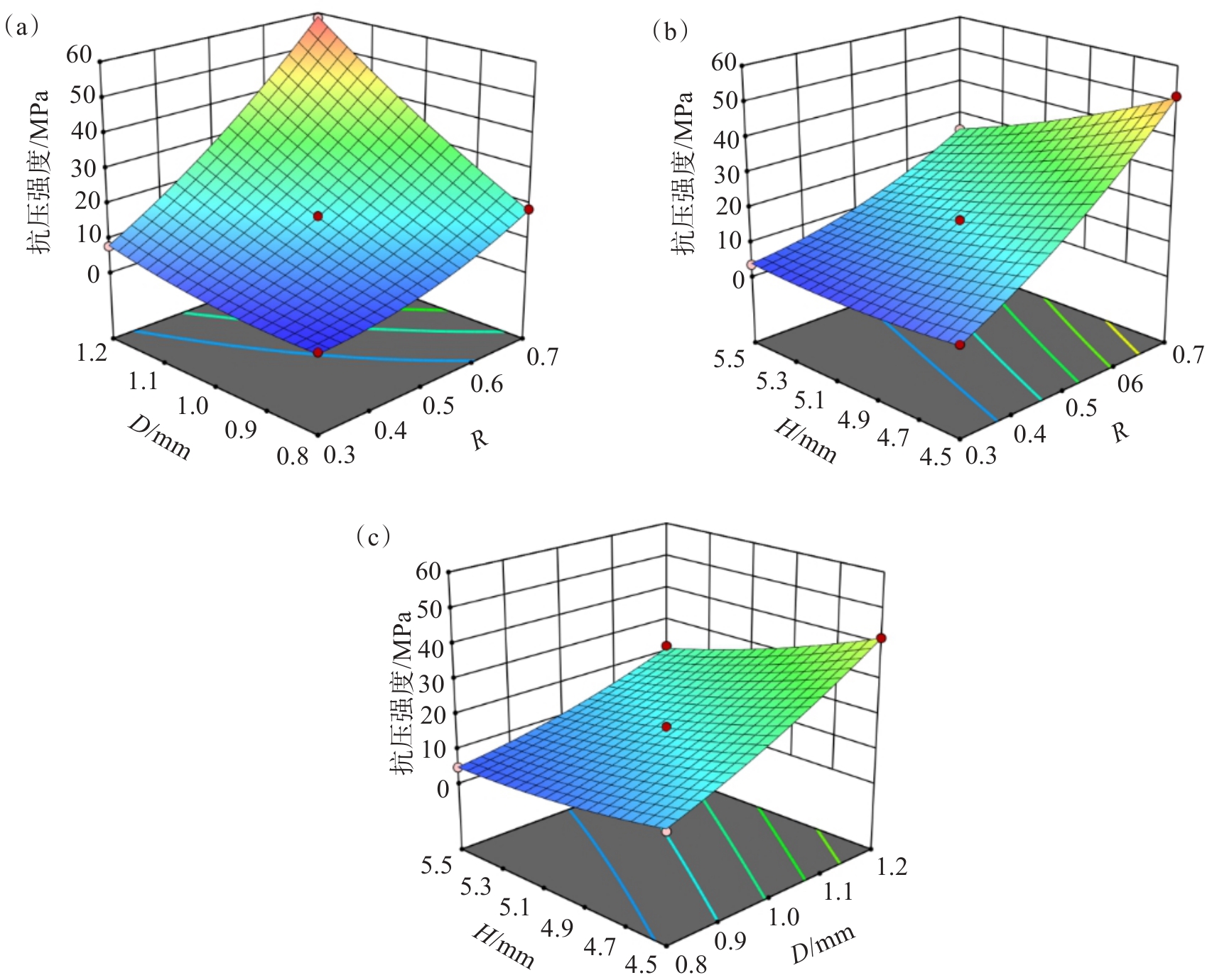
各结构参数对点阵弹性模量和抗压强度的影响规律如图6所示,分析发现各结构参数对点阵弹性模量和抗压强度均有显著的影响,且对点阵弹性模量和抗压强度的影响规律相似。其中弹性模量和抗压强度对拱形高跨比和单胞杆径具有正向依赖性。这是由于结构杆径增大时,杆件截面惯性矩大幅提高,增强了结构的抗变形能力,此外杆径的增大还对内部节点起到强化作用,因而随着杆径的增大,结构的弹性模量与抗压强度均有明显提高。而拱形高跨比主要影响了点阵胞元的形状,随着高跨比的增大,拱形结构拱高h与跨长2l的比值不断增大,使得结构的悬垂减小而提高了杆件的有效支撑体积,增强了压缩方向上结构的承载能力。作为调控结构尺寸与孔隙的重要参数,胞元高度与结构弹性模量和抗压强度呈负相关趋势,这主要是杆径与高跨比固定时胞元高度的增大将使得点阵结构整体尺寸与内部孔隙增大,导致点阵结构抵抗外部载荷的能力减弱,结构力学性能降低。其规律与应力-应变曲线中分析结果一致。

图 6 结构弹性模量（a）和抗压强度（b）影响规律

Figure 6. Influence of structural elastic modulus （a） and compressive strength （b）

下载: 全尺寸图片幻灯片

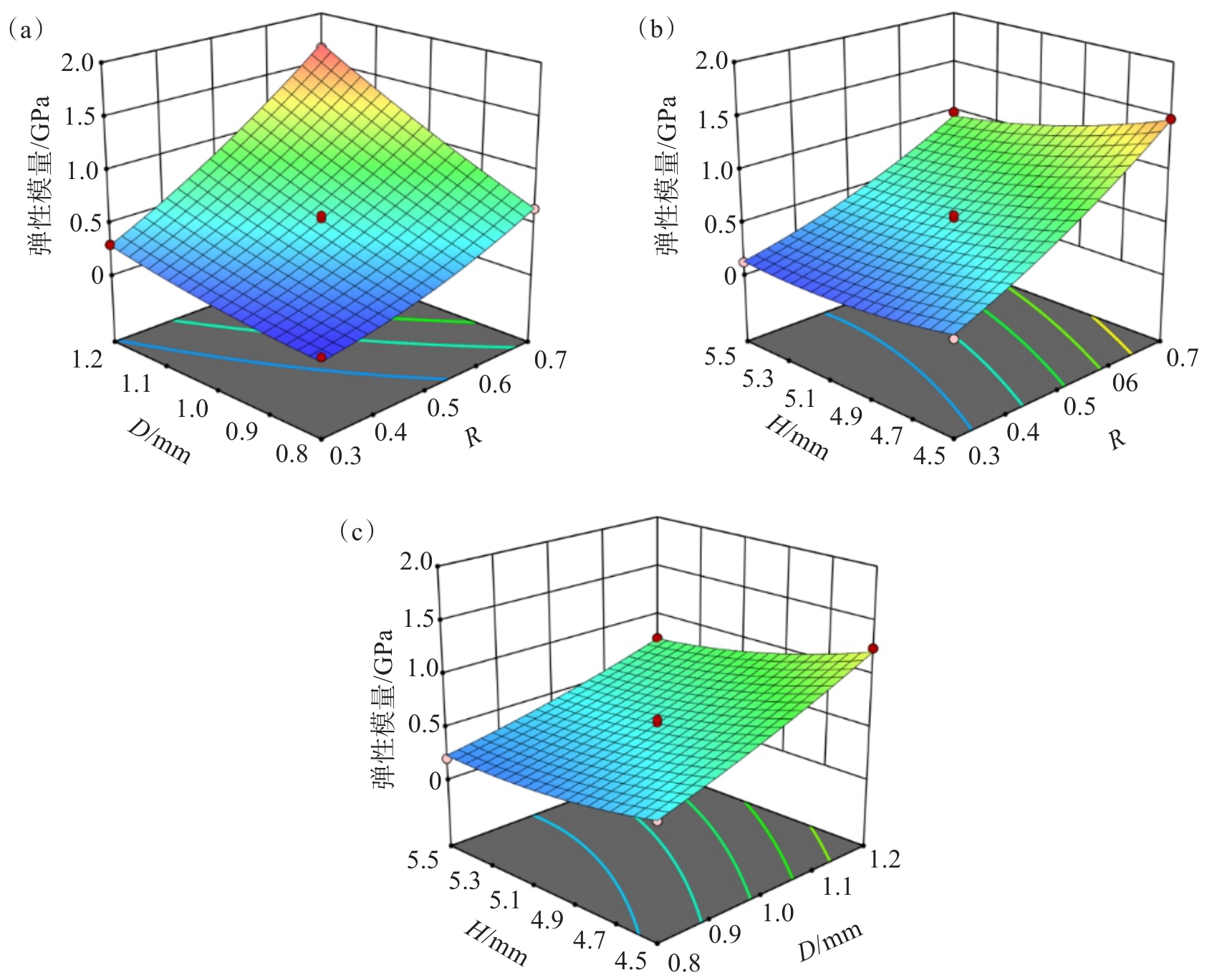
胞元高度为5.0 mm时RD交互作用对弹性模量与抗压强度的响应曲面如图7（a）、图8（a）所示,分析发现拱形高跨比与杆径的变化使得响应曲面起伏明显,随着拱形高跨比和杆径的同时增大,结构弹性模量与抗压强度迅速提高。这是由于高跨比的增大使得杆件水平悬垂减少,竖向支撑强度增大,同时结构杆径的增大强化了杆件变形抵抗能力,使得结构压缩方向的承载能力大幅提高。当杆径为1.2 mm、高跨比为0.7时,结构弹性模量与抗压强度达到最大值,分别为1.655 GPa和58.449 MPa,表明在较大的高跨比和杆径下,结构具备较强的承载能力。图7（b）、图8（b）反映了结构单胞杆径设置为1 mm时RH交互作用对结构弹性模量与抗压强度的影响,发现对于高跨比为0.3的点阵结构而言,胞元高度的变化使得结构弹性模量与压缩强度整体处于较低值,其弹性模量均小于0.5 GPa,抗压强度均小于10 MPa,结构压缩方向承载能力整体较弱,此时胞元高度变化对结构的弹性模量与抗压强度的影响不显著。而高跨比的增大使得结构压缩方向上支撑强度增大,结构承载能力显著提高,胞元高度变化对结构弹性模量与抗压强度的影响越为明显。图7（c）、图8（c）中拱形高跨比为0.5,此时随着胞元高度的增大,结构弹性模量和抗压强度总体呈下降趋势,而当单胞杆径增大时结构弹性模量与抗压强度增大,尤其是当胞元高度为4.5 mm时,随着杆径的增加,结构弹性模量与抗压强度显著增大。这主要是因为胞元高度较小时点阵整体的尺寸较小,而此时结构杆径的增大在增强变形抵抗能力的同时,对内部节点的强化作用较为明显,结构内部的承载能力得到明显提高。

图 7 弹性模量响应曲面:（a） RD交互响应面;（b） RH交互响应面;（c） DH交互响应面

Figure 7. Elastic modulus response surface graph: （a） RD interaction response surface; （b） RH interaction response surface; （c） DH interaction response surface

下载: 全尺寸图片幻灯片

图 8 抗压强度响应曲面:（a）RD交互响应面;（b）RH交互响应面;（c）DH交互响应面

Figure 8. Compressive strength response surface graph: （a） RD interaction response surface; （b） RH interaction response surface; （c） DH interaction response surface

下载: 全尺寸图片幻灯片

2.3 结构参数优化

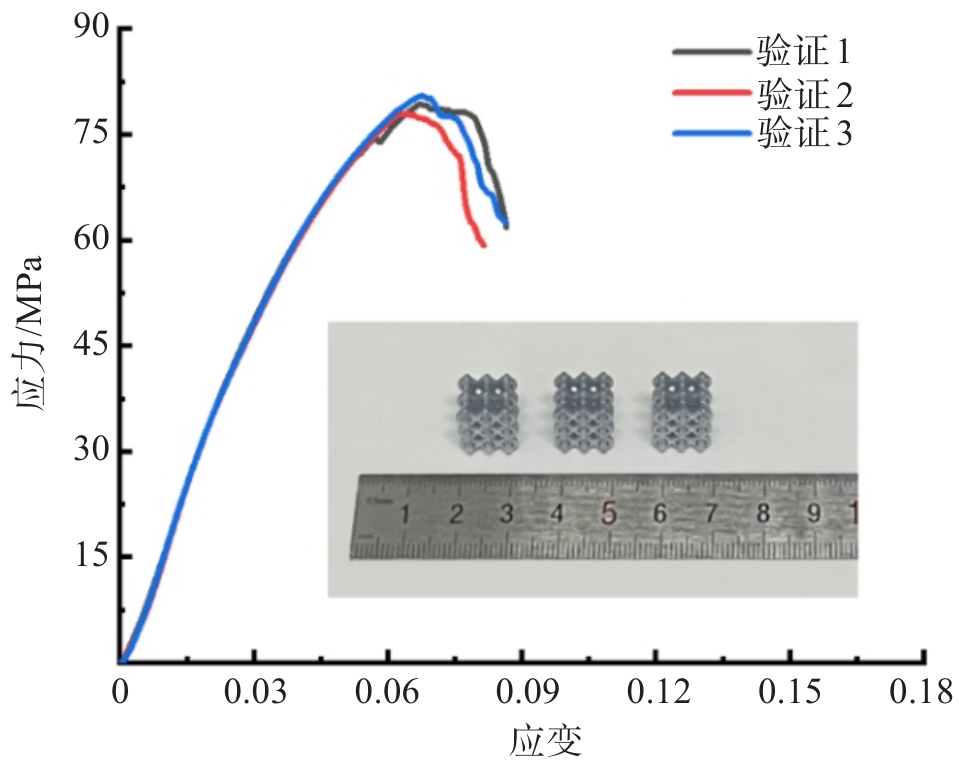
模量和强度是结构轻量化设计中的重要指标,为获得结构参数范围内弹性模量与抗压强度优异的参数组合,在响应面规律的基础上对结构参数进行优化分析与验证。本文以结构弹性模量与抗压强度最大为优化目标,设置如表6所列优化条件。得到期望最高的结构参数优化方案为拱形高跨比R=0.7、单胞杆径D=1.2 mm、胞元高度H=4.5 mm,在此参数下结构弹性模量与抗压强度的最大预测值分别为2.105 GPa和76.914 MPa,如表7所列。

表 6 优化条件及目标

Table 6. Optimization conditions and objectives

变量与响应	目标	限制		重要性
变量与响应	目标	下限	上限	重要性
拱形高跨比	范围内	0.3	0.7	3
单胞杆径/mm	范围内	0.8	1.2	3
胞元高度/mm	范围内	4.5	5.5	3
弹性模量/GPa	望大	0.071	2.5	5
抗压强度/MPa	望大	2.502	100	5

下载: 导出CSV

| 显示表格

表 7 预测与验证结果

Table 7. Prediction and verification results

序号	R	D/mm	H/mm	E/GPa	P/MPa
实验组	0.7	1.2	5.0	1.655	58.449
预测组	0.7	1.2	4.5	2.105	76.914
验证组	0.7	1.2	4.5	2.012	79.254

下载: 导出CSV

| 显示表格

根据预测的优化方案制备3组拱形点阵样件,通过准静态压缩试验获取应力-应变曲线,得到结构弹性模量与抗压强度,如图9所示。为减小实验误差取3组样件弹性模量与抗压强度平均值作为优化结果,得出优化后点阵样件弹性模量与抗压强度分别为2.012 GPa和79.254 MPa。相较于优化前样件,优化后结构样件弹性模量与抗压强度分别提升了21.57%与35.60%,这主要是由于当拱形点阵高跨比R=0.7、单胞杆径D=1.2 mm时,较小的结构悬垂与较强的变形抵抗能力使得结构压缩方向承载能力较高,在此条件下点阵胞元高度缩小至4.5 mm使得结构整体尺寸减小,在增大结构相对密度的同时强化了内部支撑结构,进一步提高结构承载能力。与预测值相比弹性模量与抗压强度的误差仅为4.42%和3.04%,表明建立的数学模型可精准对点阵结构力学性能进行优化预测。

图 9 验证组结构应力-应变曲线

Figure 9. Verify the stress-strain curve of the group structure

下载: 全尺寸图片幻灯片

3 结论

1）SLM成型的AlSi10Mg拱形点阵在压缩过程中发生断裂失效,断裂区未发生明显的塑性变形,整体表现为脆性断裂。

2）拱形高跨比对拱形点阵力学性能影响最为显著。在结构参数影响下,点阵弹性模量和抗压强度随着拱形高跨比和单胞杆径的增大而增大,随着胞元高度的增大而减小。结构杆径和高跨比处于较低水平时,点阵弹性模量与抗压强度受胞元高度变化的影响不显著,而高跨比和杆径的同时增大以及在增大高跨比的同时减小胞元高度可显著提高结构的力学性能。

3）响应面法优化得到拱形点阵的最优结构参数组合是高跨比为0.7、单胞杆径为1.2 mm、胞元高度为4.5 mm,在此条件下,其弹性模量为2.012 GPa、抗压强度为79.254 MPa,相较优化前结构弹性模量与抗压强度分别提升21.57%和35.60%。与预测值相比误差仅为4.42%和3.04%,预测精度高。表明建立的数学模型可精准对点阵结构力学性能进行优化预测,可为轻量化点阵的设计与优化提供参考。

王庆龙

图 1 拱形点阵（a）与结构参数（b）设计

Fig 1. Arch lattice （a） and structural parameter （b） design

下载: 全尺寸图片幻灯片

图 2 AlSi10Mg粉末形貌（a）及拱形点阵成型（b）

Fig 2. Morphology of AlSi10Mg powder （a） and arched lattice formation （b）

下载: 全尺寸图片幻灯片

图 3 拱形点阵应力-应变曲线：（a）拱形点阵压缩过程;（b）高跨比R=0.3压缩曲线;（c）高跨比R=0.5压缩曲线；（d）高跨比R=0.7压缩曲线

Fig 3. Arch lattice stress-strain curve: （a） Arch lattice compression process; （b） Height-to-span ratio R=0.3 compression curve; （c） Height-to-span ratio R=0.5 compression curve; （d） Height-to-span ratio R=0.7 compression curve

下载: 全尺寸图片幻灯片

图 4 点阵断口形貌：（a）断口形貌；（b）局部放大形貌

Fig 4. Fracture topography of lattice structure：（a） fracture morphology；（b） locally enlarged morphology

下载: 全尺寸图片幻灯片

图 5 弹性模量（a）与抗压强度（b）预测与实际值对应关系

Fig 5. Correspondence between predicted and actual values of elastic modulus （a） and compressive strength （b）

下载: 全尺寸图片幻灯片

图 6 结构弹性模量（a）和抗压强度（b）影响规律

Fig 6. Influence of structural elastic modulus （a） and compressive strength （b）

下载: 全尺寸图片幻灯片

图 7 弹性模量响应曲面:（a） RD交互响应面;（b） RH交互响应面;（c） DH交互响应面

Fig 7. Elastic modulus response surface graph: （a） RD interaction response surface; （b） RH interaction response surface; （c） DH interaction response surface

下载: 全尺寸图片幻灯片

图 8 抗压强度响应曲面:（a）RD交互响应面;（b）RH交互响应面;（c）DH交互响应面

Fig 8. Compressive strength response surface graph: （a） RD interaction response surface; （b） RH interaction response surface; （c） DH interaction response surface

下载: 全尺寸图片幻灯片

图 9 验证组结构应力-应变曲线

Fig 9. Verify the stress-strain curve of the group structure

下载: 全尺寸图片幻灯片

表 1 响应曲面的因素与水平

Table 1 Factors and levels of response surface

影响因素		水平
影响因素	-1	0	1
高跨比（R）	0.3	0.5	0.7
单胞杆径（D）/mm	0.8	1.0	1.2
胞元高度（H）/mm	4.5	5.0	5.5

下载: 导出CSV

表 2 试验设计方案与结果

Table 2 Experimental design scheme and results

序号	R	D/mm	H/mm	E/GPa	P/MPa
1	0.5	0.8	4.5	0.442	10.872
2	0.5	1.0	5.0	0.535	15.712
3	0.5	1.0	5.0	0.505	16.505
4	0.3	1.2	5.0	0.297	7.735
5	0.5	1.0	5.0	0.531	15.810
6	0.5	1.0	5.0	0.550	16.677
7	0.7	0.8	5.0	0.643	18.570
8	0.5	1.0	5.0	0.581	16.691
9	0.5	1.2	4.5	1.251	41.864
10	0.3	1.0	5.5	0.122	3.482
11	0.7	1.0	4.5	1.482	51.582
12	0.7	1.2	5.0	1.655	58.449
13	0.7	1.0	5.5	0.985	25.037
14	0.5	1.2	5.5	0.756	21.863
15	0.3	1.0	4.5	0.226	5.617
16	0.3	0.8	5.0	0.071	2.502
17	0.5	0.8	5.5	0.201	4.667

下载: 导出CSV

表 3 AlSi10Mg粉末的化学成分

Table 3 Chemical composition of AlSi10Mg powder

成分	Si	Mg	Zn	Fe	Mn	Ni	Cu	Al
含量	9.0~11.0	0.20~0.45	≤0.10	≤0.55	≤0.45	≤0.05	≤0.05	余量

下载: 导出CSV

表 4 弹性模量方差分析

Table 4 Analysis of elastic modulus variance

变量来源	平方和	自由度	均方	F-value	P-value	评价
模型	3.410 0	9	0.378 5	222.79	<0.000 1	显著
R	2.050 0	1	2.050 0	1 206.08	<0.000 1	显著
D	0.859 4	1	0.859 4	505.76	<0.000 1	显著
H	0.216 8	1	0.216 8	127.60	<0.000 1	显著
RD	0.154 4	1	0.154 4	90.90	<0.000 1	显著
RH	0.038 6	1	0.038 6	22.72	0.002 0	显著
DH	0.018 8	1	0.018 8	11.05	0.012 7	显著
残差	0.011 9	7	0.001 7	—	—	—
失拟项	0.008 8	3	0.002 9	3.76	0.116 5	不显著
R²=0.996 5 Adj R²=0.992 0 Pred R²=0.957 5
注：注“—”代表此项无数据。

注：注“—”代表此项无数据。

下载: 导出CSV

表 5 抗压强度方差分析

Table 5 Analysis of compressive strength variance

变量来源	平方和	自由度	均方	F-value	P-value	评价
模型	4 304.25	9	478.25	1 140.02	<0.000 1	显著
R	2 254.63	1	2 254.63	5 374.45	<0.000 1	显著
D	1 088.11	1	1 088.11	2 593.78	<0.000 1	显著
H	376.56	1	376.56	897.62	<0.000 1	显著
RD	300.09	1	300.09	715.33	<0.000 1	显著
RH	148.96	1	148.96	355.09	<0.000 1	显著
DH	47.58	1	47.58	113.42	<0.000 1	显著
残差	2.94	7	0.42	—	—	—
失拟项	2.02	3	0.67	2.92	0.163 7	不显著
R²=0.999 3 Adj R²=0.998 4 Pred R²=0.992 2
注：注“—”代表此项无数据。

注：注“—”代表此项无数据。

下载: 导出CSV

表 6 优化条件及目标

Table 6 Optimization conditions and objectives

变量与响应	目标	限制		重要性
变量与响应	目标	下限	上限	重要性
拱形高跨比	范围内	0.3	0.7	3
单胞杆径/mm	范围内	0.8	1.2	3
胞元高度/mm	范围内	4.5	5.5	3
弹性模量/GPa	望大	0.071	2.5	5
抗压强度/MPa	望大	2.502	100	5

下载: 导出CSV

表 7 预测与验证结果

Table 7 Prediction and verification results

序号	R	D/mm	H/mm	E/GPa	P/MPa
实验组	0.7	1.2	5.0	1.655	58.449
预测组	0.7	1.2	4.5	2.105	76.914
验证组	0.7	1.2	4.5	2.012	79.254

下载: 导出CSV

参考文献(30)

[1]	汪飞雪, 张天翊, 刘鹏举, 等. 基于SLM工艺的316L四棱锥点阵结构力学性能[J]. 塑性工程学报, 2021, 28(10): 99-106.
[2]	汤永锋, 路平, 刘斌, 等. 不同梯度变化方式的不规则多孔结构设计与力学性能分析[J]. 中国机械工程, 2022, 33(23): 2859-2866.
[3]	杨建明, 汤阳, 顾海, 等. 3D打印制备多孔结构的研究与应用现状[J]. 材料导报, 2018, 32(15): 2672-2682.
[4]	XIAO Z F, YANG Y Q, XIAO R, et al. Evaluation of topology-optimized lattice structures manufactured via selective laser melting[J]. Materials & Design, 2018, 143: 27-37.
[5]	杜义贤, 李涵钊, 田启华, 等. 基于能量均匀化的高剪切强度周期性点阵结构拓扑优化[J]. 机械工程学报, 2017, 53(18): 152-160.
[6]	赵冰, 李志强, 侯红亮, 等. 金属三维点阵结构制备技术研究进展[J]. 稀有金属材料与工程, 2016, 45(8): 2189-2200.
[7]	郑敏, 杨瑾, 张华. 多孔金属材料的制备及应用研究进展[J]. 材料导报, 2022, 36(18): 78-93.
[8]	吴鸿飞, 王维荣, 王国伟, 等. 选区激光熔化成形点阵结构的各向异性对力学性能的影响[J]. 稀有金属材料与工程, 2022, 51(4): 1397-1405.
[9]	任会兰, 申海艇, 栗建桥. 单轴压缩下Ti-6Al-4V空心点阵结构的力学行为[J]. 中国科学:技术科学, 2021, 51(3): 293-304.
[10]	曾寿金, 李传生, 刘广, 等. 选区激光熔化梯度多孔支架力学性能和能量吸收研究[J]. 中国机械工程, 2022, 33(19): 2364-2371.
[11]	PIRINU A, PRIMO T, DEL PRETE A, et al. Mechanical behaviour of AlSi10Mg lattice structures manufactured by the Selective Laser Melting (SLM)[J]. The International Journal of Advanced Manufacturing Technology, 2023, 124(5): 1651-1680.
[12]	谢芳浩, 李加南, 邓声华, 等. 选区激光熔化Al-Zn-Mg-Sc合金组织与性能研究[J]. 有色金属科学与工程, 2022, 13(4): 61-69, 147.
[13]	张国庆, 杨永强, 宋长辉, 等. 激光选区熔化成型CoCrMo多孔结构的设计与性能研究[J]. 中国激光, 2015, 42(11): 59-68.
[14]	SUN J F, YANG Y Q, WANG D. Mechanical properties of a Ti6Al4V porous structure produced by selective laser melting[J]. Materials & Design, 2013, 49: 545-552.
[15]	CAO X F, DUAN S Y, LIANG J, et al. Mechanical properties of an improved 3D-printed rhombic dodecahedron stainless steel lattice structure of variable cross section[J]. International Journal of Mechanical Sciences, 2018, 145: 53-63.
[16]	CRUPI V, KARA E, EPASTO G, et al. Static behavior of lattice structures produced via direct metal laser sintering technology[J]. Materials & Design, 2017, 135: 246-256.
[17]	ZHU G H, WEN D W, WEI L L, et al. Mechanical performances of novel cosine function cell-based metallic lattice structures under quasi-static compressive loading[J]. Composite Structures, 2023, 314: 116962.
[18]	纪小刚, 张建安, 栾宇豪, 等. 仿皮肤三维多孔点阵结构压缩吸能性能研究[J]. 机械工程学报, 2021, 57(15): 222-230.
[19]	宋英杰, 张红梅, 顾冬冬, 等. 激光增材制造NiTi轻量化点阵结构变形与回复行为[J]. 中国激光, 2022, 49(14): 231-243.
[20]	康建峰, 王玲, 孙畅宁, 等. 面向3D打印可变模量金属假体的微结构设计[J]. 机械工程学报, 2017, 53(5): 175-180.
[21]	MISHRA A K, CHAVAN H, KUMAR A. Effect of cell size and wall thickness on the compression performance of triply periodic minimal surface based AlSi10Mg lattice structures[J]. Thin-Walled Structures, 2023, 193: 111214.
[22]	江尧峰, 许明三, 曾寿金, 等. SLM成型316L体心立方点阵结构力学性能优化[J]. 塑性工程学报, 2023, 30(4): 178-186.
[23]	宋昊政. 基于SLM多孔结构腰椎融合器的设计与性能研究[D].杭州：杭州电子科技大学, 2020.
[24]	YAO J, ZHAO L, DING R C, et al. Study on the quasistatic compression performance of arch microstrut lattice structure by selective laser melting[J]. Advanced Engineering Materials, 2022, 24(5): 2101156.
[25]	ZHANG Y T, AIYITI W, DU S, et al. Design and mechanical behaviours of a novel tantalum lattice structure fabricated by SLM[J]. Virtual and Physical Prototyping, 2023, 18(1): 2192702.
[26]	王刚, 王馨, 宋小三, 等. 响应曲面法中BBD和CCD在优化巯基乙酰化壳聚糖制备条件中的比较[J]. 环境工程学报, 2018, 12(9): 2502-2511.
[27]	邢雷, 李金煜, 赵立新, 等. 基于响应面法的井下旋流分离器结构优化[J]. 中国机械工程, 2021, 32(15): 1818-1826.
[28]	周志伟, 龚红英, 贾星鹏, 等. 铝合金蓄能器壳体冷挤压成形多目标优化[J]. 有色金属科学与工程, 2021, 12(1): 67-74.
[29]	LI D M, QIN R X, XU J X, et al. Effect of heat treatment on AlSi10Mg lattice structure manufactured by selective laser melting: Microstructure evolution and compression properties[J]. Materials Characterization, 2022, 187: 111882.
[30]	段伟, 赵哲, 吉红伟, 等. 粉体性能及选区激光熔化打印工艺对AlSi10Mg合金致密化行为的影响[J]. 材料导报, 2019, 33(10): 1685-1690.

施引文献

资源附件(0)

图(9) / 表(7)

计量

文章访问数: 11
HTML全文浏览量: 1
PDF下载量: 1
被引次数: 0

1 实验部分
1.1 点阵结构与方案设计
1.2 实验材料与结构成型
2 结果与讨论
2.1 拱形点阵压缩分析
2.2 响应面试验分析
2.2.1 响应模型建立与显著性分析
2.2.2 弹性模量与抗压强度分析
2.3 结构参数优化
3 结论

选区激光熔化拱形点阵力学性能影响及优化

通讯作者: 许明三（1974— ）,教授,主要从事激光增材制造、硬脆材料加工技术研究。E-mail：xums368@163.com

计量

出版历程