二次铝灰烧结制备镁铝尖晶石材料

张勇; 何小娟; 喻成龙; 鲁美娟; 罗运阔; 方汉孙; 黄华军; 郭新春

doi:10.13264/j.cnki.ysjskx.2021.06.006

二次铝灰烧结制备镁铝尖晶石材料

江西农业大学国土资源与环境学院，南昌 330045

基金项目:

国家自然科学基金资助项目 52004113

详细信息

通讯作者:
张勇（1989—），男，博士，讲师，主要从事固体废物资源化利用方面的研究。E-mail：752607795@qq.com

中图分类号: TF09
计量
- 文章访问数: 164
- HTML全文浏览量: 73
- PDF下载量: 12
出版历程
- 收稿日期: 2021-06-04
- 发布日期: 2021-12-30
- 刊出日期: 2021-12-30

Sintering fabrication of magnesia-alumina spinel by secondary aluminum dross

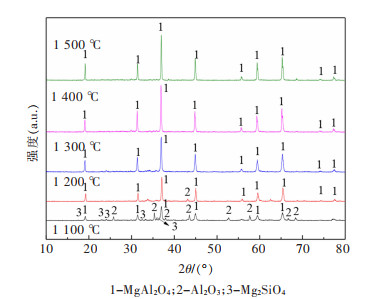
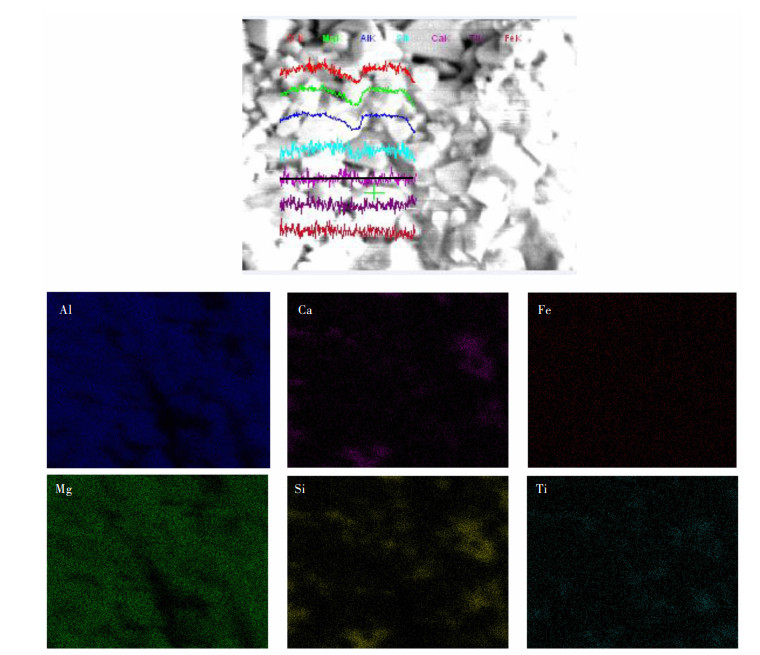
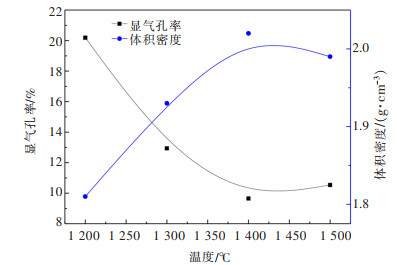
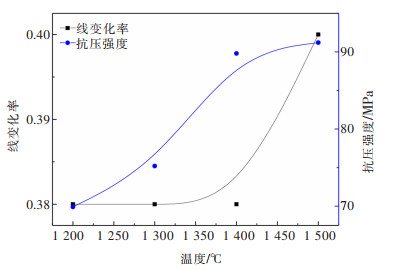
School of Land Resources and Environment, Jiangxi Agricultural University, Nanchang 330045, China

摘要

摘要: 以再生铝行业二次铝灰为主要原料，开展二次铝灰烧结制备镁铝尖晶石（MA）材料的研究。热力学分析表明，二次铝灰添加MgO，理论上可以制备出MA材料。研究结果表明，当二次铝灰和氧化镁质量分数比为1∶0.2，在1 100~1 500 ℃范围内，均能制备出MA材料；随烧结温度升高，MA材料纯度和结晶度明显提高，抗压强度呈升高趋势，显气孔率呈下降趋势。当烧结温度为1 400 ℃时，所制备出MA材料显气孔率和体积密度分别为9.65%和2.02 g/cm³，线变化率和抗压强度分别为38%和89.8 MPa，材料抗压强度达到国家行业标准《镁砖和镁铝砖》（GB/T 2275-2007）（40 MPa），即抗压强度≥40 MPa标准。上述结果表明，在二次铝灰中添加适量氧化镁，可以将二次铝灰烧结制备成镁铝尖晶石材料，实现资源化利用。
- 二次铝灰 /
- 烧结 /
- 镁铝尖晶石 /
- 性能
Abstract: Magnesia-alumina (MA) spinel by sintering secondary alumina ash from the secondary aluminum dross was studied. Thermodynamic analysis showed that MA material can be prepared theoretically by adding MgO to secondary aluminum ash. The results showed that MA spinel could be obtained under the sintering temperature from 1100 to 1500 ℃ when the mass ratio of aluminum dross to MgO was 1∶0.2, respectively. The purity and crystallinity of MA spinel improved significantly. In addition, the compressive strength increased, while apparent porosity decreased with the increasing of sintering temperature. When the sintering temperature was 1400 ℃, the apparent porosity and density of the prepared MA spinel were 9.65% and 2.02 g/cm³. The linear expansivity and the compressive strength were 38% and 89.8 MPa. The compressive strength of MA spinel reached the national standard of People's Republic of China for Magnesium brick and magnesium-aluminum brick (GB/T 2275-2007) (40 MPa), that is, the compressive strength was more than 40 MPa. The results showed that the MA spinel could be synthesis using the secondary aluminum dross with MgO. Therefore this technique provided the possibility of reutilization of the secondary aluminum dross in an environmentally friendly way.
- secondary aluminum dross /
- sintering /
- MA spinel /
- property

HTML全文

原地浸出工艺在我国南方离子型稀土矿中推广应用已有二十多年的历史^[1],工艺的不足逐渐显现,主要体现在2个方面：一是资源问题,表现在资源综合回收率偏低,据不完全统计,半数以上企业的资源综合回收率达不到75%^[2-3]；二是环境问题,表现在地质灾害频发,如江西龙南离子型稀土矿山因原地浸矿发生规模小、数量多的滑坡等地质灾害^[4]。不同矿山具有不同的开采技术条件,需要进行专门的浸渗环节设计,但目前国内矿山生产管理粗放,常常简单套用一成不变的方法,甚至生搬硬套其他矿山的工艺和参数^[5-6],是产生上述问题的主要原因。

研究表明,上述“资源-环境”问题均主要与矿山“注液-收液”的浸渗过程密切相关。浸渗过程的资源损失主要有浸矿盲区、母液渗漏和反吸附3部分^[7],其中,前２项损失主要是注液工程、收液工程布置不合理及注液强度不当引起的。浸矿液流经矿体会对矿体的抗剪强度产生弱化作用^[8-9],尤其是当注液强度大于矿山的出渗能力时,矿山浸润面不断上升,当浸润面达到临界水位面以上时,即可在瞬间发生滑坡^[10]。而浸润面的高低形状则取决于矿山的水文地质条件、渗透性能、注液强度与出渗能力等因素。

对“浸渗环节”,很多学者基于室内试验,在机理层面研究了浸矿过程的浸出动力学^[11-13]与传质过程^[14-17],以筛选浸矿剂^[18-20]、优化浸矿工艺；部分学者基于矿山生产现场试验,研究了原地浸矿过程中矿山内浸润面、土水压力及边坡表面裂缝的变化规律^[4,21],提出矿山滑坡的防控措施^[22]。这些研究成果为浸渗环节“事中观测,事后总结”阶段提供了有力的帮助,但难以用于“事先预测（设计）”阶段。因此,池汝安等^[23]指出,从矿山宏观水动力学角度研究浸取剂溶液在矿体内部的渗流规律,可以更好地指导离子型稀土矿的原地浸出。

本文选取浑圆形裸脚式稀土矿山为研究对象,建立原地浸矿“注液-收液”轴对称简化模型,基于地下水动力学和Dupuit假定,在已知矿山地形条件及注液条件下推导矿山稳定浸润线方程,为原地浸矿浸渗环节的“事先预测（设计）”提供理论依据。

1 浑圆形裸脚式矿山原地浸矿稳定浸润线理论分析

1.1 矿山“注液-收液”轴对称简化模型

我国南方离子型稀土矿区多为低山丘陵地形,山头多为不规则的浑圆形^[24]。离子型稀土矿原地浸出工艺注液工程一般为梅花形布置的注液孔,沿山顶往山腰的一定范围内布置,注液孔直径一般为Φ=0.15～0.30 m,深度一般为见矿0.5～1.0 m。收液工程则根据矿山具体的工程地质条件确定,其中,裸脚式矿山具有较完整的天然基岩底板,且在山脚或山谷处有基岩出露,常在山脚开挖集液沟收集母液^[25],其工艺如图1所示,图2所示为江西某浑圆形稀土矿山照片。

图 1 裸脚式稀土矿山原地浸出工艺示意

Figure 1. Schematic diagram of the in-situ leaching process of a bare-foot rare earth mine

下载: 全尺寸图片幻灯片

图 2 江西某浑圆形稀土矿山

Figure 2. A rounded rare earth mine in Jiangxi Province

下载: 全尺寸图片幻灯片

对于浑圆形裸脚式矿山,沿过中心轴线截取剖面,可得到“注液-收液”轴对称简化模型,如图3所示,对该模型作如下主要假设：

图 3 浑圆形裸脚式矿山“注液-收液”轴对称简化模型

Figure 3. The “liquid injection- liquid collection” simplified axisymmetric model of a rounded barefoot type mine

下载: 全尺寸图片幻灯片

1）假设地表径流与地下径流分水岭在平面上重合处可作为中心轴线（r = 0）,过中心轴线作垂直的H轴,取水平r轴与集液沟底板山脚出露点（图3中点C,坐标为r₃,单位为m）相交,建立坐标系。

2）原地浸矿工艺要求集液沟能及时排除出渗母液,因此,可取点C为水头基准点（H_c= 0）。

3）基岩底板坡度一般较小,地形一般会有起伏,模型中简化为直线坡,按平均值β取值（单位：（°））。

4）修建集液沟时会挖除坡脚表层黏土直至矿层（见图1）,因此,山坡出渗点B（坐标为r₂,单位为m）处的坡度α（单位（°））一般较大。

5）图3中地下水的运动分为2个部分：①浸润线之上的注液区为非饱和渗流,属于土壤水分运动范畴,此处水流主要为在重力作用下的垂直向下渗流。单孔注液时,溶液从注液孔往周围非饱和矿体入渗,距离孔越远,矿体饱和度越低,湿润体的形状类似为椭球体^[26-28]；孔网注液时,由于孔与孔之间的相互影响,使得溶液在孔底以下一定范围外的非饱和矿体中的入渗变得均匀^[25]。因此,图3中注液区（注液范围为r₁,单位为m）的边界条件简化为均匀的入渗强度W（单位水平面积、单位时间内入渗补给到地下水的水量,单位为m/d）。②浸润线之下基岩底板之上的区域为饱和渗流,属于地下水动力学范畴,此处水流主要为在重力、基岩坡度及液面比降作用下的水平流动。本文浸润线方程主要由第二部分水流在地下水动力学原理下进行推导,因此,当基岩底板坡度比较平缓、液面比降不太大的情况下,可以忽略垂向分流速而采用Dupuit假定。

6）随着注液的持续进行,矿体内部逐渐从基岩底板开始往上饱和,浸润线也越来越高,直至趋于稳定。一般情况下,原地浸矿生产周期6~8个月,浸矿剂溶液在前40天左右注完^[4],而后注入上清液,此时矿体内的浸润线已接近于稳定浸润线（图3中虚线所示）。因此,可以用稳定浸润线近似代替实际最高浸润线。

7）本文不考虑矿山土体渗透系数的空间变异性及各向同性。

1.2 稳定浸润线方程的推导

将图3视为轴对称问题,即假设在环向没有水流,过水断面为以点O为圆心的圆柱面,水头线为上凸的曲线。分析图3的流线可知,水流有径向和垂向2个方向的分流速,属于轴对称二维流。若允许引进Dupuit假定,忽略垂向分流速,则水流可简化为径向的一维流动计算^[29]。

对于裸脚式稀土矿山,基岩底板一般从分水岭向集液坑方向（流线方向）呈顺坡倾斜（本文不考虑角度的正负值,取图3中α＞β＞0 °）,当β＜20 °时,渗流长度可以用径向距离来近似表示^[29],水力坡度表示为-dH/dr。此时,H（r）=h（r）+tanβ·（r₃-r）,dH/dr= dh/dr-tanβ。依据水均衡原理,利用分段法,可得任意渗流断面处的总流量公式为：

Q (r) = \{\begin{array}{l} W π r^{2} 0 \leq r \leq r_{1} \\ W π r_{1}^{2} r_{1} \leq r \leq r_{2} \end{array}

(1)

式（1）中：Q（r）为任意渗流断面处的总流量数值,单位m³/d；W为注液入渗强度数值,单位m/d；r为任意渗流断面径向坐标数值,单位m；r₁为注液范围数值,单位m；r₂为出渗点B坐标数值,单位m。

根据Dupuit微分方程

\begin{array}{l} Q (r) = 2 π r h \cdot (- k_{s} \frac{d H}{d r}) = \\ - 2 π r k_{s} [H - t a n β \cdot (r_{3} - r)] \frac{d H}{d r} \end{array}

(2)

式（2）中：β为基岩坡度数值,单位（°）。

对于注液区域（0≤r≤r₁）,可得

- 2 π r k_{s} [H - t a n β \cdot (r_{3} - r)] \frac{d H}{d r} = W π r^{2}

(3)

分离变量后,令λ = W/k_s,作0→r的不定积分

\int_{H_{0}}^{H} H d H - t a n β \cdot r_{3} \int_{H_{0}}^{H} d H + t a n β \cdot \int_{H_{0}}^{H} r d H = - \frac{λ}{2} \int_{0}^{r} r d r

(4)

由于H与r之间的函数关系未知,式（4）左边第三项无法积分,但可根据积分中值定理近似求解。令 $\int_{H_{0}}^{H} r d H = r_{m} (H - H_{0})$ ,r_m介于0→r之间,由于浸润线方程光滑,可近似取r_m= r/2。因此,得到倾斜底板注液区域（0≤r≤r₁）稳定浸润线方程

H^{2} - t a n β \cdot (H - H_{0}) \cdot (2 r_{3} - r) + \frac{λ}{2} r^{2} = H_{0}^{2} 0 \leq r \leq r_{1}

(5)

对于非注液区域（r₁≤r≤r₂）,可得

- 2 π r K_{s} [H - t a n β \cdot (r_{3} - r)] \frac{d H}{d r} = W π r_{1}^{2}

(6)

分离变量后,作r₁→r的不定积分

\int_{H_{1}}^{H} H d H - t a n β \cdot r_{3} \int_{H_{1}}^{H} d H + t a n β \cdot \int_{H_{1}}^{H} r d H = - \frac{λ r_{1}^{2}}{2} \int_{r_{1}}^{r} \frac{d r}{r}

(7)

同理,根据积分中值定理近似求解式（7）左边第三项。令 $\int_{H_{1}}^{H} r d H = r_{d} (H - H_{1})$ ,r_d介于r₁→r之间,由于浸润线方程光滑,可近似取r_d=（r₁+r）/2。因此,得到倾斜底板非注液区域（r₁≤r≤r₂）稳定浸润线方程

\begin{array}{l} H^{2} - t a n β \cdot (H - H_{1}) \cdot (2 r_{3} - r_{1} - r) + λ r_{1}^{2} l n (\frac{r}{r_{1}}) = H_{1}^{2} \\ r_{1} \leq r \leq r_{2} \end{array}

(8)

由于浸润线在渗出点B处与下游坡面相切^[30],即B点应该满足以下2个条件

H_{2} = t a n α \cdot (r_{3} - r_{2})

(9)

J_{B} = - \frac{d H}{d r} |_{r = r_{2}} = s i n α

(10)

式（9）、式（10）中：H₂为出渗点B（r = r₂）处水头数值,单位m；r₃为C点坐标数值,单位m；α为出渗点B处的坡度数值,单位（°）；J_B为出渗点B处水力梯度。

将式（10）及点（r₂, H₂）代入式（8）,并联合式（9）,可得

r_{2} = \frac{1}{2} \{r_{3} + \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot [t a n α - t a n β]}}\}

(11)

H_{2} = \frac{t a n α}{2} \cdot \{r_{3} - \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot [t a n α - t a n β]}}\}

(12)

由于H₁＞H₂＞0,定f₁=tanβ·（2r₃-r₁-r₂）,将点（r₂, H₂）代入式（11）,可得

H_{1} = \frac{1}{2} \{f_{1} + \sqrt[]{f_{1}^{2} + 4 [H_{2}^{2} + 2 λ r_{1}^{2} l n (\frac{r_{2}}{r_{1}}) - f_{1} H_{2}]}\}

(13)

由于H₀＞H₁,定f₂=tanβ·（2r₃-r₁）,将点（r₁, H₁）代入式（6）,可得

H_{0} = \frac{1}{2} [f_{2} + \sqrt[]{f_{2}^{2} + 4 (H_{1}^{2} + \frac{λ r_{1}^{2}}{2} - f_{2} H_{1})}]

(14)

综合式（5）、式（8）—式（14）可得到倾斜底板稳定浸润线方程

\{\begin{array}{l} H^{2} - t a n β \cdot (H - H_{0}) \cdot (2 r_{3} - r) + \frac{λ}{2} r^{2} = H_{0}^{2} 0 \leq r \leq r_{1} \\ H^{2} - t a n β \cdot (H - H_{1}) \cdot (2 r_{3} - r_{1} - r) + λ r_{1}^{2} l n (\frac{r}{r_{1}}) = H_{1}^{2} r_{1} \leq r \leq r_{2} \\ r_{2} = \frac{1}{2} \{r_{3} + \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot [t a n α - t a n β]}}\} \\ H_{2} = \frac{t a n α}{2} \cdot \{r_{3} - \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot [t a n α - t a n β]}}\} \\ H_{1} = \frac{1}{2} \{f_{1} + \sqrt[]{f_{1}^{2} + 4 [H_{2}^{2} + λ r_{1}^{2} l n (\frac{r_{2}}{r_{1}}) - f_{1} H_{2}]}\} \\ H_{0} = \frac{1}{2} [f_{2} + \sqrt[]{f_{2}^{2} + 4 (H_{1}^{2} + \frac{λ r_{1}^{2}}{2} - f_{2} H_{1})}] \end{array}

(15)

式（15）为一般情况下矿山稳定浸润线方程,对于基岩底板水平的情况,令β = 0°,可将式（15）简化为

\{\begin{array}{l} H^{2} + \frac{λ}{2} r^{2} = H_{0}^{2} 0 \leq r \leq r_{1} \\ H^{2} + λ r_{1}^{2} \cdot l n (\frac{r}{r_{1}}) = H_{1}^{2} r_{1} \leq r \leq r_{2} \\ r_{2} = \frac{1}{2} (r_{3} + \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot t a n α}}) \\ H_{2} = \frac{t a n α}{2} \cdot [r_{3} - \sqrt[]{r_{3}^{2} - \frac{2 λ r_{1}^{2}}{s i n α \cdot t a n α}}] \\ H_{1} = \sqrt[]{H_{2}^{2} + λ r_{1}^{2} \cdot l n (\frac{r_{2}}{r_{1}})} \\ H_{0} = \sqrt[]{H_{1}^{2} + \frac{λ r_{1}^{2}}{2}} \end{array}

(16)

根据式（15）,均匀稳定注液入渗（λ＞0）的条件下,注液区的浸润线是椭圆线的上半支,非注液区的浸润线是抛物线与对数曲线组成的复杂形状。令式（15）中的λ = 0、r₁=0（即不注液）,可求得H₀=H₁=H₂=tanβ·r₃,过水断面高度h₀=h₁=h₂=0,与实际情况相符。经验表明,当注液入渗量不足时,基岩面难以形成完整的浸润线。因此,如果得到完整的浸润线,应该满足条件H₀≥tan β·r₃,将该条件代入式（15）,即可求得给定注液范围下的最低注液强度或给定注液强度下的最小注液范围。

2 浸润线计算误差的参数分析

2.1 有限元模型与工况

为了进一步分析浸润线方程式（15）及式（16）的计算误差,根据矿山的地形条件和注液条件,提出4个参数：出渗坡度（α）、基岩坡度（β）、注液范围（r₁²/r₃²）和相对渗透系数（λ）,按图3简化模型建立有限元模型,将有限元计算结果作为对照值,分析上述4个参数对浸润线方程计算误差的影响规律。其中,α可根据山脚集液沟设计和施工情况确定；β应根据矿山工程勘探资料给出的地质剖面图确定；r₁²/r₃²根据矿山注液方案中矿体分布情况确定,同时避开边坡坡度陡峭处；λ根据矿山注液方案和土体渗透系数k_s确定,注液方案给出了矿山注液范围的面积A（单位：m²）和注液总强度Q（单位：m³/d）,k_s通过室内、外土体渗透性实验确定,则相对渗透系数λ=Q/（Ak_s）。

矿山建模高度为30 m,长度r₃= 50 m,计算工况见表1。

表 1 计算工况汇总

Table 1. Summary of calculation conditions

参数	取值										工况数
α /（°）	30.96	34.29	36.87	41.42	45.00	51.34	56.31	63.43^*	71.57	82.41	10
β /（°）	0	2.29	4.57	7.97^*	10.20	12.41	14.57	—	—	—	7
r₁²/r₃²	0.01	0.04	0.09	0.16	0.25^*	0.36	0.49	—	—	—	7
λ	0.04	0.08	0.12	0.16	0.20^*	0.24	0.28	0.32	0.36	—	9
注：“—”现场资料未提供数据；标有“*”的为模型参数的基本值,即：进行某一个参数的敏感性分析时,该参数按表1中数据从小到大取值,另外3个参数则取基本值。

下载: 导出CSV

| 显示表格

2.2 计算误差参数分析

典型工况（各参数均取基本值）下,浸润线对比分析如图4所示。由图4可知,方程计算浸润线基本位于数值计算浸润线之上,但两者非常接近,其计算误差沿流场方向逐渐增大,即注液段误差最小,中间段误差次之,出渗段（出渗点附近）误差最大；但在出渗点处,方程计算浸润线却位于数值计算浸润线之下。这是因为：本文浸润线方程的推导引入了Dupuit假定,该假定在地下分水岭附近及出渗点附近并不满足^[29],分水岭附近,垂向流速较大,铅垂面十分接近流面,不能假定为等水头面,Dupuit假定忽略了垂向流速,因此,公式计算值一般要比实际值偏大；出渗段等水头面往往比较弯曲,水力梯度逐渐变大,以利地下水渗出成为地表水,并产生“水跃”现象,而Dupuit假定不能考虑“水跃”现象,且本文浸润线方程在出渗点处满足浸润线与出渗边坡相切的条件,造成浸润线在该处“弯曲”严重,因此,公式计算值一般要比实际值更小。

图 4 典型工况下浸润线对比

Figure 4. Comparison chart of steady seepage lines under typical working conditions

下载: 全尺寸图片幻灯片

为进一步分析各参数对不同部位浸润线方程计算结果的影响,下面以分水岭（r = 0 m）、中间点（r₁²/r₃² = 0.5）与出渗点（r = r₂）分别分析4个参数对浸润线方程计算误差的影响规律。

浸润线计算误差随出渗坡度的变化曲线如图5所示,由图5可知：浸润线计算值在分水岭及中间点较数值解偏大,且随出渗坡度的增大而小幅增大,误差最大值为11.42%；浸润线计算值在出渗点较数值解偏小,且误差的绝对值随出渗坡度的增大呈现先增大后减小的变化趋势,当出渗坡度α=41.42°时,误差最小值为-13.51%。由于修建集液沟时会挖除坡脚表层黏土,出渗坡度α一般较大,因此,出渗坡度α对浸润线计算误差较小。

图 5 浸润线计算误差随出渗坡度的变化曲线

Figure 5. The changing curve of calculation error with the seepage gradient

下载: 全尺寸图片幻灯片

浸润线计算误差随基岩坡度的变化曲线如图6所示,由图6可知：浸润线计算值在分水岭及中间点较数值解偏大,在出渗点较数值解偏小,且误差的绝对值随基岩坡度的增大近似线性增大,该误差的产生是由于本文浸润线方程中水力梯度的计算忽略了基岩坡度的影响,而采用水平距离近似表示渗流长度,因此基岩坡度越大,误差越大。由于原地浸矿基岩坡度一般较小（β＜15°）,因此,出渗坡度对浸润线计算误差的影响较小。

图 6 浸润线计算误差随基岩坡度的变化曲线

Figure 6. The changing curve of calculation error with the gradient of bed rock

下载: 全尺寸图片幻灯片

浸润线计算误差随注液范围和相对渗透系数的变化曲线分别如图7和图8所示,由图7和图8可知：浸润线计算误差随注液范围和相对渗透系数具有类似的变化规律,即误差的绝对值随着注液范围或相对渗透系数的增大而减小。定义矿山相对注液强度W_r为矿山实际注液流量与矿山总面积下饱和注液流量之比,即W_r= λ·r₁²/r₃²,可知,图7和图8均反映的是浸润线方程计算误差随矿山相对注液强度W_r的变化规律,当相对注液强度W_r很小时,矿山基岩上甚至不能形成完整的浸润线,此时浸润线计算误差较大,这种情况只发生在原地浸矿注液初期；在注液稳定期,矿山相对注液强度W_r较大,矿山基岩上形成了较高的浸润线,浸润线方程计算误差较小。

图 7 浸润线计算误差随注液范围的变化曲线

Figure 7. The changing curve of calculation error with the range of liquid injection

下载: 全尺寸图片幻灯片

图 8 浸润线计算误差随相对渗透系数的变化曲线

Figure 8. The changing curve of calculation error with the relative permeability coefficient

下载: 全尺寸图片幻灯片

3 结论

1）选取浑圆形裸脚式稀土矿山为研究对象,建立原地浸矿“注液-收液”轴对称简化模型,基于地下水动力学和Dupuit假定,推导得到矿山稳定浸润线方程,方程以分段函数表示,其中注液区的浸润线是椭圆线的上半支,非注液区的浸润线是抛物线与对数曲线组成的复杂形状。

2）以有限元计算结果为对照值,分析出渗坡度、基岩坡度、注液范围和相对渗透系数等参数对浸润线方程计算误差的影响,发现方程计算浸润线基本位于数值计算浸润线之上,但两者非常接近,其计算误差沿流场方向逐渐增大,但对于原地浸矿而言,各参数取值对方程计算误差的影响较小。

3）原地浸矿浸润线的高低与形状是矿山“注液-收液”渗流场形成与发展的结果,同时浸润线的高低与形状又跟矿山边坡稳定性、矿体浸泡体积百分比及资源浸取率等密切相关,因此浸润线方程可为原地浸矿“注液-收液”浸渗环节的“事先预测（设计）”提供理论依据。

4）浸润线方程的求解需要确定地形条件（α、β和r₃）和注液条件（r₁和λ）,模型参数比较多,某些参数不易获取,且模型和参数均作了一定程度上的简化,计算结果应充分评估后使用。

图 1 二次铝灰XRD图谱

Fig 1. XRD pattern of the secondary aluminum dross

下载: 全尺寸图片幻灯片

图 2 制备材料过程示意

Fig 2. Schematics of the materials prepared by the secondary aluminium dross

下载: 全尺寸图片幻灯片

图 3 MgAl₂O₄形成机制：Al³⁺和Mg²⁺反向扩散

Fig 3. Spinel formation mechanism through the counter-diffusion of Al³⁺ and Mg²⁺ cation

下载: 全尺寸图片幻灯片

图 4 不同配比镁铝尖晶石材料的XRD图谱

Fig 4. XRD patterns of spinel with different proportions

下载: 全尺寸图片幻灯片

图 5 不同烧结温度镁铝尖晶石材料的XRD图谱

Fig 5. XRD patterns of spinel at different sintering temperatures

下载: 全尺寸图片幻灯片

图 6 不同烧结温度，烧结3 h镁铝尖晶石材料粉体的SEM像

Fig 6. SEM images of spinel powders at different sintering temperatures for 3 h

下载: 全尺寸图片幻灯片

图 7 1 400 ℃烧结3 h试样粉料微区线扫描和面扫描像

Fig 7. Line and mapping scan analysis of MgAl₂O₄ spinel powders at 1 400 ℃ for 3 h

下载: 全尺寸图片幻灯片

图 8 不同烧结温度镁铝尖晶石材料粉体的FTIR和Raman谱

Fig 8. FTIR and Raman images of spinel powders at different sintering temperatures

下载: 全尺寸图片幻灯片

图 9 不同烧结温度材料显气孔率和体积密度

Fig 9. Apparent porosity and density of spinel at different sintering temperatures

下载: 全尺寸图片幻灯片

图 10 不同烧结温度镁铝尖晶石材料线变化率和抗压强度

Fig 10. Linear expansivity and compressive strength of spinel at different sintering temperatures

下载: 全尺寸图片幻灯片

表 1 二次铝灰化学成分

Table 1 Chemical compositions of the secondary aluminum dross

下载: 导出CSV

表 2 不同烧结温度镁铝尖晶石材料粉体的拉曼光谱峰

Table 2 Raman peaks in MgAl₂O₄ spinel at different sintering temperatures

下载: 导出CSV

参考文献(27)

[1]	焦占忠, 张凤炳, 赵刚. 铝灰的资源化利用前景广阔[J]. 资源再生, 2018(10): 34-35. doi: 10.3969/j.issn.1673-7776.2018.10.012
[2]	杨航, 申士富, 刘海营, 等. 二次铝灰工艺矿物学特性研究[J]. 有色金属工程, 2019, 9(10): 117-125. https://www.cnki.com.cn/Article/CJFDTOTAL-YOUS201910017.htm
[3]	杜永立. 中国再生铝产业状况及发展趋势[J]. 有色金属再生与利用, 2004(1): 35-37. https://www.cnki.com.cn/Article/CJFDTOTAL-JSZS200401014.htm
[4]	MANFREDI O, WUTH W, BOHLINGER I. Characterizing the physical and chemical properties of aluminum dross[J]. JOM, 1997, 49(11): 48-51. doi: 10.1007/s11837-997-0012-9
[5]	李玲玲, 宋明, 靳强. 铝灰回收利用的研究进展[J]. 无机盐工业, 2018, 50(8): 6-11. https://www.cnki.com.cn/Article/CJFDTOTAL-WJYG201808002.htm
[6]	TAVANGARIAN F, EMADI R. Synthesis and characterization of pure nanocrystalline magnesium aluminate spinel powder[J]. Journal of Alloys and Compounds, 2010, 489(2): 600-604. doi: 10.1016/j.jallcom.2009.09.120
[7]	BONNEFONT G, FANTOZZI G, TROMBERT S, et al. Fine-grained transparent MgAl₂O₄ spinel obtained by spark plasma sintering of commercially available nanopowders[J]. Ceramics International, 2012, 38(1): 131-140. doi: 10.1016/j.ceramint.2011.06.045
[8]	周玉军, 唐建洪, 唐大才, 等. 镁铝尖晶石质耐火材料的开发与应用[J]. 中国金属通报, 2018(8): 193-194. https://www.cnki.com.cn/Article/CJFDTOTAL-JSTB201808119.htm
[9]	MASCHIO R D, FABBRI B, FIORI C. Industrial applications of refractories containing magnesium aluminate spinel[J]. Industrial Ceramics, 1988, 8(3): 121-126.
[10]	TSAKIRIDIS P E. Aluminium salt slag characterization and utilization--A review[J]. Journal of Hazardous Materials, 2012, 217-218(6): 1-10. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0304389412003317&originContentFamily=serial&_origin=article&_ts=1428724546&md5=a92f4184a35c976c633a5bfb376afa59
[11]	张勇, 郭朝晖, 王硕, 等. 响应曲面法对铝灰中AlN的水解行为[J]. 中国有色金属学报, 2016, 26(4): 919-928. https://www.cnki.com.cn/Article/CJFDTOTAL-ZYXZ201604025.htm
[12]	张勇, 郭朝晖, 王硕, 等. 二次铝灰烧结制备钙铝黄长石/镁铝尖晶石复相材料[J]. 中国有色金属学报, 2018, 28(2): 334-349. https://www.cnki.com.cn/Article/CJFDTOTAL-ZYXZ201802015.htm
[13]	郭海军, 尚宏志, 刘希文, 等. 油墨用氧化铝合成方法[J]. 辽宁化工, 2000, 29(5): 274-275. https://www.cnki.com.cn/Article/CJFDTOTAL-LNHG200005008.htm
[14]	刘晓红, 刘守信, 邹美琪, 等. 从铝灰中回收铝制备超细氧化铝粉体过程研究[J]. 轻金属, 2009(12): 18-20. https://www.cnki.com.cn/Article/CJFDTOTAL-QJSS200912004.htm
[15]	李菲, 郭学益, 田庆华. 二次铝灰制备α-Al₂O₃工艺[J]. 北京科技大学学报, 2012, 34(4): 383-389. https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201204004.htm
[16]	刘大强, 刘桂媛, 何云龙. 铝灰生产棕刚玉的工艺[J]. 哈尔滨理工大学学报, 1996, 1(2): 48-50. https://www.cnki.com.cn/Article/CJFDTOTAL-HLGX199605011.htm
[17]	刘瑞琼, 智利彪, 智国彪. 利用铝灰低温冶炼制备棕刚玉[J]. 耐火材料, 2014, 48(2): 145-146. https://www.cnki.com.cn/Article/CJFDTOTAL-LOCL201402020.htm
[18]	ZHANG Y, GUO Z H, HAN Z Y, et al. Effects of AlN hydrolysis on fractal geometry characteristics of residue from secondary aluminium dross using response surface methodology[J]. Transactions of Nonferrous Metals Society of China, 2018, 28(12): 2574-2581. http://www.sciencedirect.com/science/article/pii/S1003632618649040
[19]	DEAN J A. 兰氏化学手册[M]. 北京: 科学出版社, 2003.
[20]	JIA X L, ZHANG H J, YAN Y J, et al. Effect of the citrate sol-gel synthesis on the formation of MgAl₂O₄ ultrafine powder[J]. Materials Science and Engineering: A, 2004, 379(1/2): 112-118. http://www.sciencedirect.com/science/article/pii/S002554080400025X
[21]	ZHANG Y, GUO Z H, HAN Z Y, et al. Feasibility of aluminum recovery and MgAl₂O₄ spinel synthesis from secondary aluminum dross[J]. International Journal of Minerals, Metallurgy and Materials, 2019, 26(3): 309-318. http://www.cqvip.com/QK/85313X/201903/7001423242.html
[22]	BRAULIO M A L, RIGAUD M, BUHR A, et al. Spinel-containing alumina-based refractory castables[J]. Ceramics International, 2011, 37(6): 1705-1724. http://www.onacademic.com/detail/journal_1000034061655310_adc5.html
[23]	BAFROOEI H B, EBADZADEH T. MgAl₂O₄ nanopowder synthesis by microwave assisted high energy ball-milling[J]. Ceramics International, 2013, 39(8): 8933-8940. http://www.researchgate.net/profile/Hadi_Barzegar-Bafrooei/publication/276945134_MgAl2O4_nanopowder_synthesis_by_microwave_assisted_high_energy_ball-milling/links/5649634808aef646e6d2354e.pdf
[24]	GUO J J, LOU H, ZHAO H, et al. Novel synthesis of high surface area MgAl₂O₄ spinel as catalyst support[J]. Materials Letters, 2004, 58(12/13): 1920-1923. http://www.onacademic.com/detail/journal_1000035416376410_bb3a.html
[25]	ZAWRAH M F, HAMAAD H, MEKY S. Synthesis and characterization of nano MgAl₂O₄ spinel by co-precipitated method[J]. Ceramics International, 2007, 33(6): 969-978. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0272884206000976&originContentFamily=serial&_origin=article&_ts=1473910724&md5=0625707d2dcd746ad207968938a8cf2a
[26]	MINH N V, YANG I S. A Raman study of cation disorder transition temperature of natural MgAl₂O₄ spinel[J]. Vibrational Spectroscopy, 2004, 35(1/2): 93-96. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0924203103002121&originContentFamily=serial&_origin=article&_ts=1493699634&md5=50d8f6056301e3a2f8864cd1e9f3ba2d
[27]	BARPANDA P, BEHERA S K, GUPTA P K, et al. Chemically induced order disorder transition in magnesium aluminium spinel[J]. Journal of the European Ceramic Society, 2006, 26(13): 2603-2609. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0955221905004838&originContentFamily=serial&_origin=article&_ts=1476743954&md5=f7abf44a7d57609237db662490d5736a

施引文献(3)

期刊类型引用(2)

1.	刘德峰，张世佳，张臻悦，郭文达，池汝安. 风化壳淋积型稀土矿浸润线空间分布特征及影响因素敏感性分析. 稀土. 2025(01): 1-13 . 百度学术
2.	王忠锋，冯羽生，黄伟玲. 不同结构组态对导流筒搅拌槽混合效率影响分析. 有色金属科学与工程. 2024(06): 814-821+855 . 本站查看

其他类型引用(1)

资源附件(0)

图(10) / 表(2)

计量

文章访问数: 164
HTML全文浏览量: 73
PDF下载量: 12
被引次数: 3

1 浑圆形裸脚式矿山原地浸矿稳定浸润线理论分析
1.1 矿山“注液-收液”轴对称简化模型
1.2 稳定浸润线方程的推导
2 浸润线计算误差的参数分析
2.1 有限元模型与工况
2.2 计算误差参数分析
3 结论

二次铝灰烧结制备镁铝尖晶石材料

通讯作者: 张勇（1989—），男，博士，讲师，主要从事固体废物资源化利用方面的研究。E-mail：752607795@qq.com

计量

出版历程