A first principle study on the basic properties of inclusions in aluminum alloy
-
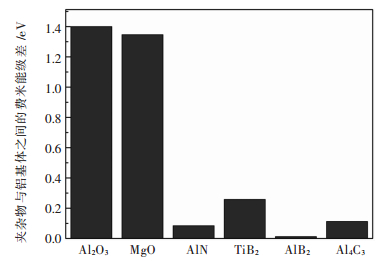
摘要: 采用第一性原理计算的方法研究了铝合金基体及常见夹杂物Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的基本性质.形成热的计算结果表明Al2O3最容易形成，其次是MgO，AlB2相对最难形成；Al2O3、AlN、TiB2结合能的绝对值稍微大于其他物相，且TiB2最稳定，AlB2相对最不稳定；TiB2粒子的切变模量、体模量、杨氏模量和硬度均最高，Al4C3与基体硬度最接近，表明TiB2粒子对铝合金强度、刚度、加工性能的影响最大；AlN粒子的各向异性因子最大，其对铝合金各向异性的影响最大，AlB2次之，Al2O3和TiB2粒子对铝合金各向异性程度影响较小；TiB2对铝合金韧性的影响最大，AlN次之，Al4C3对铝合金韧性的影响最小；Al2O3与铝基体之间的相对费米能级差较大，为1.4 eV，而AlB2粒子最小，各夹杂物对材料腐蚀性能的影响大小顺序为：Al2O3>MgO>TiB2>Al4C3>AlN>AlB2.Abstract: The basic properties of aluminum alloy matrix and common inclusions of Al2O3, MgO, AlN, TiB2, AlB2, Al4C3 in aluminum alloy were studied by means of first principles calculation. The formation heat reveals that Al2O3 is the easiest to form, while MgO and AlB2 are the most difficult to form. The absolute value of binding energy of Al2O3, AlN and TiB2 are slightly larger than others, which suggests that TiB2 is the most stable particle while AlB2 is the most unstable one. TiB2 holds the highest shear modulus, bulk modulus, Young's modulus and hardness. The hardness of Al4C3 is the closest one to aluminum alloy matrix, which indicates that TiB2 has the largest impact on the strength, stiffness and processing performance of aluminum alloy. The anisotropy factor of AlN particles is the largest, and its influence on that of aluminum alloy is also the largest, then followed by AlB2. The influence of Al2O3 and TiB2 particles on the anisotropy of aluminum alloy is small. The impact of TiB2 on the toughness of aluminum alloy is the greatest, followed by AlN, and Al4C3 is the smallest. The relative Fermi difference between Al2O3 and aluminum matrix is the largest, i.e. 1.4eV. AlB2 particle is the smallest. The influence of the studied inclusions on corrosion properties of materials is in the order of Al2O3>MgO>TiB2>Al4C3>AlN>AlB2.
-
Keywords:
- first principles /
- aluminum alloy /
- inclusions /
- basic propertie
-
0 引言
某铜矿采用下向进路尾砂胶结充填法采矿，进路空间位置布置的不同是影响采场稳定性的重要因素[1-2].为给矿山提供不同采矿进路布置方案开采稳定性，采用ANSYS和FLAC3D数值模拟软件进行不同采矿进路布置条件下采场稳定性数值模拟分析，进而指导现场施工[3-5].
1 不同采矿进路布置方案
某铜矿矿体赋存条件复杂，其中下盘围岩中等稳固，上盘围岩为强风化岩组，极不稳固.现场施工工程实践表明，采矿进路与矿岩体空间位置关系可分为3种：
（1）方案1：垂直矿体走向与上、下盘接触；
（2）方案2：沿矿体走向与下盘接触；
（3）方案3：沿矿体走向与上盘接触.
不同采矿进路布置示意图见图 1.
2 数值模拟计算模型
2.1 计算模型
本次数值模拟采用ANSYS三维有限元数值模拟软件建立单元模型，然后导入到FLAC3D有限差分数值模拟软件中进行运算分析[6-9].依据工程概况，模型几何尺寸见表 1，计算模型共划分为101 141个单元，共计18 160个节点，计算模型见图 2，隐藏上盘后模型见图 3，开采进路模型见图 4.
表 1 模型几何尺寸
2.2 地应力场及模型边界条件的确定
将模型顶部边界采用自由边界，模型底部边界采用垂直方向的位移约束.模型的前后、左右采用水平方向的位移约束，模型的原岩应力场由自重应力场作用自动生成.
2.3 矿岩力学参数
经相应折减换算后，模拟矿岩及充填体的物理力学参数见表 2.
表 2 矿岩及充填体物理力学参数
2.4 介质力学模型与破坏准则
本分析将围岩、矿体及充填体均视为各向同性的弹性连续介质.建立模型后，使用Mohr-Coulomb准则作为岩体的破坏准则，Mohr-Coulomb准则的剪切破坏判据如式（1）、式（2）所示：
(1) 其中，
(2) 式（1）、式（2）中：σ1为最大主应力（压应力为负值）；σ3为最小主应力；c为黏结力（或内聚力）；φ为内摩擦角. f为破坏判断系数，当f≥0时，材料处于塑性流动状态；当f≤0时，材料处于弹性变形阶段.
在模拟过程中，模型变形设置为大变形.
3 模拟过程结果分析
按采矿进路与矿岩体空间位置关系的不同分3种方案进行计算，通过数值模拟得到进路回采后矿岩体及充填体的最大与最小主应力结果，将数值计算结果进行比较.具体模拟结果见图 5~图 7.
通过分析方案1、方案2和方案3的最大及最小主应力云图，见图 5~图 7.从图 5可以看出，进路开挖后应力集中区域为顶板和进路端部.其中顶板主要受拉应力控制，其最大拉应力值为0.078~0.389 MPa，该值小于充填体抗拉强度，说明充填体可以维持开挖后进路顶板的稳定性.进路前后两端及两帮受压应力控制，进路端部压应力集中程度较高，端部底角最大压应力大小为2 MPa，两帮压应力大小为0.75 MPa.
从图 6可以看出顶板中间与充填体侧帮顶角之间的区域受拉应力影响，最大拉应力值为0.1~0.15 MPa，而充填体侧帮受压应力影响，最大受压值为1.4~1.5 MPa.以上数值小于充填体自身强度，这表明进路将处于较安全的环境下[10-12].
分析图 7表明进路开挖后应力主要集中在顶板和进路的强风化侧帮顶角和底角处.顶板最大受拉应力值为0.2~0.36 MPa，软岩侧帮底角最大受拉值为0.4~0.56 MPa.充填体及矿岩体抗压不抗拉，易发生破坏.进路两侧帮出现压应力集中尖点，最大受压值可达10~10.6 MPa，超过充填体及强风化岩体的强度值.在此情况下，采场极可能发生严重片帮，进而可能导致顶板垮塌[13-14].
综合模拟过程中的最大与最小主应力分析可得：采矿进路布置沿矿体走向与上盘接触的开采稳定性程度最低，不宜采用[15].
4 小结
（1）对某铜矿不同采矿进路布置开采方案稳定性的数值模拟分析，可得到针对此矿山不同采矿进路布置方案开采稳定性的程度，避开稳定性程度最差的进路布置开采方案；
（2）通过分析可知数值模拟可以作为一种有效的手段确定此矿山不同采矿进路布置方案开采稳定性，进而指导现场施工.
-
![]()
图 1 铝及各夹杂物的晶体模型
Fig 1. Crystal structure of (a) Al, (b) Al2O3, (c) MgO, (d) AlN, (e) TiB2 (f), AlB2 and (g) Al4C3
![]()
图 2 Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的切变模量（G）、体模量（B）、杨氏模量（E）
Fig 2. The shear modulus (G), bulk modulus (B) and Young's modulus (E) of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
![]()
图 3 Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的B/G值、泊松比（v）、各向异性因子（A）
Fig 3. The B/G value, Poisson's ratio(v), the anisotropy index (A) of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
![]()
图 4 Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的维氏硬度
Fig 4. The Vikers Hardness (HV) of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
![]()
图 5 Al2O3、MgO、AlN、TiB2、AlB2、Al4C3与Al之间费米能级差
Fig 5. The D-value of Fermi energy between Al and Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
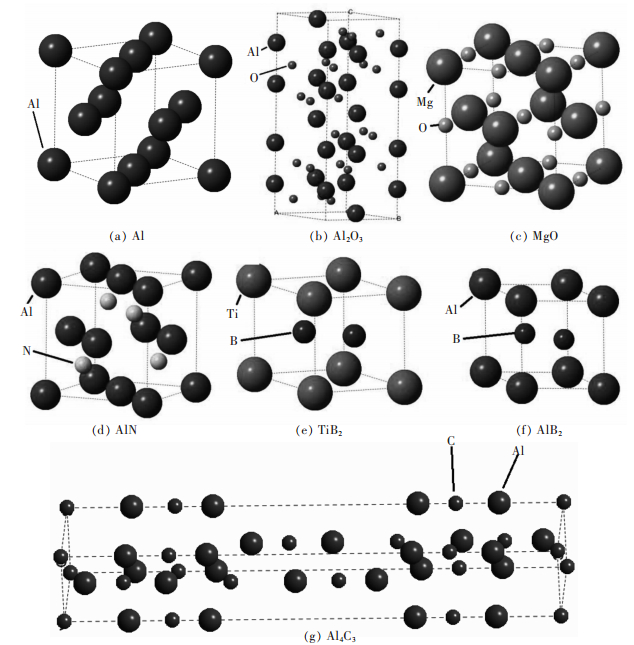
表 1 Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的空间点群、空间点群号、晶系、晶格常数以及原子位置
Table 1 The space group, SG number, crystal system, lattice parameters and atom positions of Al2O3, MgO, AlN, TiB2, AlB2 and Al4C3
下载: 导出CSV
表 2 Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的截断能、K点设置及总能
Table 2 Cut off, K-point settings and total energy of Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
下载: 导出CSV
表 3 几何优化后Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的晶格常数
Table 3 Calculated lattice parameters of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3
下载: 导出CSV
表 7 计算所得及文献报道的Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的弹性常数
Table 7 Calculated elastic constants Cijs(GPa) of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3, along with other theoretical and experimental data
下载: 导出CSV
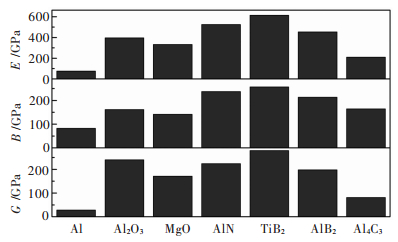
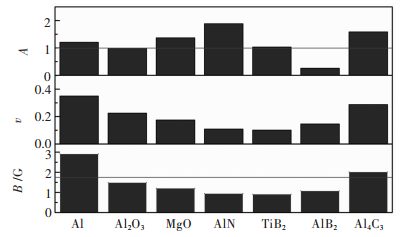
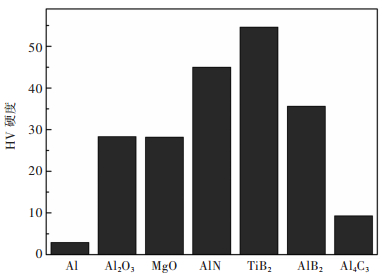
表 8 计算所得及文献报道的Al、Al2O3、MgO、AlN、TiB2、AlB2、Al4C3的剪切模G、体模量B、杨氏模量E、泊松比ν、各向异性因子A以及维氏硬度HV
Table 8 Calculated elastic properties of shear modulus G(GPa), bulk modulus B(GPa), Young's modulus E(GPa), Poisson's ratio(v), the anisotropy index A and Vikers Hardness HV(GPa) of Al, Al2O3, MgO, AlN, TiB2, AlB2, Al4C3, along with other theoretical and experimental data
下载: 导出CSV
-
[1] 刘兵, 彭超群, 王日初, 等.大飞机用铝合金的研究现状及展望[J].中国有色金属学报, 2010, 20(9):1705-1715. http://d.old.wanfangdata.com.cn/Periodical/zgysjsxb201009008 [2] 方华婵, 陈康华, 巢宏, 等. Al-Zn-Mg-Cu系超强铝合金的研究现状与展望[J].粉末冶金材料科学与工程, 2009, 14(6):351-358. doi: 10.3969/j.issn.1673-0224.2009.06.001 [3] 陈亚莉.铝合金在航空领域中的应用[J].有色金属加工, 2003(2):11-14. doi: 10.3969/j.issn.1671-6795.2003.02.003 [4] 赵维.铝合金中夹杂物研究[D].南宁: 广西大学, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1319257 [5] TODA H, KOBAYASHI T, TAKAHASHI A. Mechanical analysis of toughness degradation due to premature fracture of course inclusions in wrought aluminium alloys[J]. Materials Science and Engineering: A, 2000, 280(1):69-75. http://www.sciencedirect.com/science/article/pii/S0921509399006589
[6] 丛红日, 边秀房.铝合金熔体中夹杂物与含氢量的关系[J].特种铸造及有色合金, 2000(3):21-22. doi: 10.3321/j.issn:1001-2249.2000.03.008 [7] 陈发勤.铝合金新型复合熔体精炼剂制备及应用研究[D].南昌: 南昌大学, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1942843 [8] 张淑婷, 王磊, 杨晓华, 等.铝合金熔体净化的研究[J].材料导报, 2009, 23(21):43-45. doi: 10.3321/j.issn:1005-023X.2009.21.010 [9] 石宝东, 潘复生, 陈先华, 等.铝合金熔体净化工艺的研究进展[J].材料导报, 2009, 23(7):45-48. doi: 10.3321/j.issn:1005-023X.2009.07.012 [10] 李杰华, 郝启堂.铝合金熔体净化技术的现状及其发展趋势[J].中国铸造装备与技术, 2005(6):1-4. doi: 10.3969/j.issn.1006-9658.2005.06.001 [11] KONDO S, TATEISHI K, ISHIZAWA N. Structural evolution of corundum at high temperatures[J]. Japanese Journal of Applied Physics, 2008, 47(47):616-619. http://adsabs.harvard.edu/abs/2008jajap..47..616k
[12] CHEN X, KANG J. The structural properties of wurtzite and rocksalt MgxZn1-xO[J]. Semiconductor Science & Technology, 2008, 23(2):025008. http://adsabs.harvard.edu/abs/2008SeScT..23b5008C
[13] JIAO Z Y, MA S H, YANG JF. A comparison of the electronic and optical properties of zinc-blende, rocksalt and wurtzite AlN: A DFT study[J]. Solid State Sciences, 2011, 13(2):331-336. http://www.sciencedirect.com/science/article/pii/S1293255810004693
[14] ANISHCHIK V M, DOROZHKIN N N. Electronic structure of TiB2 and ZrB2[J]. Physica Status Solidi, 1990, 160(160):173-177. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1302.2144
[15] KUMAR G S V, MURTY B S, CHAKRABORTY M. Settling behaviour of TiAl3, TiB2, TiC and AlB2 particles in liquid Al during grain refinement[J]. International Journal of Cast Metals Research, 2010, 23(4):193-204. doi: 10.1179/136404610X12665088537491
[16] GESING T M, JEITSCHKO W. Crystal structure and chemical properties of U2Al3C4 and structure refinement of Al4C3[J]. Cheminform, 1995, 26(26):196-200. doi: 10.1002/chin.199526002/full
[17] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B Condensed Matter, 1999, 59(3):1758-1775. doi: 10.1103/PhysRevB.59.1758
[18] KRESSE G, HAFNER J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements[J]. Journal of Physics: Condensed Matter, 1994, 6(40):8245. doi: 10.1088/0953-8984/6/40/015
[19] ZOPE R R, MISHIN Y. Interatomic potentials for atomistic simulations of the Ti-Al system[J]. Physical Review B, 2003, 68(2):024102. doi: 10.1103/PhysRevB.68.024102
[20] SHEIN I R, IVANOVSKⅡ A L. Elastic properties of mono-and polycrystalline hexagonal AlB2-like diborides of s, p and d metals from first-principles calculations[J]. Journal of Physics Condensed Matter, 2008, 20(41):8106-8110. doi: 10.1088-0953-8984-20-41-415218/
[21] PENG F, FU H Z, CHENG X L. First-principles calculations of thermodynamic properties of TiB2 at high pressure[J]. Physica B Physics of Condensed Matter, 2007, 400(1):83-87. http://www.sciencedirect.com/science/article/pii/S092145260700470X
[22] SUZUKI M, UENOYAMA T, YANASE A. First-principles calculations of effective-mass parameters of AlN and GaN[J]. Physical Review B Condensed Matter, 1995, 52(11):8132. doi: 10.1103/PhysRevB.52.8132
[23] MORIWAKE H. First-principles calculation of formation energy of neutral point defects in perovskite-type BaTiO3[J]. International Journal of Quantum Chemistry, 2004, 99(5):824-827. doi: 10.1002/(ISSN)1097-461X
[24] FU C L, WANG X, YE Y Y, et al. Phase stability, bonding mechanism, and elastic constants of Mo5Si3 by first-principles calculation[J]. Intermetallics, 1999, 7(2):179-184. doi: 10.1016/S0966-9795(98)00018-1
[25] TANAKA I, OBA F, TATSUMI K, et al. Theoretical formation energy of oxygen-vacancies in oxides[J]. Materials Transactions, 2002, 43(7):1426-1429. doi: 10.2320/matertrans.43.1426
[26] ZhANG H L, HAN Y F, WANG J, et al. An ab initio molecular dynamics study on the structural and electronic properties of AlB2, TiB2 and (Alx, Ti(1-x))B2 in Al-Ti-B master alloys[J]. Journal of Alloys & Compounds, 2014, 585(3):529-534. http://www.sciencedirect.com/science/article/pii/S0925838813023530
[27] JACOBA M H G, SCHMID F R. Thermodynamic properties and equation of state of fcc aluminum and bcc iron, derived from a lattice vibrational method[J]. Physics & Chemistry of Minerals, 2010, 37(10):721-739. doi: 10.1007/s00269-010-0371-6
[28] YAO H, OUYANG L, CHING W Y. Ab Initio calculation of elastic constants of ceramic crystals[J]. Journal of the American Ceramic Society, 2010, 90(10):3194-3204. doi: 10.1111/j.1551-2916.2007.01931.x/full
[29] KULAKOV G I. Simultaneous measurement of the component of the stress and strain tensors and determination of the elastic constants for a rock[J]. Soviet Mining, 1974, 10(6):659-663. doi: 10.1007/BF02501031
[30] 陈丽. FCC晶体弹性常数的分子动力学模拟及其适用性[J].机械工程学报, 2005, 41(9):46-50. doi: 10.3321/j.issn:0577-6686.2005.09.010 [31] 张彩丽.合金元素对Mg-Li-X强/韧化作用机制的第一性原理研究[D].太原: 太原理工大学, 2011. http://cdmd.cnki.com.cn/article/cdmd-10112-1011082077.htm [32] DONG N, QIAO Y, ZHANG C, et al. Combined experiment and first-principles study of the formation of the Al2O3 layer in alumina-forming austenitic stainless steel[J]. Rsc Advances, 2017, 7(26):15727-15734. doi: 10.1039/C7RA00860K
[33] GHEBOULI B, GHEBOULI M A, FATMI M, et al. First-principles calculations of structural, electronic, elastic and thermal properties of phase M2SiC (M=Ti, V, Cr, Zr, Nb, Mo, Hf, Ta and W)[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(3):915-925. doi: 10.1016/S1003-6326(15)63680-9
[34] YAO H, OUYANG L, CHING W Y. Ab initio calculation of elastic constants of ceramic crystals[J]. Journal of the American Ceramic Society, 2007, 90(10):3194-3204. doi: 10.1111/jace.2007.90.issue-10
[35] SHANG S, WANG Y, LIU Z K. First-principles elastic constants of α-and θ-Al2O3[J]. Applied Physics Letters, 2007, 90(10): 101909-101903. doi: 10.1063/1.2711762
[36] GLADDEN J R, SO J H, MAYNARD J D, et al. Reconciliation of ab initio theory and experimental elastic properties of Al2O3[J]. Applied Physics Letters, 2004, 85(3):392-394. doi: 10.1063/1.1773924
[37] KISI E H, HOWARD C J, ZHANG J. Verification of the elastic constants for-Al2O 3 using high-resolution neutron diffraction[J]. J. Appl. Cryst., 2011, 44(1):216-218. doi: 10.1107/S0021889810049046
[38] BALTACHE H, KHENATA R, SAHNOUN M, et al. Full potential calculation of structural, electronic and elastic properties of alkaline earth oxides MgO, CaO and SrO[J]. Physica B: Condensed Matter, 2004, 344(1/2/3/4):334-342. http://www.sciencedirect.com/science/article/pii/S092145260300961X
[39] MARINELLI F, LICHANOT A. Elastic constants and electronic structure of alkaline-earth chalcogenides. performances of various hamiltonians[J]. Chemical Physics Letters, 2003, 367(3):430-438. http://www.sciencedirect.com/science/article/pii/S0009261402016986
[40] ZHANG H, BUKOWINSKI M S. Modified potential-induced-breathing model of potentials between close-shell ions[J]. Phys. Rev. B, 1991, 44(6):2495-2503. doi: 10.1103/PhysRevB.44.2495
[41] PENG F, CHEN D, FU H, et al. The phase transition and the elastic and thermodynamic properties of AlN: First principles[J]. Physica B: Condensed Matter, 2008, 403(23/24):4259-4263. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1211.0375
[42] HAMA R K. First-principles calculation of the elastic stiffness tensor of aluminium nitride under high pressure[J]. Journal of Physics: Condensed Matter, 1994, 6(38):7617-7632. doi: 10.1088/0953-8984/6/38/004
[43] VERMA U P, BISHT P S. Ab-initio study of AlN in zinc-blende and rock-salt phases[J]. Solid State Sciences, 2010, 12(5):665-669. doi: 10.1016/j.solidstatesciences.2008.12.002
[44] PANDA K B, CHANDRAN K S R. Determination of elastic constants of titanium diboride (TiB) from first principles using FLAPW implementation of the density functional theory[J]. Computational Materials Science, 2006, 35(2):134-150. http://www.sciencedirect.com/science/article/pii/S0927025605001060
[45] SPOOR P S, MAYNARD J D, PAN M J, et al. Elastic constants and crystal anisotropy of titanium diboride[J]. Applied Physics Letters, 1997, 70(15):1959-1961. doi: 10.1063/1.118791
[46] DUAN Y H, SUN Y, GUO Z Z, et al. Elastic constants of AlB2-type compounds from first-principles calculations[J]. Computational Materials Science, 2012, 51(1):112-116. http://www.sciencedirect.com/science/article/pii/S0927025611003946
[47] 王海蕾.Mg-Al合金熔体碳质孕育晶核/基体间界面性质的第一性原理研究[D].广州: 华南理工大学, 2014. http://cdmd.cnki.com.cn/article/cdmd-10561-1014064377.htm [48] GILMAN J J, ROBERTS B W. Elastic constants of TiC and TiB2[J]. Journal of Applied Physics, 1961, 32(7):1405-1405. doi: 10.1063-1.1736249/
[49] MOTT P H, DORGAN J R, ROLAN C M. The bulk modulus and poisson's ratio of "incompressible" materials[J]. Journal of Sound & Vibration, 2008, 312(4/5):572-575 doi: 10.1016/j.jsv.2008.01.026
[50] HENANN D L, ANANND L. Fracture of metallic glasses at notches: effects of notch-root radius and the ratio of the elastic shear modulus to the bulk modulus on toughness[J]. Acta Materialia, 2009, 57(20):6057-6074. doi: 10.1016/j.actamat.2009.08.031
[51] DAALDEROP G H, KELLY P J, SCHUURMANS M F. First-principles calculation of the magnetocrystalline anisotropy energy of iron, cobalt, and nickel[J]. Physical Review B Condensed Matter, 1990, 41(17):11919. doi: 10.1103/PhysRevB.41.11919
[52] KLUGE M D, RAY J R, RAHMAN A. Molecular dynamic calculation of elastic constants of silicon[J]. Journal of Chemical Physics, 1986, 85(7):4028-4031. doi: 10.1063/1.450871
[53] LOUAIL L, MAOUCHE D, ROUMILI A, et al. Calculation of elastic constants of 4d transition metals[J]. Materials Letters, 2004, 58(24):2975-2978. doi: 10.1016/j.matlet.2004.04.033
[54] WU Y, HU W, HAN S. First-principles calculation of the elastic constants, the electronic density of states and the ductility mechanism of the intermetallic compounds: YAg, YCu and YRh[J]. Physica B Physics of Condensed Matter, 2008, 403(19):3792-3797. http://www.sciencedirect.com/science/article/pii/S0921452608003104
[55] SINKO G V, SMIRNOV N A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure[J]. Journal of Physics: Condensed Matter, 2002, 14(29):6989-7005. doi: 10.1088/0953-8984/14/29/301
[56] 李昱材, 张国英, 魏丹, 等.金属电极电位与费米能级的对应关系[J].沈阳师范大学学报(自然科学版), 2007, 25(1):25-28. doi: 10.3969/j.issn.1673-5862.2007.01.007 [57] 黄元春, 肖政兵, 张欢欢, 等.平衡相对Al-7.8Zn-1.6Mg-1.8Cu-0.12Zr铝合金性能影响:第一性原理研究[J].航空材料学报, 2014, 34(3):28-34. http://d.old.wanfangdata.com.cn/Periodical/hkclxb201403005 [58] 杨少华, 刘增威, 林明. 7075铝合金在不同pH值NaCl溶液中的腐蚀行为[J].有色金属科学与工程, 2017, 8(4):7-11. http://ysjskx.paperopen.com/oa/DArticle.aspx?type=view&id=201704002 [59] 罗垂意, 李之锋, 彭弯弯.锂离子电池正极材料LixNi0.5Mn0.5O2电子结构的第一性原理研究[J].有色金属科学与工程, 2016, 7(4):45-49. http://ysjskx.paperopen.com/oa/DArticle.aspx?type=view&id=20160408
计量
- 文章访问数: 101
- HTML全文浏览量: 8
- PDF下载量: 12
