Numerical Analysis of Dynamic Damage and Energy Dissipation Characteristics of Concrete under Confining Pressure
-
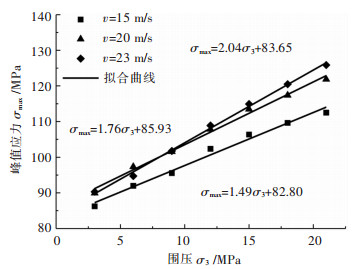
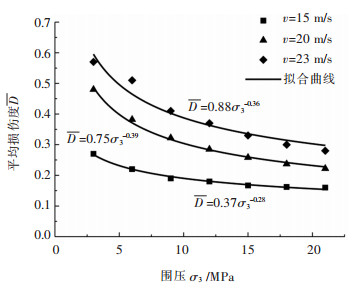
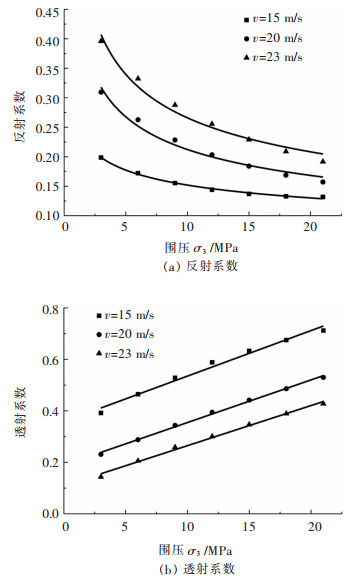
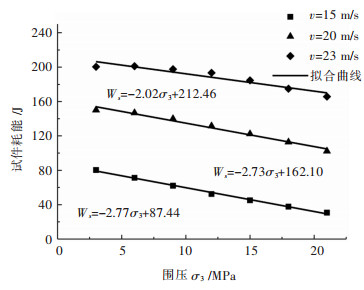
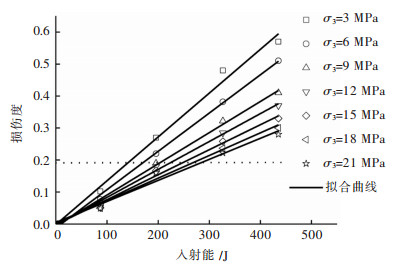
摘要: 为了研究围压对混凝土材料冲击破坏过程中损伤演化和能量耗散的影响，基于ANSYS/LS-DYNA有限元软件，模拟了不同冲击速度和围压级别下的混凝土SHPB实验. 结果表明：在不同的冲击速度下，峰值应力均随着围压的提高线性增大，最大可以达到混凝土静态抗压强度的3~4倍. 围压条件下混凝土的破坏形式为压剪破坏，试件的平均损伤度随围压的增大而非线性降低，相较于冲击速度，围压对损伤度的影响更弱. 随着围压的提高，混凝土对应力波的透射能力增强，反射波的能量非线性降低，而透射能随着围压的增大近似线性增加，混凝土的耗能随着围压的增大而近似线性降低；在不同的入射能下，反射系数、透射系数和试件耗能的变化趋势是一致的. 围压一定时，混凝土的损伤程度随入射能的增加线性增长；入射能一定时，试件损伤度随围压的增加而降低，变化幅度也降低.Abstract: In order to study the effect of confining pressure on damage evolution and energy dissipation of the failure process of concrete under impact, the SHPB experiments of concrete under different impact velocities and different level of confining pressures were simulated based on ANSYS/LS-DYNA finite element software. The results show that the peak stress increases linearly with the increase of confining pressure at different impact velocities, which can reach 3~4 times of the static compressive strength of concrete. Under the condition of confining pressure, the failure mode of concrete is compression-shear failure, and the average damage degree of the specimen decreases nonlinearly with the increase of confining pressure. Compared with the impact velocity, the influence of confining pressure on the damage degree is weaker. With the increase of confining pressure, the transmission capacity of the concrete is enhanced, and the reflected energy decreases nonlinearly, while the transmitted energy increases linearly. The energy dissipation of the concrete decreases linearly with the increasing of the confining pressure. On the other hand, the change trend of the reflection coefficients, transmission coefficients and the energy consumption of the specimen are consistent under different incident energy. When the incident energy is constant, damage degree of specimen decreases with the increasing of confining pressure, meanwhile, the variation range decreases as well.
-
Keywords:
- concrete /
- SHPB with confinement /
- damage /
- peak stress /
- energy dissipation
-
0 引言
我国拥有极其丰富的铝矿资源，铝合金型材已被各领域广泛应用.铝合金型材生产过程中最主导技术以及关键的核心环节是挤压成型[1]，型材质量的好坏决定于模具设计结构与挤压工艺参数，如何选择好的挤压工艺参数和延长挤压模具的寿命已成为各行业亟待解决的问题.型材挤压工艺参数设计是挤压设计中最为关键的要领之一，它主要包括挤压比、挤压速度、挤压温度等要素.挤压工艺参数设计合理与否直接关系到后续型材产品的表面质量以及挤压力大小，以往在对挤压工艺参数的选择上往往是通过反复试用以及经验获得，本文主要是通过对型材挤压过程进行仿真模拟，在试模挤压前利用仿真模拟技术对挤压加工进行模拟，通过改变挤压工艺参数的数值，计算获得实验现场无法获得的型材物理性能.
针对挤压过程的仿真模拟国内外做过类似的研究[2-5]，本次研究就是以某6063空心铝型材挤压加工为研究为对象，以Altair Hyperxtrude软件为仿真模拟载体，基于Taguchi分析方法，获得挤压该型材时的最佳工艺参数配比，为企业生产提供参考，从而提高生产效率.
1 实验研究方法
1.1 Altair Hyperxtrude挤压仿真模拟软件的简介
铝型材挤压成型在铝型材加工领域是一个高压高温以及复杂的非线性、大变形的热-力耦合的塑性成型加工过程，Altair Hyperxtrude是目前全球唯一专业的铝型材挤压仿真模拟软件，同时可以对模具结构进行优化的软件，可以进行正向挤压和反向挤压分析，求解类型有瞬态和稳态2种，hyerxtrude采用了ALE算法，ALE算法是以非线性的纳维叶-斯托克斯方程作为控制方程，有连续性、动量守恒和能量守恒3个基本方程控制[6-9].
连续性方程：
$$ \frac{{\partial \rho }}{{\partial t}} + {c_i}\frac{{\partial \rho }}{{\partial {x_i}}} + \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} = 0 $$ (1) 动量守恒方程：
$$ \rho \left( {\frac{{\partial {v_i}}}{{\partial t}} + {c_i}\frac{{\partial {v_i}}}{{\partial {x_i}}}} \right) = \frac{{\partial {\tau _{ji}}}}{{\partial {x_i}}} + {p_i} $$ (2) 能量守恒方程：
$$ \rho \left( {\frac{{\partial E}}{{\partial t}} + {c_i}\frac{{\partial E}}{{\partial {x_i}}}} \right) = \frac{{\partial {T_{ji}}{v_j}}}{{\partial {x_i}}} + {p_j}{v_j} + \frac{{\partial \left( {{K_{ij}}, {T_j}} \right)}}{{\partial {x_i}}} + {K_0} $$ (3) 式（1）~式（3）中：v为材料的位移；ρ为材料密度；τ为柯西应力；T为热力学温度；E为内能；Kij为热传导系数；K0为单位体积的热源；t为时间；pi为作用于物体上单位质量的体力；ci为物质点相对于网格点的运动速度，即为对流速度.
1.2 Taguchi试验研究方法简介
Taguchi试验设计主要的理论基础是概率论和数理统计，通过Taguchi设计理念可以减少试验次数，通过试验方案对比寻找最佳的工艺参数配比，从而降低成本、提高实际生产效率并获得表面质量和性能最佳的型材产品.Taguchi方法[10-12]利用正交表来选择试验条件和安排试验方案，它的最大优点就是利用最少的试验次数获得最佳的工艺参数，该设计方法是一种简单有效的方法，凭借其设计优点被广泛应用于工程、化工、加工等领域.如图 1所示描述了Taguchi试验设计的一般流程.
信噪比（S/N ratio）作为衡量质量特性的重要依据，用于系统和产品开发.本次研究采用信噪比（S/N ratio）来衡量5个挤压工艺参数对型材截面速度均方差、挤压力的影响规律以及对产品品质特性的影响规律，研究采用静态特性中的望小特性（smaller the better）.为了更好地研究采用望小特性（smaller the better），对于望小质量特性服从Y~N（μ，σ2）分布，可将信噪比定义为S/N用η表示，即η=μ2/σ2，用信噪比来衡量产品特性的稳定性.为了使η更加接近于正态分布，使效应趋于线性可加性，将η值变成分贝（dB）值，即
$$ {\eta _{\rm{s}}} = 10{\rm{lg}}\eta $$ 望小特性希望Y越小越好，即可以认为μ2、σ2越小越好，所以可以将η的值变为
$$ \eta = \frac{1}{{{\mu ^2} + {\sigma ^2}}} $$ 即：$ S/N = {\eta _{\rm{s}}} = 10{\rm{lg}}\eta = 10{\rm{lg}}\left( {\frac{1}{{{\mu ^2} + {\sigma ^2}}}} \right) = {\rm{-}}10{\rm{lg}}\left( {{\mu ^2} + {\sigma ^2}} \right) $
另一种表述方式为：
$$ S/N = \eta = {\rm{ - }}10\lg \left( {\frac{{\rm{1}}}{N}\sum\limits_{i = {\rm{1}}}^N {X_{\rm{i}}^2} } \right) $$ (4) 式（4）中，Xi：表示第i次试验的试验值；i：表示试验的序号；N表示试验总次数.
2 挤压模型
本研究的对象是山东某厂生产的型号为Y8255铝合金型材，该型材截面较复杂，每处壁厚分布不均匀.由于型材截面复杂的分布，相应建立了挤压模具三维图，上模外径为510 mm，厚度为130 mm如图 2，在上模上设有分流孔、分流桥、模芯等，下模如图 3，设有模孔焊合深度为17 mm.
将建立好的上模和下模进行组装，首先将组装好的三维模型图导入Hyperxtrude进行数值模拟，图 4为数值模拟分析模型，然后进行前处理，包括几何处理、网格划分等，在对网格划分时应注意以下3点：①型材最薄截面处至少划分6层单元网格；②对工作带区域划分时，沿挤压正方向至少划分9层单元网格；③自由面和工作带上以三菱柱单元网格形式划分，网格划分的顺序按工作带-焊合室-坯料，其他部分网格以离工作带越远网格单元尺寸越大的规则划分.
3 Altair Hyperxtrude挤压模拟结果分析
上述为初始方案（棒料直径210 mm，棒料、模具、料筒预热温度分布为480 ℃、480 ℃、450 ℃，挤压速度为2 mm/s）挤压仿真结果，图 5~图 8分别示出了挤压型材各部分的流速以及流经各处的速度.理论上[13-15]，坯料在工作带上的流速越均匀挤压制品端面越平齐，从而型材质量更好，从图 5可以看到在平模部分明显快于分流部分，并在壁厚小的地方流速更快，这是因为在平模处孔大供料快，而在分流部分相对供料较慢，由图 6可以明显反映供料速度，图 7是坯料通过分流孔的速度，也就是分流孔的供料速度，从图 7中可以看出在坯料流经各分流孔时的相对速度，通过合理对比，在分流孔分配上起到主导作用，在流速快的地方可以适当减少分流孔面积；其中图 8反映的是坯料流经工作带时的流速，可以看出在平模处的流速要稍高于分流部分的速度.
4 Taguchi试验方法分析
利用Hyperxtrude挤压专用模拟软件分别对试验直交表中32组不同的挤压工艺条件下的挤压过程进行仿真模拟，利用公式：$ VRD = \frac{{\sum\limits_{i = 1}^{\rm{n}} {\frac{{\left| {{v_i}{\rm{-}}\overline v } \right|}}{{\overline v }}} }}{n} $，（vi为型材截面上节点i处材料的流动速度；v所有考察节点的平均速度；n为考察节点的总数）.求出每组中挤压型材截面的速度相对均差VRD，为了获得更接近实际型材截面的VRD，所选取型材截面的所有节点的流出速度.
通过模拟out文件获得挤压力大小，同时利用式（4）计算出VRD、挤压力的信噪比，计算结果如表 1.
表 1 因素水平表Table 1. Factors and levels of experiments挤压工艺参数 水平1 水平2 水平3 水平4 棒料直径A/mm 200 205 210 215 挤压速度B/mm.s-1 1.4 2.0 2.6 3.2 棒料预热温度C/℃ 460 470 480 490 模具预热温度D/℃） 450 460 470 480 料筒预热温度E/℃ 430 440 450 460 试验序号 VRD值 VRD的信噪比 挤压力/t 挤压力的信噪比 1 0.026 5 31.535 1 003.2 -60.028 2 0.020 7 33.681 1 057.0 -60.481 3 0.019 0 34.425 1 055.8 -60.471 4 0.020 9 33.597 1 039.0 -60.332 5 0.020 4 33.807 1 016.5 -60.142 6 0.017 3 35.239 1 113.4 -60.933 7 0.013 8 37.202 1 067.4 -60.567 8 0.013 5 37.393 1 097.5 -60.808 9 0.026 1 31.667 1 018.3 -60.158 10 0.029 9 30.487 1 160.0 -61.289 11 0.018 3 34.751 1 166.5 -61.338 12 0.018 4 34.704 1 232.3 -61.814 13 0.021 9 33.191 1 082.0 -60.685 14 0.020 6 33.723 1 215.2 -61.693 15 0.021 4 33.392 1 237.3 -61.850 16 0.013 6 37.329 1 294.1 -62.239 17 0.025 6 31.835 880.56 -58.895 18 0.020 4 33.807 1 016.3 -60.140 19 0.018 9 34.471 1 094.8 -60.787 20 0.024 9 32.076 1 149.8 -61.212 21 0.024 5 32.217 914.4 -59.223 22 0.016 3 35.756 1 043.2 -60.367 23 0.014 6 36.713 1 137.2 -61.117 24 0.013 9 37.140 1 179.7 -61.435 25 0.024 1 32.360 1 022.3 -60.192 26 0.020 3 33.850 1 086.7 -60.722 27 0.032 1 29.870 1 228.3 -61.786 28 0.026 3 31.601 1 204.3 -61.615 29 0.018 9 34.471 1 060.5 -60.510 30 0.020 7 33.681 1 169.0 -61.356 31 0.024 2 32.324 1 267.8 -62.061 32 0.015 8 36.027 1 300.1 -62.280 通过模拟每组工艺参数条件下的挤压过程，计算获得挤压型材截面速度均方差VRD和挤压力的信噪比，为了准确分析各工艺参数对型材的影响，利用直观分析原理算出不同水平条件下各组工艺参数的信噪比的平均值具体见表 2、表 3.
表 2 不同水平下VRD的平均信噪比Table 2. Average signal-to-noise-ratios of VRD under different levels水平 VRD的平均信噪比 A B C D E 1 33.178 32.635 32.620 34.043 33.713 2 35.683 33.778 34.074 33.192 34.938 3 32.411 34.144 35.007 34.358 33.427 4 34.267 34.983 33.840 33.948 33.463 表 3 不同水平下挤压力的平均信噪比Table 3. Average signal-to-noise-ratios of extrusion force under different levels水平 挤压力的平均信噪比 A B C D E 1 -60.293 -59.979 -61.206 -60.983 -61.063 2 -60.574 -60.873 -61.007 -60.916 -60.957 3 -61.114 -61.247 -60.788 -60.863 -60.835 4 -61.584 -61.467 -60.566 -60.804 -60.711 将表 2、表 3不同水平因素的VRD和挤压力信噪比采用直线图的形式表示出来，结果如图 9、图 10，从图 9、图 10中可以看出不同挤压工艺参数对型材截面速度和挤压力有不同的影响规律，根据经验及理论知识可知：型材流经模具出口处的速度越均匀则型材表面质量越好、型材表面缺陷越少；挤压型材所需挤压力越小，挤压所需能耗越小，挤压过程中模具磨损量也越小.因此本研究目标是减小VRD和降低挤压力，故采用信噪比中的望小特性来评价指标的优劣.原理为：信噪比越大，目标变化越小，结果越好.
![]()
图 10 不同挤压工艺参数对挤压力的影响Figure 10. Effects of different extrusion process parameters on extrusion force5 结论
以Hyperxtrude软件为模拟载体，基于Taguchi试验分析方法对模拟结果进行计算分析，并由直线趋势图以及望小特性信噪比原理得出以下结论：
1）对于型材截面流动均匀程度指标参数，最佳的挤压工艺参数组合为A2B4C3D3E2，即挤压棒料外径为205 mm、挤压垫速度3.2 mm/s、棒料预先加热温度为480 ℃、挤压模具预先加热温度为470 ℃、挤压筒预先加热温度为440 ℃.
2）对于挤压力指标参数，最佳工艺参数组合为A1B1C4D4E4，即棒料外径为200 mm、挤压垫速度为1.4 mm/s、棒料预先加热温度为490 ℃，挤压模具预先加热温度为480 ℃、挤压筒预先加热温度为460 ℃.
3）在实际生产厂家推荐以及经验制定的挤压参数范围内，改变挤压工艺参数对型材截面速度和挤压力有很大影响，其中改变棒料直径、挤压速度和棒料预热温度对其影响最大，可以通过改变其参数来控制型材质量.
6 结论验证
以图 2、图 3模具构造原理加工出实际挤压模具，以上述获得的最佳方案A2B4C3D3E2（型材在模具出口处的流速越均匀型材发生扭拧、翘曲等缺陷就越小）设置挤压工艺参数，首先通过Hyperxtrude进行仿真模拟，获得型材理论形变.然后以上述参数进行实际挤压设计，由华南某厂协助完成试模，选择的挤压设备为1 800 t卧式挤压机如图 11，通过试模获得实际型材制品如图 12.通过对型材制品与有限元模拟结果进行分析，可以得出两者变形趋势较一致，最终获得的型材表面光滑平整，没有出现因过烧而引起的表面斑点；纵向也较平直，没有出现因流速不均匀而引起的弯曲、扭拧、翘曲等宏观缺陷.
-
![]()
图 3 入射杆、透射杆上应力波形（σ3=9 MPa）
Fig 3. The stress waveform of incident bar and transmitted bar (σ3=9 MPa)
![]()
图 4 不同工况下峰值应力的变化
Fig 4. The changes of peak stress under different confining pressures and impact velocities
![]()
图 5 不同冲击速度下试件的损伤云图（σ3=9 MPa）
Fig 5. The damage fringe of specimens under different impact velocities and 9 MPa confining pressure
![]()
图 6 试件平均损伤度与围压的关系
Fig 6. The relation between the average degree of damage and confining pressure
![]()
图 8 不同工况下试件耗能规律
Fig 8. The energy dissipation of concrete species under various confinements and impact velocities
![]()
图 9 不同围压下试件损伤度与入射能的关系
Fig 9. The relation between average degree of specimen and incident energy
表 1 混凝土H-J-C模型参数
Table 1 The parameters of H-J-C model
ρ/(kg·m-3) G/GPa A B C N Sfmax D1 D2 Pc/MPa 2440 14.86 0.79 1.60 0.007 0.61 7.0 0.04 1.0 11.4 μc Pl/MPa μl T/MPa K1/GPa K2/GPa K3/GPa fc/MPa εfmin 0.001 800 0.10 3.63 85 -171 208 34.2 0.01 
下载: 导出CSV
-
[1] 李青松, 徐进, 熊益博, 等.混凝土强度与变形特性的围压效应试验研究[J].建筑结构, 2011, 41(05): 85-88. http://www.cnki.com.cn/Article/CJFDTOTAL-JCJG201105021.htm [2] 陈宗平, 陈宇良, 徐金俊, 等.多轴受力状态下再生混凝土的破坏准则及应力-应变本构关系研究[J].土木工程学报, 2015, 48(12): 23-33. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201512006.htm [3] 张亚栋, 邹宾, 田杨, 等.冻融循环对混凝土静动力特性的影响[J].解放军理工大学学报(自然科学版), 2017, 18(01): 1-8 http://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201701001.htm [4] 梁书锋, 刘殿书, 李洪超, 等.高温后混凝土动态力学性能时间效应试验[J].辽宁工程技术大学学报(自然科学版), 2016, 35(04): 392-397 http://www.cnki.com.cn/Article/CJFDTOTAL-FXKY201604011.htm [5] 韩李斌, 杨黎明.泡沫混凝土动态力学性能及破坏形式[J].宁波大学学报(理工版), 2017, 30(01): 68-72 http://www.cnki.com.cn/Article/CJFDTOTAL-NBDZ201701013.htm [6] 朱靖塞, 许金余, 白二雷, 等.复合纳米材料对混凝土动态力学性能的影响[J].复合材料学报, 2016, (03): 597-605 http://www.cnki.com.cn/Article/CJFDTOTAL-FUHE201603020.htm [7] 薛志刚, 胡时胜.水泥砂浆在围压下的动态力学性能[J].工程力学, 2008, 25(12): 184-188+201. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ200806013.htm [8] 张磊, 何翔, 王晓峰, 等.混凝土恒定围压下冲击加载实验装置研制[J].振动与冲击, 2015, 34(22): 24-27. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201522005.htm [9] 彭刚, 王乾峰, 梁春华.有压孔隙水环境中的混凝土动态抗压性能研究[J].土木工程学报, 2015, 48(01): 11-18 http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201501003.htm [10] 杜修力, 金浏.细观分析方法在混凝土物理/力学性质研究方面的应用[J].水利学报, 2016, 47(03): 355-371 http://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201603013.htm [11] 金浏, 杜修力.基于细观单元等效化方法的混凝土动态破坏行为分析[J].工程力学, 2015, 32(04): 33-40 http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201504006.htm [12] 雷光宇, 韩霁昌, 党发宁, 等.预静载对细观混凝土动态力学特性的数值试验研究[J].水利与建筑工程学报, 2016, 14(03): 55-58 doi: 10.3969/j.issn.1672-1144.2016.03.010 [13] 别雪梦, 李召, 管文强, 等.快速加载下钢管混凝土柱动力性能数值模拟[J].混凝土, 2016, (08): 27-31+35 doi: 10.3969/j.issn.1002-3550.2016.08.007 [14] 惠兴田, 王群.邵寨煤矿立井井壁支护方法的研究[J].煤炭技术, 2017, 36(01): 22-23 http://www.cnki.com.cn/Article/CJFDTOTAL-MTJS201701009.htm [15] 胡昌明, 韩林海.圆形钢管混凝土叠合构件抗冲击性能试验研究[J].土木工程学报, 2016, 49(10): 11-17 http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201610005.htm [16] 李祥龙, 刘殿书, 冯明德, 等.钢质套筒被动围压下混凝土材料的冲击动态力学性能[J].爆炸与冲击, 2009, 29(05): 463-467. doi: 10.3321/j.issn:1001-1455.2009.05.003 [17] ZHANG H, Li F, GAO Y W. Study on the Dynamic Performance of Asphalt Concrete under Passive Confined Pressure [J]. Applied Mechanics and Materials, 2012, 2031(226). https://www.scientific.net/AMM.226-228.1755
[18] 吴赛, 赵均海, 李楠, 等.被动围压下混凝土的动态力学性能研究[J].应用力学学报, 2015, 32(06): 992-998+1103. http://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201506017.htm [19] 周子龙, 李夕兵, 赵国彦, 等.岩石类SHPB实验理想加载波形的三维数值分析[J].矿冶工程, 2005, 25(03): 18—20. doi: 10.3969/j.issn.0253-6099.2005.03.006 [20] 李夕兵, 古德生, 赖海辉.冲击载荷下岩石动态应力-应变全图测试中的合理加载波形[J].爆炸与冲击, 1993, 13(02): 125—130. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ199302004.htm [21] 吕太洪, 陈小伟, 陈刚.基于混凝土试件SHPB实验的波形特征分析[J].解放军理工大学学报(自然科学版), 2016, 17(04): 345-349. http://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201604007.htm [22] 潘城, 赵光明, 孟祥瑞.爆炸荷载作用下围岩累积损伤效应的数值分析[J].爆破, 2016, 33(01): 30-33+44 doi: 10.3969/j.issn.1001-8352.2016.01.007 [23] 金解放, 钟海兵, 吴越, 等.静载荷与循环冲击作用下岩石损伤变量定义方法的选择[J].有色金属科学与工程, 2013, 4(04): 85-90. http://ysjskx.paperopen.com/oa/DArticle.aspx?type=view&id=2013040015 [24] 何聪, 金解放, 周学进, 等.静载荷与循环冲击组合作用下岩石损伤本构模型研究[J].有色金属科学与工程, 2016, 7(04): 114-120. http://ysjskx.paperopen.com/oa/DArticle.aspx?type=view&id=20160420
计量
- 文章访问数: 45
- HTML全文浏览量: 28
- PDF下载量: 5
