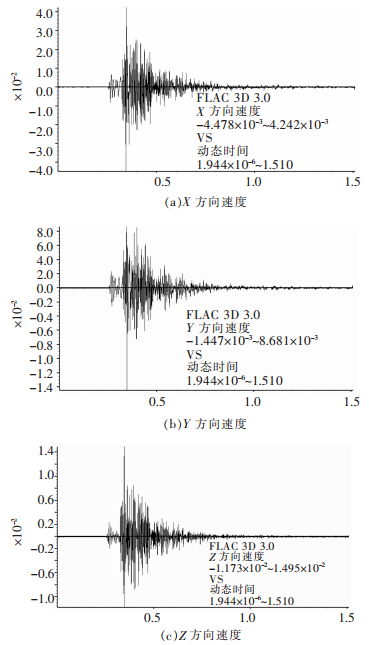
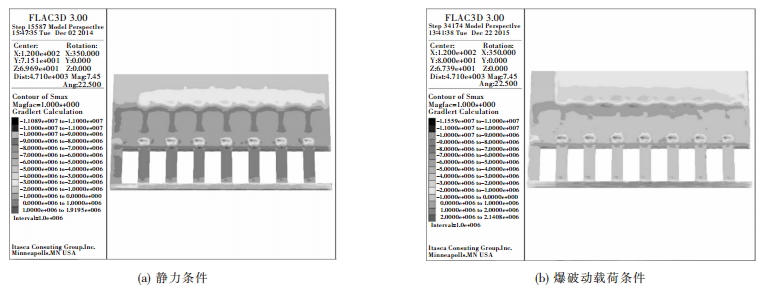
Abstract: To determine the minimum reserve safe thickness level of stage pillar, the middle stope mining from -100 m to -150 m in a copper mine in Shangrao City was studied. According to the effects of blasting vibration to practical mining, the designed stage pillar with thickness of 5 m is checked by FLAC3D. A reasonable minimum reserve safe thickness level of stage pillar is proposed. Through comparative analysis of simulation results under static and dynamic load blasting conditions, the results show that stopes are stable under static condition when the thickness of stage pillar is 5 m or 6 m. Under the blasting dynamic load condition, the stope is stable if the thickness of stage pillar is 6 m. However, when it is 5 m, the stope is in a less stable state. On the basis of analyzing theoretical model, the minimum reserve safe thickness level of stage pillars with thickness of 6 m is concluded.