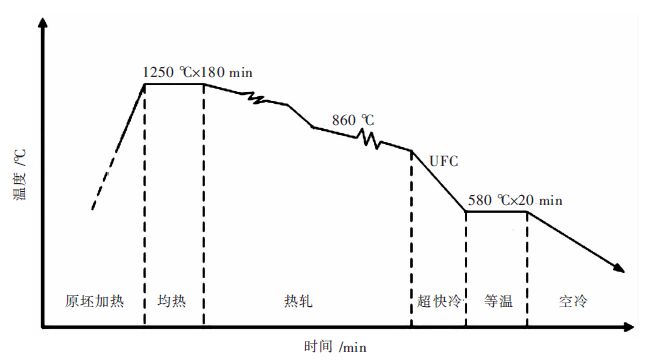
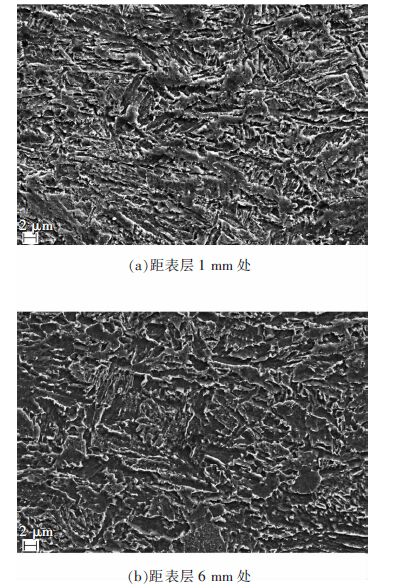
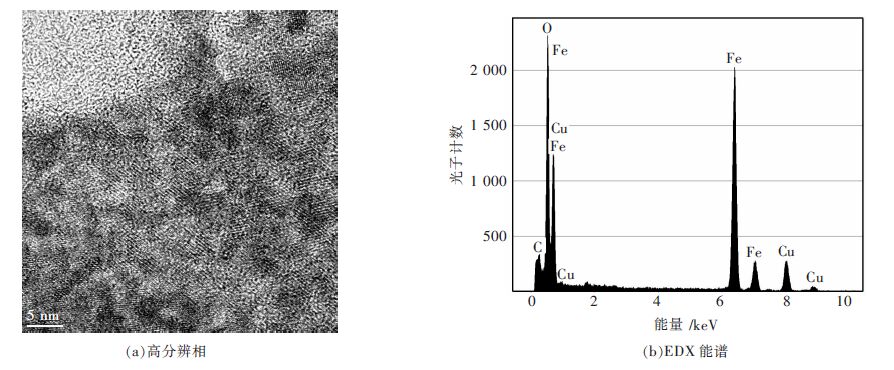
Nano-carbide precipitates in Ti microalloyed steel under ultra fast cooling condition and their strengthening effect
-
摘要: 具有较高强度的Ti微合金钢已广泛应用于国民经济及国防工业的各个领域.针对超快速冷却条件下(轧制冷却速度高达64 ℃/s)的Ti微合金钢,采用无损电解提取技术获得Ti微合金钢中的纳米碳化物. 在此基础上,运用化学相分析、X射线小角散射及透射电镜综合分析纳米碳化物的物理化学特征,并考察其强化作用. 结果表明:Ti微合金钢中存在大量纳米尺寸的FexC、TiC析出物,其平均粒度分别为76.06 nm和133.95 nm;同时,超快速冷却条件强化了FexC的析出行为,使得其析出强化增量达到243.8 MPa,而TiC的析出强化增量仅为63.1 MPa;然而,钢中每增加0.01 %(质量分数)的TiC析出物(<40 nm)却可大幅贡献强化增量77.1 MPa,远高于FexC析出物(<40 nm)的强化贡献量. 因此,强化TiC的析出行为在提高钢屈服强度方面具有重要潜力.Abstract: Ti microalloyed steel is a high strength steel and has been widely used in national economy and defense industry. The nano-carbide precipitates in the Ti microalloyed steel produced by the ultra fast cooling process with a rolling cooling rate up to 64 ℃/s were obtained by nondestructive electrolysis extraction technology, and investigated through chemical phase analysis, X-ray small angle scattering and transmission electron microscopy. In addition, its effect on steel strengthening was also discussed. The results show that a large number of nano-sized FexC and TiC precipitates exist in the Ti microalloyed steel and their average particle size are 76.06 nm and 133.95 nm, respectively. The FexC precipitation behavior is strengthened by the ultra fast cooling process. Thus, the yield strength induced by FexC precipitate reaches 243.8 MPa, while that of TiC precipitate is only 63.1 MPa. However, the increasing mass fraction of TiC precipitate (<40 nm) by 0.01 % can obviously improve the yield strength by 77.1 MPa, which is far higher than that of Fez
C precipitate (<40 nm). Therefore, strengthening the precipitation behavior of TiC plays an important role in improving steel yield strength. -
稀土素有“工业黄金”美誉, 在高新技术等新兴领域具有很大的应用价值。中国的稀土资源位于世界前列, 我国特有的南方离子型稀土矿储量、产量均位于世界第一位[1], 其大面积分布于我国江西、广东等地。江西赣州被冠于“稀土王国”之称, 坐拥全国30%以上的离子型稀土资源。正因为离子型稀土矿在各个领域的应用广泛, 加速了离子型稀土矿的开采, 然而在稀土的开采过程中伴随着严重的环境污染。目前原地浸矿依然用于离子型稀土的开采, 浸矿过程中注入大量的硫酸铵, 使得开采后的稀土矿区依然有大量的浸矿液残留, 残留的浸矿液通过地表径流、雨水冲刷和渗漏等作用污染矿区地表水体, 因而产生了大量的低碳氨氮废水, 极大地影响了稀土矿区的生态环境。
传统生物脱氮技术指出, 经过微生物的硝化和反硝化作用氨氮才能被完全去除[2-5]。其中硝化作用进行氨氧化和亚硝酸盐的氧化;反硝化作用进行硝酸盐和亚硝酸盐的还原[6-8]。短程硝化反硝化技术作为新型生物脱氮技术, 其特点在于通过控制反应条件将硝化反应控制在NO2--N大量累积的过程, 紧接着反硝化细菌经反硝化作用以NO2--N作为电子受体, 将NO2--N还原为氮气的过程[9-12]。相较于传统生物脱氮, 其优势有:仅需传统生物脱氮供氧量的75%, 反硝化反应所需的碳源(以甲醇计)仅为传统生物脱氮技术的60%;不需经过亚硝酸盐氧化为硝酸盐的过程;在硝化反应和反硝化反应阶段剩余污泥产量分别减少了33%~35%、55%[13-15];降低碱度投加量。因SBR工艺在处理低碳氮比废水上的独特优势, 已受到国内外众多学者青睐。
短程硝化反硝化技术所具备的独特优势, 促使学者们对其过程进行研究, 研究结果均表明短程硝化反硝化的难点在于难以保证NO2--N的大量积累, 各种操作因素都会对NO2--N被进一步氧化成NO3--N产生一定影响, 因此想要将短程硝化反硝化技术成熟地应用于废水处理领域, 研究将短程硝化反硝化过程稳定在大量的NO2--N积累阶段是重点[16-18]。参照近年来国内外所做一些研究[19-25], T、DO、pH、FA、SRT和有害物质等是影响短程硝化的主要因素。本实验以稀土矿区低碳氨氮废水为研究对象, 探究曝气量、碳氮比、曝气时间对短程硝化系统的影响, 优化短程硝化过程的控制条件, 对短程硝化过程的稳定运行具有参考指导意义。
1 装置与方法
1.1 实验装置
试验装置采用自制序批式活性污泥反应器(SBR);装置规格为250 mm×200 mm×260 mm, 液面至反应器顶部为20 mm, 每天定时更换进出水8 L, 通过反应器两侧阀门进行排水和排泥操作, 同时具备取样作用, 空气泵进行曝气, 曝气量由转子流量计手动调节, 反应器内置搅拌机, 起到缺氧搅拌作用的同时进行泥水混合, 恒温电热棒调节温度。装置如图 1所示。
1.2 实验方法
1.2.1 实验用水
试验初期, 自配稀土矿区低碳氨氮模拟废水进行污泥驯化, 污泥驯化完成后, 以实际废水为研究对象, 对不同操作条件下系统去除污染物的能力进行考察。稀土矿区低碳氨氮模拟废水由C6H12O6提供C源、KH2PO4提供P源、NH4Cl提供N源, 同时添加Mn2+、Co2+、Mo7+、Na+、Zn2+等离子为微生物所需微量元素[26], 试验过程中用NaHCO3调节废水pH值至8左右。实际废水水质见表 1, 自配模拟废水具体成分见表 2, 微量元素溶液组成见表 3。
表 1 废水水质主要情况(pH为无量纲)Table 1. ain conditions of wastewater quality 表 2 模拟废水组成Table 2. Table 1 Main conditions of wastewater quality
表 2 模拟废水组成Table 2. Table 1 Main conditions of wastewater quality 表 3 微量元素溶液组成Table 3. Conditions of trace element solution
表 3 微量元素溶液组成Table 3. Conditions of trace element solution
1.2.2 接种污泥驯化培养
以赣州市白塔污水处理厂二沉池污泥为试验接种污泥, 经测定生物活性很好, 并且具备良好的沉降性能。试验首先对所取活性污泥进行驯化培养, 为期25 天的全程硝化污泥培养作为污泥驯化过程第1步, 随后在此基础上, 通过将温度设置为(28±1) ℃、曝气量为65 L/h, NaHCO3调节pH至8的条件下, 经69 d的驯化周期后, 成功驯化出短程硝化反硝化污泥。
1.2.3 分析方法
NH4+-N:纳氏试剂比色法;NO2--N:N-l-萘基乙二胺比色法;NO3--N:紫外分光光度法;COD:快速消解法;DO:Metller-Told D04100型在线DO监控仪;pH采用starter3c型实验室pH计测定。
微生物多样性:采用高通量测序, DNA提取与纯化:200 g污泥样品离心15 min, 从底部沉淀物中提取DNA。二轮PCR扩增和纯化操作, PCR所用引物为Misep测序平台V3-V4通用引物341F(CCTACGGGNGGCWGCAG)和805R(GACTACHVGGGTATCAATCC)引物, 引物16S的PCR扩增条件为:95 ℃预变性30 s, 95 ℃变性10 s, 55 ℃退火20 s, 72 ℃延伸20 s, 最后完成45个循环, 将扩增产物进行电泳, 数据软件对荧光PCR数据结果进行分析。
2 结果与讨论
2.1 微生物多样性分析
驯化完成时的污泥样品送至上海生工生物工程股份有限公司进行高通量测序分析, 其中全程硝化污泥样品对应编号R0, 短程硝化污泥样品编号对应R1, 根据单样本的多样性分析结果用于评价菌群丰度以及多样性, 具体情况见表 4。
表 4 样品的生物多样性Table 4. Microbial diversity of different samples
通过OUT数值分析, 一定程度上可以反映系统中微生物菌群的丰富度, OUT数与ACE指数和Chao指数密切相关, 通常来说ACE指数和Chao指数越大, 表明其物种丰富度越高。此外, Shannon指数和Simpson指数也是评价微生物多样性的指标之一, Shannon指数与微生物多样性呈现正相关的关系;Simpson指数则相反, 其数值越大说明微生物多样性越低, 但其与优势菌种数量呈现正相关关系。
通过表 4数据可以看出, R0和R1覆盖度均高达99%, 可以认为此次测序结果能够较为全面地描述SBR系统中的微生物群落结构, 具备真实性。其中短程硝化污泥样品(R1)中的ACE指数和Chao指数相比于全程硝化污泥样品(R0)略有降低, 而Simpson指数则有所提高, 说明由全程硝化污泥驯化培养转为短程硝化污泥驯化培养过程中, 某些微生物无法适应该环境, 逐渐被淘汰, 导致微生物多样性降低。
通过在“门”和“属”水平上对系统中微生物菌种相对丰度进行分析, 以期更直观地反映不同驯化期间SBR处理稀土矿区低碳氨氮废水微生物群落结构变化情况, 分析结果如图 2、图 3所示。结果表明, 在两个不同驯化阶段, 变形菌门(Proteobacteria)、拟杆菌门(Bacteroidetes)、绿弯菌门( Chloroflexi)、放线菌门(Actinobacteria)、厚壁菌门(Firmicutes)和酸杆菌门( Acidobacteria) 等共同构成了SBR短程硝化系统中微生物群落结构组成, 其中变形菌门相对丰度达到了20.4%~42%, 拟杆菌门相对丰度达到了4%~34.5%, 逐渐成为优势菌门。
此外, 短程硝化污泥样品(R1)中被检测出浮霉菌门(Planctomycete)相对丰度为0.9%, 在全球氮循环过程中, 浮霉菌门具有一定的促进作用, 赵志瑞等[27]研究认为, 通过浮霉菌门的相对丰度可以预判系统中DO值和NH4+-N浓度, 当两者浓度处于较低水平时, 该环境适宜浮霉菌门生长繁殖。通过设定温度为(28±1)℃、曝气量为65 L/h、pH值为8的操作条件, 成功驯化出短程硝化污泥, 同时该条件下为浮霉菌门提供了良好的生存环境。硝化螺旋菌门(Nitrospirae)相对丰度为1.8%, 在有关硝化螺旋菌门的研究中发现[28-29], 归属于该门的硝化螺菌属(Nitrospira)在污水处理中起着重要作用, 是一类硝酸菌(NOB), 具有很强的硝化能力, 能够将亚硝酸盐氧化为硝酸盐。检测结果显示, 全程硝化污泥样品中NOB相对丰度为4.5%, 经过短程硝化污泥驯化过程, 短程硝化污泥样品中NOB相对丰度仅为0.5%, 说明通过设置温度为(28±1)℃、曝气量为65 L/h、pH为8的操作条件下, NOB无法适应该环境, 在竞争中逐步被淘汰。
“属”水平分析结果表明, 全程硝化污泥中norank_p_Saccharibacteria和分支杆菌(Mycobacterium)是优势菌种, 经过短程硝化驯化后, 微生物群落结构发生变化, 亚硝化单胞菌属(Nitrosomonas)相对丰度由0.05%增加至11.5%, 亚硝化单胞菌属和亚硝化螺旋菌属是一类AOB细菌, 具有很强的氨氧化能力, 然而在短程硝化污泥样品中并未检测出亚硝化螺旋菌属存在, 表明亚硝化单胞菌属逐渐成为AOB优势菌种, 而亚硝化螺旋菌属遭到淘汰, 这与污水处理中AOB以亚硝化单胞菌属广泛存在的结论相吻合[30], 从对全程硝化污泥和短程硝化污泥样品进行高通量测序结果表明, 经过驯化培养, 成功实现了系统中AOB的大量富集。
2.2 系统短程硝化性能
在成功驯化培养出短程硝化污泥后, 用实际废水进一步启动短程硝化实验, 由图 4可以看出, 实际废水并未对系统造成冲击影响, 在系统连续运行至第5 天后, 系统对NH4+-N具有良好的去除能力, 去除率始终维持在90%以上, 亚硝酸盐积累率在95%左右, 与此同时出水NH4+-N浓度稳定维持在2.07~4.01 mg/L, 此时系统具有良好的短程硝化能力。
2.3 曝气量对短程硝化过程的影响
曝气量与溶解氧浓度存在一定关系, 通过改变曝气量, 进而改变溶解氧浓度。试验通过设置不同曝气量条件, 以氮浓度变化趋势反映短程硝化进程在此过程中的变化情况。在维持其他条件不变的情况下, 于一个反应器内分别进行曝气量为90 L/h和120 L/h的单因素条件实验, 试验分别运行了15 d, 运行工况如下:进水15 min→好氧曝气300 min以内→静置沉淀1 h→排水15 min→周期循环。
图 5所列数据可以发现, 在曝气量为90 L/h条件下, 系统运行至第7 天时, 此时可认为系统已处于稳定运行状态, 对该运行状态下的系统短程硝化性能进行考察, 结果表明210 min为转折点, 反应至210 min的过程中系统内NO2--N浓度持续上升, 此后NO2--N浓度开始下降, 取而代之的是NO3--N浓度开始升高;实验进行到第8 天时, 考察曝气量为120 L/h时系统短程硝化进程, 转折点较90 L/h时提前出现, 在180 min时NO2--N浓度达到最大值。并且可以发现两种不同曝气量运行期间, 曝气量更大时, NO2--N浓度增长速率更快, 由此可以得出短程硝化进程的加快可以通过在一定范围内提高曝气量来实现。180 min后NO2--N浓度和NO3--N浓度呈现与90 L/h曝气量时相同变化趋势。
综上所述, 曝气量是SBR短程硝化过程稳定实现的重要影响因素, 为此通过固定其他因素不变, 在90、120 L/h曝气量条件下系统各运行7天, 深入研究曝气量在其中所产生的影响。由图 6实验结果可知, 90 L/h曝气量条件下, 系统内NO2--N积累率随运行时间增加呈现缓慢上升趋势, 并且始终维持在较高水平, 硝化类型为短程硝化;实验至第8 天将曝气量调至120 L/h, 第8天至第11天系统内NO2--N积累率呈现缓慢下降趋势;系统运行至第14天, NO2--N积累率降至82%, 说明过高的曝气量会破坏短程硝化系统的稳定性, 系统内硝化类型发生转变。因此, 想要获得稳定的短程硝化过程, 曝气量的严格控制是重要举措之一。
2.4 C/N对短程硝化的影响
试验考察了在不同C/N(浓度比, C/N=5、5.6、7.4)条件下, 系统短程硝化过程变化情况, 在此基础上考察了短程硝化进程在持续的高C/N的环境下的变化情况, 具体运行工况见表 5。
表 5 不同C/N系统运行工况Table 5. System operating conditions under different C/N
图 7所示数据显示, 3种不同C/N条件下, 系统内NO2--N积累率均呈现出相同变化趋势。运行条件为C/N=3.5、C/N=5.6和C/N=7.4时, 三者对应的NO2--N积累率最高值分别为97.37%、98.07%和当98.15%, 随着反应的进行, NO2--N积累率达到最高值后均开始下降, 相比于其他两种C/N条件, 当C/N=7.4时, 最先出现NO2--N积累率的下降过程。分析反应后期NO2--N积累率降低的原因可能是:一是由于反应器存在曝气盲区, 存在一定空间的缺氧区域, 缺氧环境下有利于反硝化进行, 导致NO2--N浓度下降;二是由于持续的曝气使部分NO2--N被氧化成NO3--N, 但总体而言系统仍处于较低DO环境下, 在此环境下NO2--N被氧化成 NO3--N的量非常有限, 因此仍能获得NO2--N的大量积累。至反应结束时, 3种C/N下系统NO2--N积累率仍维持在较高水平, 分析认为C/N不是影响NO2--N积累的影响因素。由图 8可知, 继续让系统在高C/N(C/N=7.4)环境下运行15 d, NO2--N积累率随时间而下降。分析其原因是可能由于反应初期, 底物充足, 加快了异养菌降解氨氮过程, 同时在曝气时间不变情况下导致DO值过高, NOB受到抑制, NO2--N积累率出现下降
2.5 固定曝气时间对短程硝化的影响
文献[31]表明, 短程硝化过程可以通过人为的实时控制实现, 本节考察了固定曝气时长对短程硝化过程的影响, 通过时间继电器固定控制曝气时长, 结合前文, 为保证硝化反应进行完全, 将曝气时长设置为330 min, 其余操作条件不变, 系统连续运行8 d, 结果如图 9。
根据图 9可以看出, NO2--N浓度变化呈现下降趋势, NO3--N浓度变化则相反, 并且前4 天 NO2--N浓度下降趋势和NO3--N浓度上升趋势并不明显, 第5 天后NO2--N浓度加速下降, NO3--N浓度大幅升高。直至第8 天时NO2--N积累率仅为48.89%, 表明此时系统短程硝化性能受到抑制。依照此趋势可以预见, 系统持续在330 min的曝气时长条件下运行, 短程硝化过程将被全程硝化所取代。分析认为, 反应初期在溶解氧充足的条件下, 系统中存在小部分NOB充分利用多余的DO, 该环境适于NOB的生长, NO2--N作为短程硝化反应的产物, 在NOB的作用下逐渐向NO3--N转化。通过实时控制曝气时长来保证短程硝化过程稳定运行, 在此过程中不仅能获得NO2--N的大量积累, 成本的节约也是经济效益的体现。
3 结 论
1)在用模拟废水对活性污泥进行驯化培养后, 以实际稀土矿区低碳氨氮废水为研究对象, 考察了系统短程硝化反硝化性能, 结果表明:实际废水未对系统造成冲击影响, NH4+-N去除率仍可达90%以上, 亚硝酸盐积累率在95%左右, 出水NH4+-N浓度稳定维持在2.07~4.01 mg/L。
2)短时间内系统短程硝化过程的稳定性不受曝气量提高的影响。90 L/h的曝气量条件下, 系统在仍具有较好的短程硝化性能;曝气量提高至120 L/h, NO2--N的积累率降至82%左右, 全程硝化逐渐取代短程硝化, 硝化类型发生转化
3)当C/N在3.5~7.4时, 系统内NO2--N积累率仍处于较高水平, 提高C/N在短时间内不会对短程硝化过程产生明显影响。但长时间的高C/N环境会使系统内NO2--N积累率降低, 一定程度上破坏了短程硝化稳定性和污泥性能。短程硝化反硝化过程在低C/N环境下更加稳定。
4)曝气时长会影响短程硝化过程, 系统中多余的DO被NOB利用, NOB生长迅速, 短程硝化逐渐被全程硝化取代。通过实时控制曝气时长有助于短程硝化过程的稳定, 在一定程度上也能达到节约成本的目的。
-
表 1 Ti 微合金钢的化学成分/(质量分数袁%)
Table 1 Chemical composition of Ti microalloyed steel /(mass fraction, %)
元素 C Mn Si P S Ti Al N* O* 含量 0.15 0.98 0.28 0.015 0.005 0.08 0.02 4~5 4~5 注:标有"*"的单位为10-5. 表 2 超快速冷却条件下Ti 微合金钢的力学性能
Table 2 Mechanical properties of Ti microalloyed steel produced by ultra fast cooling process
屈服强度/MPa 抗拉强度/MPa 屈强比 伸长率/% 650 750 0.87 17.4 表 3 析出相结构参数
Table 3 Structural parameters of precipitates
相类型 点阵常数/nm 晶系 M3C a0=0.452 3~0.453 0, b0=0.508 8~0.508 0,
b0=0.674 3~0.677 2正交 M(C,N) a0=0.425~0.427 面心立方 表 4 M3C 及MC 中各元素占钢的质量分数
Table 4 Element mass fraction of M3C and MC in steel
相结构 各元素占钢的质量分数/% 相占钢的
质量分数/%(Fe0.984Mn0.016)3C Fe Mn C ∑ 1.428 2 0.023 0 0.104 1 1.555 3 Ti(C0.672N0.328) Ti C N 0.026 7 0.004 5 0.002 6 0.033 8 表 5 M3C 及MC 类析出物的粒度分布
Table 5 Size distribution of M3C and MC precipitates
粒度/nm M3C MC 频率/(%·nm-1) 质量分数/% 累计质量分数/% 频率/(%·nm-1) 质量分数/% 累计质量分数/% 1 ~ 5 1.83 7.31 7.31 2.81 11.23 11.23 5 ~ 10 0.04 0.22 7.53 0.97 4.84 16.07 10 ~ 18 0.02 0.12 7.66 0.26 2.05 18.13 18 ~ 36 0.77 13.88 21.54 0.34 6.09 2 4.22 36 ~ 60 1.12 26.96 48.5 0.16 3.73 27.95 60 ~ 96 0.77 27.56 76.06 0.29 10.6 38.55 96 ~ 140 0.3 13.41 89.47 0.2 8.82 47.37 140 ~ 200 0.09 5.66 95.13 0.43 25.91 73.28 200 ~ 300 0.05 4.87 100 0.27 26.72 100 表 6 不同粒度纳米碳化物对析出强化的贡献
Table 6 Contribution of different sizes of nano-carbide precipitate to yield strength
粒度/nm FexC 析出强化增量/MPa 1 ~ 5 153.9 38 5 ~ 10 34.2 13.6 10 ~ 18 7.4 5.6 18 ~ 36 48.3 5.9 合计 243.8 63.1 表 7 钢屈服强度计算值与实测值的比较/MPa
Table 7 Comparison of steel yield strength between calculation and measurement /MPa
细晶强化增量 固溶强化增量 析出强化增量 理论计算值 实测值 235.3~268.3 79.7 306.9 621.9~654.9 650 -
[1] FU J, LI G, MAO X, et al. Nanoscale cementite precipitates and comprehensive strengthening mechanism of steel[J]. Metallurgical and Materials Transactions A, 2011, 42(12): 3797-3812. doi: 10.1007/s11661-011-0767-z
[2] SHIGA C, HIRAOKA K. Development of high-strength steel in STX-21 project and associated tasks[J]. Welding Technique, 1998 (7): 81-87.
[3] 傅杰, 李光强, 于月光, 等. 基于纳米铁碳析出物的钢综合强化机理[J]. 中国工程科学, 2011, 13(1): 31-42. http://www.cnki.com.cn/Article/CJFDTOTAL-GCKX201101006.htm [4] CHARLEUX M, POOLE W J, MILITZER M, et al. Precipitation behavior and its effect on strengthening of an HSLA-Nb/Ti steel[J]. Metallurgical and Materials Transactions A, 2001, 32(7): 1635-1647. doi: 10.1007/s11661-001-0142-6
[5] 付俊岩. Nb微合金化和含铌钢的发展及技术进步[J]. 钢铁, 2006, 40(8): 1-6. http://www.cnki.com.cn/Article/CJFDTOTAL-GANT200508000.htm [6] 雍岐龙, 吴宝榕, 白埃民, 等. 铌微合金钢中碳氮化铌化学组成的计算与分析[J]. 钢铁研究学报, 1990, 2(2): 37-42. http://www.cnki.com.cn/Article/CJFDTOTAL-IRON199002009.htm [7] CHEN C Y, YEN H W, KAO F H, et al. Precipitation hardening of high-strength low-alloy steels by nanometer-sized carbides[J]. Materials Science and Engineering: A, 2009, 499(1): 162-166. http://cn.bing.com/academic/profile?id=2019290790&encoded=0&v=paper_preview&mkt=zh-cn
[8] JANG J H, LEE C H, HEO Y U, et al. Stability of (Ti, M) C (M=Nb, V, Mo and W) carbide in steels using first-principles calculations[J]. Acta Materialia, 2012, 60(1): 208-217. doi: 10.1016/j.actamat.2011.09.051
[9] SETO K, FUNAKAWA Y, KANEKO S. Hot rolled high strength steels for suspension and chassis parts “NANOHITEN” and “BHT Steel”[J]. JFE Technical Report, 2007(10): 19-25. http://cn.bing.com/academic/profile?id=2305011633&encoded=0&v=paper_preview&mkt=zh-cn
[10] 李冬玲, 方建锋, 刘庆斌, 等. X-射线小角散射法测定钢铁及合金中析出相的粒度[J]. 冶金分析, 2008, 28(3): 1-8. [11] 霍向东, 毛新平, 吕盛夏, 等. CSP 生产 Ti 微合金化高强钢中纳米碳化物[J]. 北京科技大学学报, 2011, 33(8): 941-946. http://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201108007.htm [12] 吴华杰, 傅杰, 刘阳春. 微合金高强度钢纳米级析出相的分析[J]. 特殊钢, 2006, 27(4): 19-21. http://www.cnki.com.cn/Article/CJFDTOTAL-TSGA200604007.htm [13] GLADMAN T. Second phase particle distribution and secondary recrystallisation[J]. Scripta Metallurgica et Materialia, 1992, 27(11): 1569-1573. doi: 10.1016/0956-716X(92)90146-6
[14] 雍岐龙.钢铁材料中的第二相[M]. 北京: 冶金工业出版社, 2006. [15] PICKING F B, 刘嘉禾. 钢的组织与性能[M]. 北京: 科学出版社, 1999. [16] TAKAKI S. Relation between yield strength and microstructural factors-On the additional law of strengthening mechanisms[J]. Tetsu to Hagane-Journal of the Iron and Steel Institute of Japan, 2008, 94(5): A304-A309.
[17] DUTTA B, Sellars C M. Strengthening of austenite by niobium during hot rolling of microalloyed steel[J]. Materials Science and Technology, 1986, 2(2): 146-153. doi: 10.1179/mst.1986.2.2.146




 下载:
下载: