某矿井下浅孔毫秒延时爆破地表震动的数值模拟研究

吴贤振; 尹丽冰; 胡维; 高祥; 王亮亮

doi:10.13264/j.cnki.ysjskx.2014.06.017

某矿井下浅孔毫秒延时爆破地表震动的数值模拟研究

江西理工大学资源与环境工程学院，江西赣州 341000

基金项目:

江西省教育厅科技计划项目 GJJ12336

江西省研究生创新基金项目 YC2013-S185

详细信息

作者简介:
吴贤振(1971-)，男，博士，教授，主要从事爆破振动及声发射等方向的研究，E-mail：736145095@qq.com

中图分类号: TD235.46
计量
- 文章访问数: 54
- HTML全文浏览量: 31
- PDF下载量: 1
出版历程
- 收稿日期: 2014-06-24
- 发布日期: 2014-12-30
- 刊出日期: 2014-12-19

Vibration intensity of multi milliseconds blasting in underground mine based on LS-DYNA

School of Resource and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China

摘要

摘要: 某地下矿山上方地表分布有土坯房，一层、二层砖混结构民房以及水稻田.该矿山生产过程中产生的爆破震动易影响周边民房的稳定.为研究该矿山井下生产爆破时地表的震动强度，确保民房震动强度安全，利用LS-DYNA有限元方法对某次具有代表性的生产爆破下的地表震动强度进行了分析研究.通过对该次具有代表性的生产爆破数值计算与爆破震动现场测试结果对比分析表明，采用ANSYS/LS-DYNA的数值计算结果与实际测试值偏差不大，数值模拟分析方法对爆破震动强度的预测具有一定的指导价值.
- ANSYS/LS-DYNA /
- 多段毫秒延时爆破 /
- 爆破震动
Abstract: There are adobe houses, one or two layers of brick housing and paddy field over the underground mine. The stability of the houses is influenced by blasting vibration generated during the production process of the mines. In order to predict vibration intensity and ensure the safety of surface buildings in an underground mine production multi millisecond blasting, a numerical simulation analysis of the vibration of a certain representative production blasting is conducted by LS-DYNA software. The comparative analysis of the numerical results and the actual measurements shows that the result of ANSYS/LS-DYNA software element software has little difference with the actual test values. ANSYS/LS-DYNA software has a certain guiding value to forecast blasting vibration intensity.
- ANSYS/LS-DYNA /
- multi milliseconds blasting /
- blasting vibration

HTML全文

随着铜冶炼技术的发展,传统的熔炼方法逐渐被现代高效、节能、低污染的闪速和熔池熔炼方法所取代^[1]。强化熔炼过程产生的炉渣含铜量很高,铜的损失率达3.8%^[2-3]。铜渣的输运性质（特别是黏度）是决定渣中铜损失的关键因素^[4]。黏度是影响炉渣性能的重要物理性质。炉渣的黏度受化学成分和温度的影响很大。此外,黏度也是优化和改进各种冶金操作所需矿渣的关键性能。因此,有必要对铜渣的黏度进行研究,为提高铜锍和炉渣的分离效率,降低铜冶炼过程中铜的损失奠定基础。

近年来,国内外研究者对铜冶炼渣黏度展开研究。SANTHY等^[5]研究了氧硅比和温度对CaO-FeO-SiO₂黏度的影响,通过经验参数来预测黏度。研究结果表明：黏度随氧硅比的增加或温度的升高而降低。HOU等^[6]采用空气气氛下的旋转法测量黏度,并利用拉曼光谱和傅里叶变换红外光谱（FTIR）研究了熔渣的微观结构演变。研究结果表明：当Cr₂O₃含量在0~5%时,铜转炉渣黏度从0.464 Pa·s增加到8.000 Pa·s。此外,还揭示了Cr₂O₃对铜转炉炉渣黏度和微观组织的影响机理。SHIRAISHI等^[7]利用旋转圆筒法测量了在1 250 ~ 1 450 ℃温度范围内,SiO₂含量在0~38%范围内（质量分数,下同）的FeO-SiO₂熔体黏度。结果表明：随着温度的升高,Fe-SiO₂的黏度逐渐降低,随着SiO₂含量的增加,Fe-SiO₂的黏度逐渐升高。CHEN等^[8]测量了FeO-SiO₂体系在1 200~1 500 ℃时的黏度,并与Factsage黏度模型、准化学黏度（QCV）模型和修正后的准化学黏度模型的计算结果进行了对比。结果表明：修正后的QCV模型和Factsage模型的计算结果与实验数据较为吻合,而QCV模型在SiO₂浓度较高时黏度计算偏差较大。ZHANG等^[9]利用旋转法测量了FeO_t-SiO₂-CaO熔渣的黏度,发现随着CaO的加入,富铁熔渣的黏度先减小后增大。ZHANG等^[10]研究表明随着CaO含量的增加,铜冶炼渣的黏度逐渐降低,直至析出固相,黏度迅速增大。PARK等^[11]采用转轴法对FeO-SiO₂-Al₂O₃铜渣进行分析,结果表明：其黏度随Fe/SiO₂比值的增加而降低。苏凤来等^[12]发现铜冶炼渣的黏度随着碱度的增加先增大后减小,随着FeO的加入而减小。徐翔等^[13]研究了CaO、Al₂O₃和Cu₂O添加剂对铜冶炼渣黏度的影响,铜渣的黏度随CaO含量的增加先降低后升高,加入Al₂O₃和Cu₂O会导致黏度升高。

铜渣黏度测量领域虽然取得了一些成果,但仍存在一些不足。一方面,高温下铜渣黏度测量存在不确定性；另一方面,对铜渣黏度变化的本质原因缺乏更深入的认识。铜渣的黏度变化间接反映了其结构变化,为了揭示铜渣黏度变化的根本原因,有必要对铜渣的结构进行研究。

分子动力学（Molecular Dynamics, MD）模拟不仅可以观察到原子在物理化学过程中的微观细节,还可以提供通过实验无法获得或难以获得的重要信息^[14]。目前,MD模拟已成功地应用于冶金渣的结构研究,构建沟通炉渣微观和宏观性质的桥梁^[15]。考虑到铜渣中FeO和SiO₂占成分90%以上,本文选择FeO-SiO₂体系代表铜渣作为模拟对象。通过MD模拟,得到了FeO-SiO₂体系的径向分布函数（RDF）、配位数（CN）函数、键角分布、氧连接状态、自扩散系数及黏度,据此研究了FeO-SiO₂体系的结构。本文的研究结果将为降低铜锍冶炼过程中铜的损失,实现铜资源的高效利用提供理论指导。

1 模拟方法

1.1 势函数和参数

采用Buckingham势函数对铜渣的结构进行研究,其表达式如式（1）所示。原子间的相互作用用长程势（库仑项）和短程势（Buckingham项）的组合来描述。

V (r_{i j}) = \frac{Z_{i} Z_{j} e^{2}}{4 π ε_{0} r_{i j}} + A_{i j} e x p (\frac{- r_{i j}}{ρ_{i j}}) - \frac{C_{i j}}{{r_{i j}}^{6}}

(1)

式（1）中：V（r_ij）为原子i和j间的总势能；ε₀为介电常数,其值为8.85×10^-12 C²N^-1m^-2；r_ij为原子i和j之间的距离,单位Å；A_ij、ρ_ij和C_ij为经验参数；Z_i和Z_j为原子i和原子j的有效电荷,单位为eV。Fe、Si、O原子的有效电荷分别为1.2、2.4、-1.2 eV。最初的Buckingham势存在一个问题,即当2个原子相互靠近时,会导致体系结构异常。为了避免该问题,当原子i和j之间的距离小于r_s时,采用式（2）函数形式代替式（1）中的Buckingham项。

V' (r_{i j}) = B_{i j} r_{i j}^{2} + D_{i j} r_{i j}^{n}

(2)

式（2）中：B_ij、D_ij和n参数是为了保证势能、相互作用力在原子对势能曲线r_s处的连续。本研究所用的势参数列于表1^[16-17]。O-O、O-Si和O-Fe原子对的r_s分别为1.906、1.168 Å和0.917 Å。

表 1 Buckingham势参数

Table 1. Buckingham potential parameters

原子i	原子j	A_ij/eV	ρ_ij/Å	C_ij/（eV·Å⁶）	B_ij/（eV·Åⁿ）	D_ij/（eV·Å²）	n
O	O	2 029.220	0.343 645	192.58	46.462	-0.326	3.430
O	Si	13 702.905	0.193 817	54.68	28.942	-3.025	3.949
O	Fe	11 777.070	0.207 132	21.64	104.203	-32.110	2.670

下载: 导出CSV

| 显示表格

1.2 模拟条件及过程

本文采用LAMMPS软件进行MD模拟,采用随机初始构型和周期边界条件。本次MD模拟过程原子总数设置为6 000,采用NVT系综。采用蛙跳算法求解原子牛顿运动方程,每10步保存数据。将势能相互作用的截断半径设置为10 Å,模拟的时间步长设置为1 fs。模拟样品的组成、原子数量、盒子边长和密度列于表2。

表 2 模拟样品的成分、原子数、盒子边长和密度

Table 2. Composition, atomic number, cubic length, and density of simulated sample

样品	成分/%		原子数/个				盒子边长/Å	密度/（g/cm³）
样品	FeO	SiO₂	Fe	Si	O	总数	盒子边长/Å	密度/（g/cm³）
1	85	15	2 280	480	3 240	6 000	42.91	4.05
2	80	20	2 070	620	3 310	6 000	42.83	3.93
3	75	25	1 896	736	3 368	6 000	42.77	3.83
4	70	30	1 695	870	3 435	6 000	42.71	3.71
5	65	35	1 527	982	3 491	6 000	42.77	3.58
6	60	40	1 365	1090	3 545	6 000	42.82	3.46
7	55	45	1 215	1190	3 595	6 000	42.86	3.35
8	50	50	1 074	1284	3 642	6 000	42.97	3.23

下载: 导出CSV

| 显示表格

FeO-SiO₂体系将按照以下步骤进行模拟：首先,将所有原子随机放入盒子中,盒子的大小由摩尔质量和密度决定。系统初始温度设置为5 000 K,保持1 000 ps以完全消除初始构型的记忆。其次,在2 000 ps内以一定的冷却速率从5 000 K降温到1 673 K。然后,待系统达到平衡状态后,将体系在1 673 K下再保持1 000 ps,获得空间坐标,分析FeO-SiO₂体系的结构。

1.3 结构信息

RDF的定义是在与某个原子距离为r到∆r之间的原子的平均数。RDF是表征熔体或非晶固体结构最重要的函数。RDF可以表示原子的分布特征,也可以表示系统中结构与整体结构的区别。原子间的CN和键长可以直接从RDF中得到,前者是对RDF进行积分得到的,后者是RDF第一个峰位置的横坐标值。RDF和配位数CN的定义如式（3）和式（4）所示。

g (r) = \frac{V}{N_{i} N_{j}} \sum_{j} \frac{n (r)}{4 π r^{2} ∆ r}

(3)

C N (r) = \frac{4 π N_{j}}{V} \int_{0}^{r} r^{2} g (r) d r

(4)

式（3）、式（4）中：N_i和N_j分别为原子i和原子j的总个数；V为体系的总体积,单位Å³；n（r）表示以某个原子i为中心,在与其距离为r到∆r之间的原子j的平均数量,距离r的单位为Å。

1.4 输运性质

输运过程是指一种非平衡过程,扩散和黏度是描述熔体输运性质中的2个重要参数,分别对应质量和动量运输。均方位移（MSD）是指在任意时刻所有原子距离各自初始点的距离的平均值,其表达式如式（5）所示。自扩散系数（D）代表原子的扩散能力,可通过式（6）得到。在此基础上,黏度（η）可通过Einstein-Stokes方程导出。

M S D = \frac{1}{N} （ \sum_{1}^{N} | r (t) - r (0) |^{2} ）

(5)

D = \underset{t \to \infty}{l i m} \frac{d [∆ \bar{r} {(t)}^{2}]}{d t}

(6)

η = \frac{k T}{λ D}

(7)

式（5）—式（7）中：r_i（t）为原子i在t时刻的坐标,r_i（0）为原子i在0时刻的坐标,单位Å；k为玻尔兹曼常数,单位J/K；T为熔体温度,单位K。λ是扩散离子的平均扩散距离,对于冶金熔体体系,λ一般取O^2-的直径（即λ=2R（O²）=2.8 Å）^[18-19]。

2 结果与讨论

2.1 径向分布函数

利用RDF曲线可以获得熔体结构的基本信息。RDF曲线上第一个峰的横坐标值对应平均键长或原子距离,第一个谷的横坐标值对应相应原子对的截止半径。FeO-SiO₂体系（样品4）中原子对的RDF如图1所示。由图1可知,Si-O和Fe-O的平均键长分别为1.60 Å和2.07 Å,Si-O和Fe-O的截止半径分别为2.30 Å和3.00 Å。O-O、Si-Si、Fe-Fe和Fe-Si的平均原子距离分别为2.62、3.14、3.22、3.34 Å。

图 1 FeO-SiO₂体系的RDF（样品4）

Figure 1. RDFs of FeO-SiO₂ system （sample 4）

下载: 全尺寸图片幻灯片

本研究的平均键长和原子距离与文献[20-30]的比较列于表3。从表3可以看出,本次模拟获得的平均键长和原子距离与文献中的模拟结果比较符合。

表 3 本研究与文献中的键长比较

Table 3. Comparison of bond lengths in this work and the literature

键长/Å						参考文献
Si-O	Fe-O	O-O	Si-Si	Fe-Fe	Fe-Si	参考文献
1.62	2.02	2.65	—	—	3.25	[20]
1.61	2.06	2.64	3.19	—	—	[21]
1.60	1.90	2.65	3.20	3.20	—	[22]
1.61	2.05	—	—	—	—	[23]
1.61	2.04	2.70	—	—	—	[24]
1.62	2.06	—	—	—	—	[25-26]
1.62	2.04	2.60	3.14	3.29	3.31	[27]
1.62	2.06	—	3.17	—	—	[28-29]
1.62	2.07	2.60	3.18	—	—	[30]
1.60	2.07	2.62	3.14	3.22	3.34	本文
注：“—”指未作统计。

下载: 导出CSV

| 显示表格

不同FeO含量的重要原子对的RDF如图2所示。由图2可以看出,Si-O的平均键长基本保持不变,为1.60 Å。随着FeO含量从50%增加到85%,Fe-O的平均键长从2.08 Å缩短到2.07 Å；Si-Si的平均原子距离从3.14 Å缩短到3.13 Å；O-O的平均原子距离从2.64 Å缩短到2.62 Å。键长长度的变化与相应的键能有关,由此可知,Si-O的键能大于Fe-O键能。

图 2 不同FeO含量原子对的RDF：（a） Si-O；（b） Fe-O；（c） Si-Si；（d） O-O

Figure 2. RDFs of atomic pairs with different FeO contents：（a） Si-O；（b） Fe-O；（c） Si-Si；（d） O-O

下载: 全尺寸图片幻灯片

2.2 配位数

CN是表征熔体结构基本信息的另一个重要参数。CN可以用来确定熔体中主要结构单元的几何构型。熔体的结构“远程无序和近程有序”清晰地反映在CN函数曲线上。FeO-SiO₂体系（样品4）中原子对的CN如图3所示。

图 3 FeO-SiO₂体系CN（样品4）

Figure 3. CN of FeO-SiO₂ system （sample 4）

下载: 全尺寸图片幻灯片

从图3可以看出,Si-O的CN曲线只有一个稳定的平台。这一现象表明[SiO_n]多面体是FeO-SiO₂体系中一种稳定的结构单元。从Si-O的CN曲线可以看出,平均CN（Si-O）为4.02。这一现象表明[SiO₄]^4-四面体可能是所有[SiO_n]多面体中的主要结构单元。随着FeO含量的变化,CN（Si-O）只有微小变化,表明[SiO₄]^4-四面体具有较高的结构稳定性。

2.3 键角分布

通过键角分布可以推测其几何构型和连接状态,并且能识别[SiO_n]多面体的几何构型。通过O-Si-O的键角分布可以识别[SiO_n]多面体之间的连接状态。不同FeO含量O-Si-O的键角分布如图4所示。由图4可以看出,当FeO含量从85%下降到50%时,O-Si-O键角保持在108.00°不变。108.00°的O-Si-O键角接近于理想四面体角109.48°,与其他研究的O-Si-O键角一致^[31]。O-Si-O键角没有变化,表明[SiO₄]^4-四面体具有较高的结构稳定性。

图 4 不同FeO含量O-Si-O的键角分布

Figure 4. Bond angle distributions of O-Si-O with different FeO contents

下载: 全尺寸图片幻灯片

不同FeO含量Si-O-Si的键角分布如图5所示。从图5可以看出,随着FeO含量从85%下降到50%时,Si-O-Si键角从140.00°增加到144.98°。Si-O-Si键角与其他研究中的Si-O-Si键角一致^[32-33]。

图 5 不同FeO含量Si-O-Si的键角分布

Figure 5. Bond angle distributions of Si-O-Si with different FeO contents

下载: 全尺寸图片幻灯片

此外,Si-O-Si键角的明显变化表明：随着FeO含量的变化,[SiO₄]^4-四面体在空间中的相对位置会发生变化。Si-O-Si键角分布曲线上只有唯一的峰,表明：[SiO₄]^4-四面体之间只有一种连接方式（即[SiO₄]^4-四面体之间通过共顶角来连接）。每个[SiO₄]^4-四面体中Si⁴⁺的静电势非常大,相邻Si⁴⁺之间存在很强的斥力。[SiO₄]^4-四面体之间只通过顶点而不是边或面连接,相邻Si⁴⁺之间才能产生最大距离和最小斥力,从而使体系中的结构稳定聚合。

2.4 氧连接

氧连接状态与体系的整体结构强度密切相关,也对体系的理化性质（如黏度）有直接影响。通常情况下,在硅酸盐熔体的结构中,氧原子分为桥氧（BO）、非桥氧（NBO）和自由氧（FO）。BO连接2个相邻的[SiO₄]^4-四面体；NBO连接一个[SiO₄]^4-四面体和一个金属阳离子；FO连接2个金属阳离子。前者提高了体系的聚合度,而后两者降低了体系的聚合度。不同FeO含量的氧连接分布如图6所示。

图 6 不同FeO含量的氧连接分布

Figure 6. Oxygen connection state with different FeO contents

下载: 全尺寸图片幻灯片

从图6可以看出,随着FeO含量从85%下降到50%,FO的比例从42.64%下降到1.74%,BO的比例从1.84%上升到42.60%,NBO的比例从52.52%增加到55.65%。不同类型氧的变化表明：随着FeO含量的降低,体系的聚合度和整体结构强度都有所提高。

Q_n是一个重要的结构参数,用于提供结构单元如何连接的信息。体系的聚合程度或复杂程度可用Q_n和NBO/T表示。n是给定结构单元中桥氧的数目。在硅酸盐熔体中,有5种不同的[SiO₄]^4-四面体。它们分别由Q₀、Q₁、Q₂、Q₃和Q₄表示,分别对应单体、二聚体、链状、层状和网状四面体。熔体的聚合程度可以用NBO/T来表示,NBO/T是每个[SiO₄]^4-四面体中的NBO的个数。NBO/T的比值越小,表明聚合度越高。不同FeO含量FeO-SiO₂体系中结构单元Q_n和NBO/T的分布如图7所示。由图7可以看出,随着FeO的含量从85%下降到50%,Q₄的比例从0上升到15.36%,Q₃的比例从0.02%上升到33.48%,Q₂的比例从2.02%上升到32.32%,Q₁的占比由20.72%下降到15.45%,Q₀的占比由77.42%下降到3.39%。NBO/T从2.42下降到0.25,NBO/T的减小表明体系的聚合度随着FeO含量的降低而明显升高。

图 7 不同FeO含量结构单元Q_n和NBO/T分布

Figure 7. Distribution of structural units Q_n and NBO/T in FeO-SiO₂ system with different FeO contents

下载: 全尺寸图片幻灯片

2.5 自扩散系数和黏度

根据MD模拟得到的MSD曲线和式（5）,可以计算出不同离子的扩散系数,如图8所示。由图8可知,各离子自扩散系数由大到小依次为D（Fe²⁺）>D（O^2-）>D（Si⁴⁺）,取值范围分别为1.89×10^-10~1.24×10^-9 m²/s、1.17×10^-11~4.89×10^-10 m²/s和6.85×10^-12~3.06×10^-10 m²/s。由于Si⁴⁺离子在体系中形成网络状结构,并且较为稳定,体系中会形成桥氧（BO）、非桥氧（NBO）和自由氧（FO）等结构,因此Si⁴⁺和O^2-的自扩散系数远小于Fe²⁺,且D（O^2-）>D（Si⁴⁺）。

图 8 不同FeO含量自扩散系数

Figure 8. Self-diffusion coefficient with different FeO content

下载: 全尺寸图片幻灯片

根据氧原子的自扩散系数,在1 673 K时通过式（7）计算了每个样品的黏度。此外,还通过Factsage软件计算黏度,计算结果如图9所示。从图9中可以看出,计算的黏度与Factsage变化趋势相同,与Rontgen测量的黏度对比较为吻合。其中,黏度与聚合度紧密相关,随着FeO含量的增加,体系中聚合度下降,黏度逐渐降低,黏度从0.74 Pa·s降低到0.02 Pa·s。从铜渣熔体黏度的模拟结果而言,当FeO含量处于50%~70%时,随着FeO含量的增加,体系黏度降低明显,而当FeO含量大于80%时,黏度变化不明显。事实上,随着FeO含量的增加（即SiO₂含量降低）,铜渣熔体的黏度下降,有利于铜渣和铜锍进行分离,降低铜损失。同时,随着铜渣SiO₂含量的降低,铜锍在铜渣中的溶解度将增加,增加铜损失。因此,在实际生产过程中,建议铜渣熔体黏度控制在合理范围,即铜渣成分控制在合理范围。对于铜的闪速熔炼而言,Fe/SiO₂一般控制在1.30左右,即FeO含量控制在63%左右。

图 9 在1 673 K下FeO-SiO₂体系的黏度

Figure 9. Viscosity of FeO-SiO₂ system at 1 673 K

下载: 全尺寸图片幻灯片

3 结论

通过MD模拟得到了FeO-SiO₂体系的径向分布函数、配位数、键角分布、氧连接分布、自扩散系数和黏度,据此研究了FeO-SiO₂体系的结构。结论如下：

1）随着FeO含量从85%下降到50%,Si-O的键长保持1.60 Å不变,Fe-O的键长从2.07 Å增长到2.08 Å。

2）随着FeO含量从85%下降到50%,O-Si-O键角保持在108.00°不变,Si-O-Si键角从140.00°增加到144.98°。

3）随着FeO含量从85%下降到50%,自由氧的比例从42.64%下降到1.74%,桥氧的比例从1.84%上升到42.60%,NBO/T从2.42下降到0.25,体系的聚合度随着FeO含量的降低而升高。

4）自扩散系数由大到小依次为D（Fe²⁺）>D（O^2-）>D（Si⁴⁺）。随着FeO含量从50%增加到85%,体系黏度从0.74 Pa·s降低到0.02 Pa·s。

5）[SiO₄]^4-四面体是FeO-SiO₂体系的主要结构单元并且其结构稳定性较好,四面体之间通过共顶角连接。

图 1 各测点地表布置示意图

下载: 全尺寸图片幻灯片

图 2 有限元模型图

下载: 全尺寸图片幻灯片

图 3 炮孔附近加密图

下载: 全尺寸图片幻灯片

图 4 数值计算中测点布置图

下载: 全尺寸图片幻灯片

图 5 各测点合速度-时间曲线

下载: 全尺寸图片幻灯片

图 6 各测点水平径向(L)速度-时间曲线

下载: 全尺寸图片幻灯片

图 7 各测点垂直方向(V)速度-时间曲线

下载: 全尺寸图片幻灯片

图 8 各测点水平切向(T)速度-时间曲线

下载: 全尺寸图片幻灯片

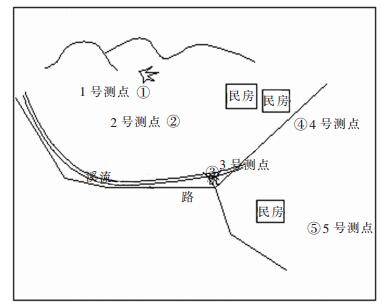
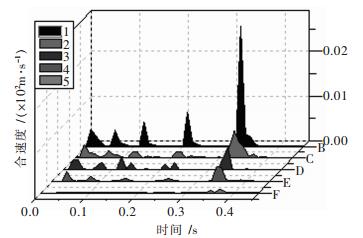
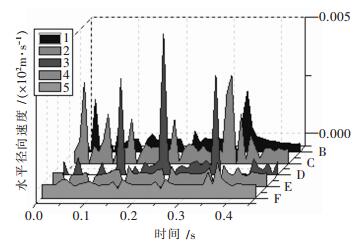
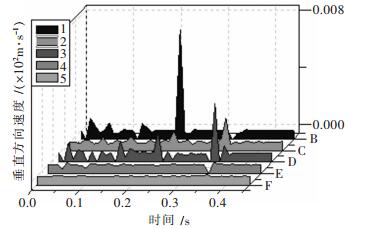
表 1 各测点实测振速峰值

测点	斜距/m	最大合成速度/(cm·s^-1)	三维方向及其对应速度/(cm·s^-1)		主震频率/Hz
测点1	84.91	1.136	T	1.11	35.5
			V	1.04	42.0
			L	9.93	15.8
测点2	171.93	0.291	T	0.190	8.63
			V	0.245	10.9
			L	0.241	9.25
测点3	258.61	0.116	T	0.063 5	10.4
			V	0.010 2	30.7
			L	0.010 2	27.3
测点4	285.31	0.282	T	0.216	27.0
			V	0.216	20.0
			L	0.279	37.0
测点5	298.40		振速小于0.051 cm/s, 没有触发测振仪

下载: 导出CSV

表 2 花岗岩主要物理力学参数表

密度/(kg·m^-3)	单轴抗压强度/MPa	泊松比	弹性模量/MPa	纵波速/(m·s^-1)
2 566	142	0.3	4.66×10⁴	4 500

下载: 导出CSV

表 3 炸药主要参数表

密度/(kg·m^-3)	爆速/(m·s^-1)	A	B	R₁	R₂
1 000	3 600	2.140×10¹¹	1.82×10⁹	4.15	0.95

下载: 导出CSV

表 4 土体主要参数表

密度/(kg·m^-3)	G	K	a₀	a₁	a₂	P_c
1.8×10³	1.601×10³	1.328×10¹⁰	3.3×10⁹	1.31×10⁴	0.123 2	0.0

下载: 导出CSV

表 5 各测点模拟计算振速峰值

测点	斜距/m	最大合成速度/(m·s^-1)	三维分速度方向	三维方向速度/(m·s^-1)
测点1	84.91	2.70	T	2.54
			V	0.861
			L	0.308
测点2	171.93	0.611	T	0.492
			V	0.264
			L	0.351
测点3	258.61	0.492	T	0.394
			V	0.346
			L	0.462
测点4	285.31	0.329	T	0.283
			V	0.301
			L	0.317
测点5	298.40	0.091	T	0.012 8
			V	0.010 7
			L	0.069

下载: 导出CSV

参考文献(15)

[1]	石少卿, 康建功, 江敏, 等.L S-DYNA在爆炸与冲击领域内的工程应用[M].北京:中国建筑工业出版社, 2011.
[2]	张智超, 刘汉龙, 陈育民, 等.爆破地震的数值模拟及爆破振动规律分析[J].郑州大学学报(工学版), 2012, 33(5):10-15. http://www.cnki.com.cn/Article/CJFDTOTAL-ZZGY201205004.htm
[3]	夏祥, 李海波, 李俊如, 等.岩体爆生裂纹的数值模拟[J].岩土力学, 2006, 27 (11): 1987-1991. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200611026.htm
[4]	梁斌, 陈忠富, 卢永刚.柱形装药在混凝土中爆炸波传播数值模拟[J].弹箭与制导学报, 2008, 28(4):93-95. http://www.cnki.com.cn/Article/CJFDTOTAL-DJZD200804027.htm
[5]	肖明, 张雨霆, 陈俊涛, 等.地下洞室开挖爆破围岩松动圈的数值分析计算[J].岩土力学, 2010, 31(8): 2613-2618. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201008044.htm
[6]	杨海书, 林从谋, 林丽群, 等.复杂结构体系下隧道爆破振动对房屋影响的试验研究[J].山东科技大学学报(自然科学版), 2011(2):65-79. http://www.cnki.com.cn/Article/CJFDTOTAL-SDKY201102010.htm
[7]	张智超, 陈育民, 刘汉龙.微差爆破模拟天然地震的数值分析与效果评价[J].岩土力学, 2013(1): 265-274. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301039.htm
[8]	李宁, 张承客, 周钟.边坡爆破开挖对邻近已有洞室影响研究[J].岩石力学与工程学报, 2012(增刊2): 3471-3476. http://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2012S2004.htm
[9]	肖文芳, 肖文涛, 房泽法.地铁隧道掘进爆破地表振动效应研究[J].工程爆破, 2012, 18(2):46-49. http://www.cnki.com.cn/Article/CJFDTOTAL-GCBP201202014.htm
[10]	史秀志, 曾志林, 田建军, 等.深井开采爆破对巷道影响的数值模拟分析[J].工程爆破, 2010, 16(2):10-14. http://www.cnki.com.cn/Article/CJFDTOTAL-GCBP201002004.htm
[11]	时党勇, 李裕春, 张胜民.基于ANSYS/LS-DYNA8.1进行显式动力分析[M].北京:清华大学出版社, 2005.
[12]	白金泽. LS-DYNA3D理论基础与实例分析[M].北京:科学出版社, 2005.
[13]	何涛. ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社, 2007.
[14]	尚晓江, 苏建宇, 魏久安, 等.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京:北京水利水电出版社, 2006.
[15]	Schneidersr. A-grid algorithm for the generation of hexahedral element meshes[J].Engineering with computers, 1996(12):168-177. doi: 10.1007/BF01198732

施引文献

资源附件(0)

图(8) / 表(5)

计量

文章访问数: 54
HTML全文浏览量: 31
PDF下载量: 1
被引次数: 0

1 模拟方法
1.1 势函数和参数
1.2 模拟条件及过程
1.3 结构信息
1.4 输运性质
2 结果与讨论
2.1 径向分布函数
2.2 配位数
2.3 键角分布
2.4 氧连接
2.5 自扩散系数和黏度
3 结论

某矿井下浅孔毫秒延时爆破地表震动的数值模拟研究

作者简介: 吴贤振(1971-)，男，博士，教授，主要从事爆破振动及声发射等方向的研究，E-mail：736145095@qq.com

计量

出版历程