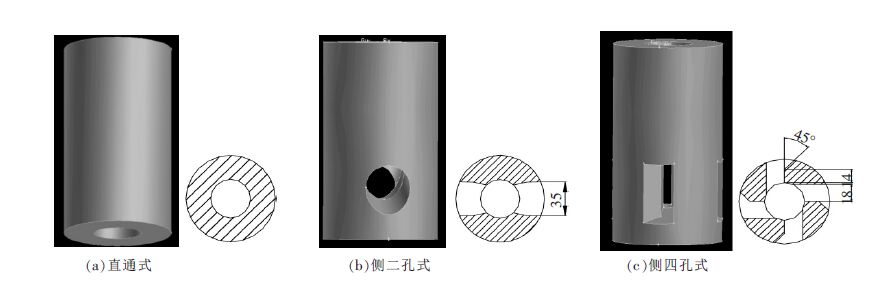
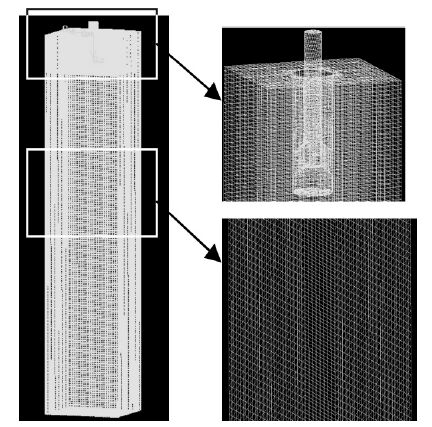
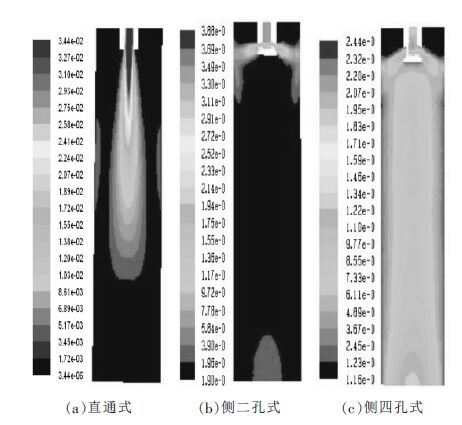
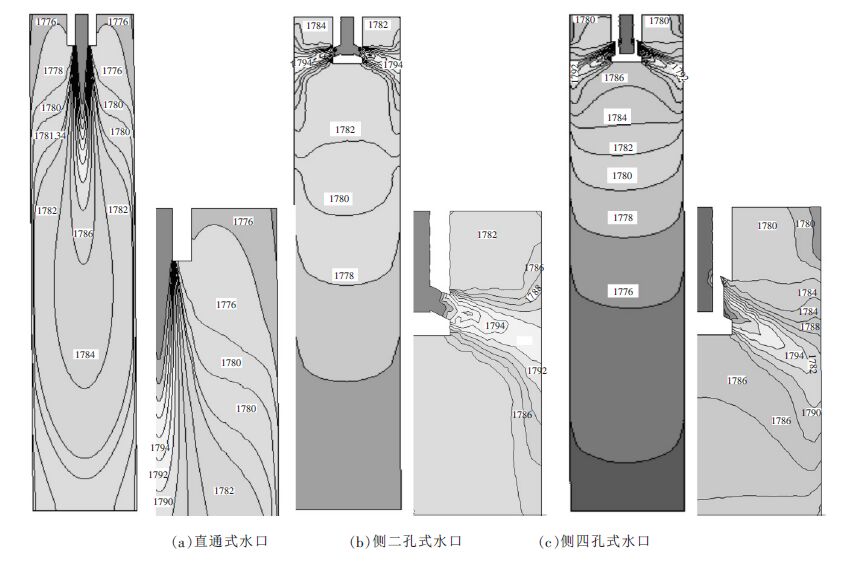
Effects of SENs types on flow patterns and temperature distribution in bloom mold
-
摘要: 利用 Fluent 流体力学软件对直通式、侧二孔式、侧四孔式浸入水口对大方坯连铸结晶器内钢水流场和温度场进行了数值模拟.结果表明,从流场来看,直通式冲击深度最大,侧二孔式次之,侧四孔式最小,侧四孔式水口在结晶器内钢水能形成上、下两个回流,其下回流涡心较直通式水口从 590 mm 上移至 270 mm,有利于夹杂物的上浮.从温度场来看,侧二孔式和侧四孔式较直通式水口使结晶器内热中心明显上移,且其弯月面钢水温度比直通式分别提高了 6 K 和 4 K,有利于保护渣的熔化.Abstract: The flow field and temperature distribution of molten steel in the bloom casting mold have been simulated under the conditions of single straight SEN, side two -furcated SEN, and side quad -furcated SEN by using hydrodynamic software fluent. Results showed that,seeing from flow field,the impingement depth of single straight SEN was the largest, that of side two-furcated SEN was larger, and the depth of side quad-furcated SEN was smallest. The upper and lower double rolls were formed in the side quad-furcated SEN mold. The vorticity of center of the lower roll changed from 590 mm to 270 mm compared with that of single straight SEN , in favor of the remove of inclusions. As seen from temperature distribution ,the thermal center moved upward obviously and center temperature of the shell increased 6 K and 4 K respectively with the side two -furcated SEN and the side quad-furcated SEN, which contributed to the melt of mold power.
-
Keywords:
- nozzle /
- mould /
- fluid flow /
- temperature distribution /
- numerical simulation
-
由于没有对陕西某钒矿其矿山的不同生产区域的初始爆破参数及时调整优化,导致爆破效果不佳,矿石块度不能满足选矿要求;在高分段,大间距的情况下前排炮孔起爆对后排炮孔破坏严重,导致后续装药困难,爆破生产效率降低;在放矿过程中凭借经验出矿,放矿管理不科学,导致放出矿石损失贫化严重[1].为了有效控制爆破成本,提高生产效率和经济效益,本文在爆破试验的基础上进行了爆破参数的优化设计.
1 工程背景和岩石特性
工程地质调查发现,矿区以砂岩、砂砾岩型矿岩为主要成分且矿化规模大,产出稳定,形成细脉状,微细浸染状矿石,矿床工业类型为砂(砾)岩型层控矿床.矿区矿体的节理发育多为钙质、多具团块状构造,工程地质特性复杂多变,结构较不完整,矿体具有碎裂岩体的特征,稳定性差.顶底板岩性复杂,主要以青石化白云岩和粗砂岩主,这类岩石在风化和外界扰动的情况下易软化,导致抗压强度较低,稳定性较差.
2 爆破漏斗试验
标准爆破漏斗实验选用YGZ-90型凿岩机打孔,钻头的孔径是60 mm,在巷道内垂直向上打扇形炮孔,初始炮孔间排距1.5 m.矿山炸药是粉状铵油炸药,装药直径为65 mm,炸药的密度为0.98 g/cm3,采用导爆管雷管起爆,试验具体方案见表 1.
表 1 爆破的试验数据炮孔序号 装药量/kg 堵塞长度/m 漏斗半径/m 设计抵抗线/m 实测抵抗线/m 爆破效果 1 0.75 0.7 0.81 0.62 0.65 均匀块度 2 0.75 0.7 0.86 0.62 0.63 均匀块度 3 0.75 0.7 0.84 0.62 未测到 冲泡 4 0.75 0.7 0.85 0.62 0.61 均匀块度 5 0.75 0.7 0.71 0.62 0.53 大块、碎块多 6 0.75 0.7 1.03 0.62 0.71 大块多 对爆破完成后炮孔,取8个不同方向的平均值作为漏斗半径和实测最小抵抗线[2],从表 1经过剔除后求得爆破漏斗半径的平均值为0.84 m,最小抵抗线的平均值为0.62 m,实际的爆破漏斗n值为1.35,最初选择的炸药q为1.84 kg/m3,根据鲍列斯阔夫公式Q=(0.4+0.6n3)qW3,化简可得到式(1)校正初选炸药单耗[3].
$$q = q'/\left( {0.4 + 0.6{n^3}} \right)$$ (1) 式(1)中:q为试验计算炸药单耗,kg/m3;q′为初选炸药单耗,kg/m3;n为实际爆破漏斗作用指数.
校正后得到更为合适的炸药单耗q是0.981 kg/m3.
3 正交试验法优化扇形深孔的爆破参数
3.1 炮孔密集系数以及扇形深孔排距、孔底距优化
排距的大小对凿岩成本、爆破效果、回采进度和成本均有很大影响[4].小排距虽然能够改善爆破效果,但是降低了施工效率,增加了爆破成本,而排距过大则容易导致大块率高,甚至是出现“爆破墙”,严重影响爆破效果[5].炮孔的密集系数、排距、孔底距三者之间的关系式为:炮孔密集系数M=孔底距a/最小抵抗线W.
最小抵抗线的大小可根据经验公式计算,也可根据与扇形炮孔直径的关系,从相关矿山的实际资料中参考选取.
$$W = d\sqrt {7.85\frac{{\Delta \psi }}{{mq}}} $$ (2) 式(2)中:Δ为装药密度,kg/dm3;d为炮孔直径,dm;ψ为平均装药系数值;q为炸药单耗,kg/m3;m为炮孔密集系数.
3.2 扇形孔排距、孔底距试验方案
相同炸药单耗下,不同孔底距和排距爆破效果试验结果见表 2.
表 2 不同排距、孔底距布置矿得爆破效果编号 炸药单耗/(kg·m-3) 孔底距/m 排距/m 炮孔密集系数 大块率/% 1 0.981 1.9 1.5 1.27 2.5 1.9 1.6 1.19 2.8 1.9 1.7 1.12 3.2 1.9 1.8 1.06 3.5 1.9 1.9 1.00 4.1 2 0.981 2.0 1.5 1.33 2.7 2.0 1.6 1.25 2.6 2.0 1.7 1.18 3.2 2.0 1.8 1.11 3.5 2.0 1.9 1.05 3.9 3 0.981 2.1 1.5 1.40 2.6 2.1 1.6 1.31 2.5 2.1 1.7 1.24 2.6 2.1 1.8 1.17 3.1 2.1 1.9 1.11 3.9 4 0.981 2.2 1.5 1.47 2.5 2.2 1.6 1.38 2.4 2.2 1.7 1.29 2.6 2.2 1.8 1.22 3.1 2.2 1.9 1.16 3.8 5 0.981 2.3 1.5 1.53 3 2.3 1.6 1.44 3.5 2.3 1.7 1.35 3.8 2.3 1.8 1.28 4.2 2.3 1.9 1.21 4.4 由表 2的记录情况,可以发现当孔底距保持不变时,爆破后大块率与密集系数m成反比,当密集系数m保持在一定范围时,大块率与孔底距成正比关系.这是由于孔底距和排距都增大,导致孔网密度变稀,由于每个炮孔装药量一定,根据体积原理,在装药量没有改变情况下,爆破岩石体积增多,大块产出率必然随之增大.与此同时,由于是采用分段崩落法回采,在挤压崩落围岩的条件下爆破的落矿同样也增加了大块率.综合比较得出排距在1.6~1.85 m之间合理,孔底距在2~2.2 m之间合理.在此情况下,凿岩工程量大为减少,极大地加快了施工进度.爆破后,回采进路眉线保持平整,巷道掉块和片帮较少,后排炮孔变形破坏程度较轻,大块产出率也低[6-7].
3.3 崩矿步距的优化
崩矿步距是无底柱分段崩落采矿方法的重要落矿参数之一,由于该方法在覆岩下放矿,矿石损失贫化与崩矿步距之间具有很大的相关性.所以控制矿石的损失和贫化应该从爆破参数的优化和放矿方式的改进两方面来着手.
最佳崩矿步距可根据理论计算、数值模拟放矿、室内物理模拟放矿和现场工业性试验等方法来确定.当矿区回采巷道间距、分层高度都已确定,在采矿过程中很难再进行调整,而崩矿步距却不一样,可以随时进行灵活的调整.合理崩矿步距L是按三者最佳配合原则来确定,当三者最佳配合时回采效率能够达到最大,贫化率也较小,此时的崩矿步距为最佳值[8-9].通过理论计算并结合现场工业试验统计回收率与贫化率之差来确定最优的崩矿步距.
3.4 崩矿步距的理论计算
回采效率的表达式为:
$$\lambda = \frac{{{V^2}}}{{{V_{\rm{f}}}{V_{\rm{h}}}}}$$ (3) 式(3)中:λ为回采效率:Vh为混入废石体积;V为矿石体积;Vf为放出体体积.
放出的矿体在矿石脊平面的切割作用下,放出矿体体积Vf、矿石体积V与混入废石体积Vh,如图 1所示,有以下关系:
$$\begin{array}{l} {V_{\rm{f}}} = \frac{2}{3}{\rm{ \mathsf{ π} }}abc + {\rm{ \mathsf{ π} }}abc\frac{{a{\rm{tan}}\theta }}{{\sqrt {{a^{\rm{2}}}{\rm{tan}}\theta } + {{\rm{c}}^2}}}[1 - \frac{{{{(a\tan \theta )}^2}}}{{3({a^2}{{\tan }^2}\theta + {c^2})}}]\\ \;\;\;{V_{\rm{h}}} = {\rm{ \mathsf{ π} }}\mathit{abc}[2 - \frac{{L - a\tan \theta }}{{\sqrt {{a^2}{{\tan }^2}\theta + {c^2}} }}(1 - \frac{{{{(L - a\tan \theta )}^2}}}{{3({a^2}{{\tan }^2}\theta + {c^2})}}) - \\ \;\;\;\;\;\;\;\frac{{2M}}{{\sqrt {{a^2}{{\tan }^2}\theta } + {c^2}}}(1 - \frac{{{M^2}}}{{3({a^2}{{\tan }^2}\theta + {c^2})}})]\\ \;\;\;\;\;\;\;\;\;\;\;\;M = \frac{1}{{2(B - K)}} + (1 + H + a)\tan \varphi \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;V = {V_{\rm{f}}} - {V_{\rm{h}}} \end{array}$$ (4) 式(4)中:L为崩矿步距;θ一般取4.5°左右;φ一般在15°~20°;M为漏斗母线在Z轴方向上所截的线段长度;B为进路间距;K为回采进路宽;H为分段高度.
V是L的函数,将式(4)中各相关函数代入式(3)中并对L求一阶导数,求λ的极值,可得到回采效率最大时的崩矿步距为:
$$L = \frac{1}{{10}}[9a\tan \theta + \sqrt {81{a^2}{{\tan }^2}\theta + 60{c^2}} ]$$ (5) 化简后的崩矿步距表达式为:
$$L = a\tan \theta + 0.77c$$ (6) 由式(5)可知,求得长半轴a的值和纵短半轴c的值就可求得崩矿步距L.
$$\mathit{a} = \frac{{{k^2} + 4{H^2}_{\rm{f}}\left( {1 - {\varepsilon ^2}} \right)}}{{8{H_{\rm{f}}}\left( {1 - {\varepsilon ^2}} \right)}}$$ (7) $$\mathit{b} = \frac{{{k^2} + 4{H^2}_{\rm{f}}\left( {1 - {\varepsilon ^2}} \right)}}{{8{H_{\rm{f}}}\left( {1 - {\varepsilon ^2}} \right)}}$$ (8) $$\varepsilon = \frac{{\sqrt {{\mathit{a}^2}{\rm{ - }}{\mathit{b}^2}} }}{\mathit{a}}$$ (9) $${H_{\rm{f}}} = 2H - K$$ (10) 式(9)、式(10)中:Hf为放矿高度;ε为放出体偏心率.
将Hf为26 m,ε为0.93~0.95代入到式(7)、式(8)、式(9)可得:
a=13.57~13.79 m;b=4.31~6.3 m;c=4.13~6.09 m
将上述a、c和θ值代入到式(6)中,求得最佳崩矿步距为4.26~5.78 m.
根据上述理论计算最佳崩矿步距的结果,结合矿石的碎胀系数1.4,一次崩矿3排时正好在最佳崩矿步距理论计算的范围内.
3.5 正交工业试验确定崩矿步距
崩矿步距的试验要求与生产期具有相同的放矿环境[10],即在覆岩的条件下出矿,回采进路扇形孔孔底距均为2.1 m,回采进路中的扇形孔具有不同范围(1.6~1.85 m)的排间距.因此,工业试验布置在19#勘探线的回采进路中,放矿设计要求矿石回收率不低于75 %,贫化率不超过12 %.表 3为试验统计结果.
表 3 不同崩矿步距正交试验情况编号 排间距/m 崩矿间距/m 崩落矿量/t 出矿量/t 实际回收率/% 贫化率/% 回贫差/% 1 1.80 1.80 968.6 890 73.1 21.2 51.8 2 1.80 1.80 968.6 911 71.2 25.7 45.5 3 1.60 3.00 1 722.7 1 360 69.2 18.7 50.5 4 1.70 3.20 1 846.2 1 424 71.7 8.73 63.0 5 1.60 4.90 2 543.6 2 355 81.2 9.6 71.6 6 1.85 3.70 1 991.4 1 876 77.8 17.3 60.5 7 1.80 3.60 1 927.8 1 723 75.4 15.4 60.0 8 1.75 5.25 2 825.8 2 761 83.4 14.6 68.8 9 1.75 5.25 2 825.9 2 347 76.7 7.6 69.1 10 1.75 3.50 1 883.0 1 639 70.9 18.5 52.4 11 1.80 5.40 2 906.5 2 386 76.2 7.1 69.1 12 1.80 5.10 2 906.5 2 576 80.3 9.3 71.0 13 1.70 5.40 2 099.1 1 869 74.1 16.7 57.4 表 3中编号为第5、9、11、12组放出体在回收率和控制贫化方面都满足放矿要求,第8组放出体虽然回贫差较大,但是放矿时端部混入废石多导致贫化率高,没有达到设计的生产要求.总体来说崩矿步距为4.8~5.4 m,一次出矿量控制在2 400 t左右,矿石回收率和贫化率都较好,能够满足生产效率和经济效益要求.
正交试验表明当选择的最佳崩矿步距在4.8~5.4 m之间时,放出体的形态与爆破堆积体形态相对吻合,若加强放矿管理,能够有效改善矿石的损失和贫化率,提高原矿质量、满足生产实际要求[11-12].
4 结论
1)通过标准抛掷爆破漏斗试验能够较为准确地获得适合该矿区的炸药单耗值,经过计算炸药单耗选用0.981 kg/m3更为合适,运用正交试验来确定扇形孔的排距和孔底距是一种较为准确的方法,试验优化后的排距为1.6~1.85 m,孔底距为2~2.2 m.
2)根据放矿理论对20 m×15 m的间距情况下进行最佳崩矿步距的理论计算与不同崩矿步距放矿的工业试验.通过理论计算并结合现场工业试验统计回收率与贫化率之差来确定最优的崩矿步距,可以得出崩矿步距在4.8~5.4 m范围内为宜,小崩矿步距虽然能够增加矿石的回收,但是矿石贫化严重,容易形成悬顶,大崩矿步距虽然能够降低矿石贫化,但是端部矿体难以放出导致回收率低.
-
表 1 不同水口结构参数

-
[1] B.G. Thomas,L.J. Mika, F.M. Najjar. Simulation of fluid flow inside acontinuous slab casting machine[J]. Metall Trans B,1990,21(2):387. doi: 10.1007/BF02664206
[2] S. Hintikka, J. Konttinen, K. Leiviska. Optimization of molen steel flow in continuous casting mold[C] // Steelmaking Conference Proceedings,1992:887.
[3] 顾武安,唐萍,文光华,等.大方坯连铸四孔浸入式水口的应用研究[J].钢铁,2008,43(4):101-104. http://www.cnki.com.cn/Article/CJFDTOTAL-GANT200804025.htm [4] 王维维,张家泉,陈素琼,等.水口侧孔倾角对大方坯结晶器流场和液面波动的影响[J].北京科技大学学报,2007, 29(8):816-821. http://www.cnki.com.cn/Article/CJFDTOTAL-BJKD200708016.htm [5] 张胤,贺友多,白学军,等.水口插入深度对连铸机结晶器内钢液流动的影响[J].炼钢,2001,17(2):52-54. http://www.cnki.com.cn/Article/CJFDTOTAL-LGZZ200102016.htm [6] 高泽平,苏振江.大方坯连铸结晶器浸入式水口结构优化[J].炼钢,2008,24(2):42. http://www.cnki.com.cn/Article/CJFDTOTAL-LGZZ200802011.htm [7] 吴狄峰. 大方坯结晶器内钢液流动 、传热 、夹杂物运动及电磁制动研究[D]. 北京:北京科技大学,2008. [8] 李增玉,张彩军,关开,等. 异型坯结晶器内钢水流动和凝固过程的耦合数值模拟[J]. 江西冶金,2009,17(1):11-13. http://www.cnki.com.cn/Article/CJFDTOTAL-HNYE200901005.htm [9] 邓南阳,金友林. 304 不锈钢板坯连铸结晶器水口结构优化的数值模拟[J]. 特殊钢,2010,31(3):10-13. http://www.cnki.com.cn/Article/CJFDTOTAL-TSGA201003006.htm [10] 干勇,仇圣桃.连续铸钢过程数学物理模拟[M].北京 :冶金工业出版社,2001. [11] 孙海波,韩占光,钱宏智,等.注流方式对大方坯连铸结晶器内钢水流动与温度状态的影响 [J]. 北京科技大学学报,2010,32(9): 1131-1137. http://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201009005.htm [12] K. Frauenhuber. 奥钢联不锈钢连铸技术的最新发展 [J]. 钢铁,2001,36(4):27-30. http://cn.bing.com/academic/profile?id=120778863&encoded=0&v=paper_preview&mkt=zh-cn



 下载:
下载: